6. Neposedná lyžička vzorové riešenie

Ako vzorové riešenie sme použili riešenie Majka Kovaľa so zopár kozmetickými úpravami.

Marián Kovaľ
Gymnázium Grösslingová 18, Kvinta A
Príklad číslo 6

Keďže lyžička sa po miske hýbe bez trenia, sila je iba kolmá na povrch misky. Miska je rotačne symetrická okolo osi \(z\), horizontálna zložka normálovej sily, ktorou miska pôsobí na lyžičku bude iba v radiálnom smere – do stredu. Ak sa lyžička dotýka misky v dvoch bodoch (čo sa bude vždy, ak nebude vyvážená na jednom konci, čo je jedno z riešení), pôsobia na ňu dve sily v horizontálnom smere – od týchto dvoch bodov. Tieto dve sily sa musia odčítať, a teda musia pôsobiť v presne opačných smeroch. Keďže sila od misky pôsobí vždy presne smerom do stredu, konce lyžičky musia byť na opačných stranách od osi \(z\). Vezmem teda zvislý rez priestorom, ktorý obsahuje lyžičku aj stred misky. Viem, že žiadne sily nebudú vychyľovať lyžičku z tejto roviny, a teda mi stačí úlohu riešiť v 2D prípade, kde \(z = \frac{x^2}{2p}\). Lyžička bude v stabilnej polohe, keď výslednica síl aj momentov síl na ňu pôsobiacich bude nulová.

Viem, že ak posuniem sily v smere ich pôsobenia, nezmení sa ich efekt (celková sila ani moment sily). Môžem ich teda presunúť do jedného bodu a tam ich sčítať. Aby bola celková sila nulová, súčet síl od misky musí byť zvislý a rovný tiaži. Keďže táto sila je zvislá, môžem ju posúvať v zvislom smere. Aby bol moment sily nulový, táto sila by sa mala dať posunúť do ťažiska. To znamená, že aby bola situácia stabilná, musia sa \(x\)-ové zložky normály v koncoch lyžičky vynulovať.

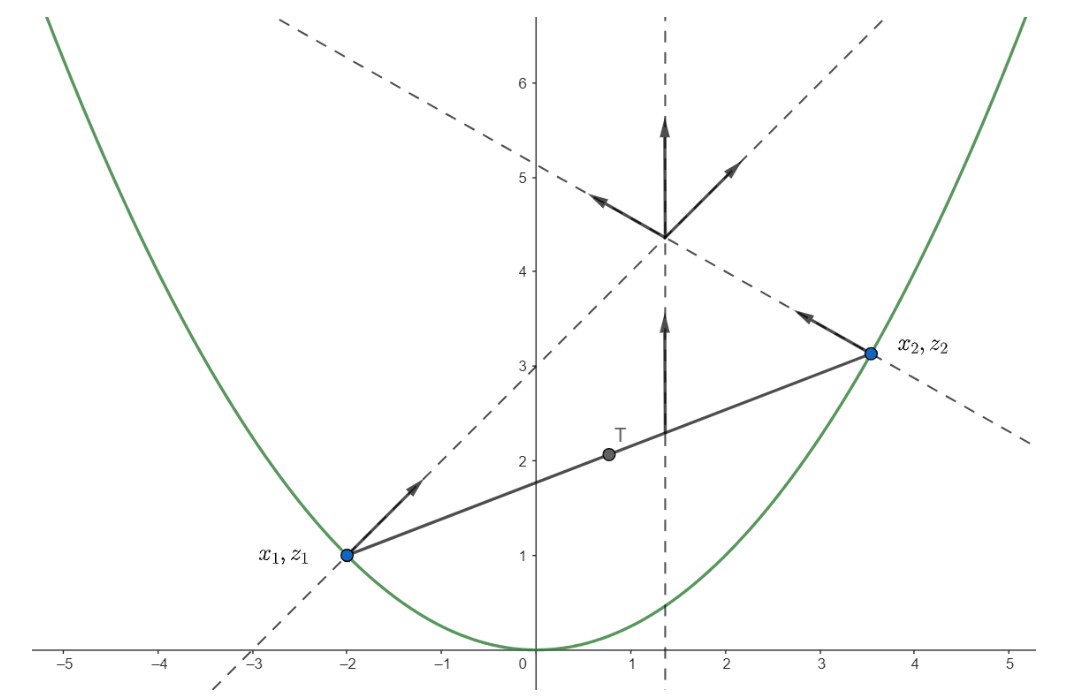
Normálové vektory sú kolmé na dotyčnicové vektory, takže ich viem vypočítať vypočítaním dotyčníc (derivácia tvaru nádoby je \(\frac{d}{dx} \frac{x^2}{2p} = \frac{x}{p}\)) a následným otočením o \(\ang{90}\). Ak sa lyžička dotýka misky v bode s \(x\)-ovou súradnicou \(x_1\), tak dotyčnicový vektor tam je \[ \vec{t_1} = \left(1, \frac{x_1}{p}\right) \] a normálový teda je \[ \vec{n_1} = \left(-\frac{x_1}{p}, 1\right). \] V druhom bode dotyku je analogicky¹ \[ \begin{aligned} \vec{t_2} &= \left(1, \frac{x_2}{p}\right), \\ \vec{n_2} &= \left(-\frac{x_2}{p}, 1\right). \end{aligned} \]

Z toho vieme zistiť rovnice priamok, na ktorých ležia normálové sily, konkrétne \[ (x - x_1) = \left(z - z_1\right) \left(-\frac{x_1}{p}\right) \] a \[ (x - x_2) = \left(z - z_2\right) \left(-\frac{x_2}{p}\right). \]

Keď vyriešim tieto rovnice pre \(x\) a \(y\), pričom \(x\) bude rovné \(\frac{x_1 + x_2}{2}\), znamená to, že tieto sily sa sčítajú do ťažiska. Takže \[ \begin{aligned} x + z \frac{x_1}{p} = x_1 \left(1 + \frac{z_1}{p}\right), \\ x + z \frac{x_2}{p} = x_2 \left(1 + \frac{z_2}{p}\right). \end{aligned} \qquad(1)\]

Odčítam druhú rovnicu od prvej \[ z \frac{x_1 - x_2}{p} = x_1 \left(1 + \frac{z_1}{p}\right) - x_2 \left(1 + \frac{z_2}{p}\right) \] a vyjadrím \[ z = \left[x_1 \left(1 + \frac{z_1}{p}\right) - x_2 \left(1 + \frac{z_2}{p}\right)\right] \frac{p}{x_1 - x_2} = \frac{x_1(p + z_1) - x_2(p + z_2)}{x_1 - x_2}. \]

Teraz to dosadíme naspäť do rovnice 1, čím odstávame \[ x + \frac{x_1(p + z_1) - x_2(p + z_2)}{x_1 - x_2} \frac{x_1}{p} = x_1 \left(1 + \frac{z_1}{p}\right). \] Vyjadrím \[ \begin{aligned} x &= x_1 \left(1 + \frac{z_1}{p}\right) - \frac{x_1(p + z_1) - x_2(p + z_2)}{x_1 - x_2} \frac{x_1}{p}, \\ &= - \frac{x_1 x_2 (z_1 - z_2)}{p (x_1 - x_2)}, \\ &= - \frac{x_1 x_2 \left(\frac{x_1^2}{2p} - \frac{x_2^2}{2p}\right)}{p (x_1 - x_2)}, \\ &= - \frac{x_1 x_2 (x_1 + x_2) (x_1 - x_2)}{2p^2 (x_1 - x_2)}, \\ &= - \frac{x_1 x_2 (x_1 + x_2)}{2p^2}. \end{aligned} \]

Na to, aby situácia bola stabilná, \(x\) sa musí rovnať \(\frac{x_1 + x_2}{2}\). Tak napíšem rovnicu: \[ \begin{aligned} x &= - \frac{x_1 x_2 (x_1 + x_2)}{2p^2} = \frac{x_1 + x_2}{2}, \\ \frac{x_1 x_2}{p^2} &= -1, \\ x_2 &= - \frac{p^2}{x_1}. \end{aligned} \qquad(2)\]

Teraz sa dá vyjadriť dĺžka lyžičky z \(x_1\) – ja si však vyjadrím namiesto toho jej druhú mocninu, aby som tam nemal odmocniny: \[ l^2 = (x_1 - x_2)^2 + (z_1 - z_2)^2 = \left(x_1 + \frac{p^2}{x_1}\right)^2 + \left(\frac{x_1^2}{2p} - \frac{\frac{p^4}{x_1^2}}{2p}\right). \]

Po úprave dostaneme \[ l^2 = \frac{(p^2 + x_1^2)^4}{4p^2 x_1^4}. \] Dĺžka je vždy kladná, teda \[ l = \frac{(p^2 + x_1^2)^2}{2p x_1^2}. \]

Označme si \(x_1^2\) ako \(k\), a vznikne nám kvadratická rovnica \[ 2plk = p^4 + 2p^2 k + k^2, \] ktorej riešením je \[ k = x_1^2 = \frac{2p(l - p) \pm \sqrt{4p^2(p - l)^2 - 4p^4}}{2} = p \left(l - p \pm \sqrt{(l - p)^2 - p^2}\right). \]

Odmocnením získame \(x_1\). Mohli by sme pridať aj \(\pm\), ale to tam bude triviálne, keďže situácia je symetrická podľa osi \(y\), takže \[ x_1 = \sqrt{p \left(l - p \pm \sqrt{(l - p)^2 - p^2}\right)}. \] Hodnota \(z_1\) je daná rovnicou tvaru misky, čiže poznáme súradnice jedného bodu, kde sa lyžička dotýka misky. Ohľadom druhého bodu, hodnotu \(x_2\) vypočítame z rovnice 2, a potom \(z_2\) je opäť dané tvarom misky.

Toto je len jedným z riešení. Ďalšie riešenie, ktoré z týchto rovníc nevypadne je, že \(x_1 = -x_2 = \frac{l}{2}\), čiže lyžička je vodorovne. Toto riešenie z tohto odvodenia nevyplynie preto, že v istom momente som delil \(x_1 + x_2\), čo sa teda v takom prípade nedá. Ďalšie riešenie, ktoré popiera predpoklad, že sa dotýka v dvoch bodoch, je riešenie, pri ktorom je lyžička v strede misky vyvážená na jednom svojom konci. Ostatné predpoklady, ktoré som urobil už triviálne vždy platia.