Zadanie

Kvík sa pripravuje na dušičky, a preto začal cvičiť zapaľovanie sviečok. Pritom si všimol, že zápalka môže horieť rôzne rýchlo, podľa toho ako ju drží. Odmerajte, ako rýchlo horí zápalka1 v závislosti od jej naklonenia voči zvislému smeru.

Pri riešení tejto úlohy nezabudnite dodržiavať zásady práce s otvoreným ohňom.

  1. napríklad v \(\si{\milli\metre\per\second}\)↩︎

Ako vzorové uvádzame veľmi pekné riešenie od Anny Oleárovej.

Aparatúra

  1. dlhé zápalky
  2. zapaľovač
  3. uhlomer
  4. zemiak
  5. stabilne uchytený telefón
Aparatúra

Metodológia experimentov

  1. Na stenu som prilepila uhlomer, pred ten som na stôl položila zemiak tak, aby bol v strede uhlomera. Podľa toho som nastavila aj telefón s kamerou. Hodnotu \(\ang{0}\) som si určila v smere kolmo nahor. (Na fotkách s kladnými hodnotami bol síce uhlomer otočený o \(\ang{90}\), pri spracúvaní údajov boli hodnoty ale upravené a počítané správne, podľa mnou určenej vertikálnej osi.)
  2. Do zemiaka som zapichla dlhú zápalku vždy do hĺbky okolo \(\SI{5}{\milli\metre}\). Keď nastali uhly väčšie ako \(\ang{90}\), zemiak som napichla na palicu, ktorú som uistila drevom, aby sa nehýbala. Zemiak vytŕčal zo stola, a preto bolo možné zapichnúť zápalku aj v týchto uhloch.
  3. Vždy som zápalku zapálila zapaľovačom.
  4. Pokusy som robila s rozostupmi po \(\ang{10}\) a vždy trikrát, čo robí dokopy 57 videí.
Aparatúra

Metodológia spracúvania údajov

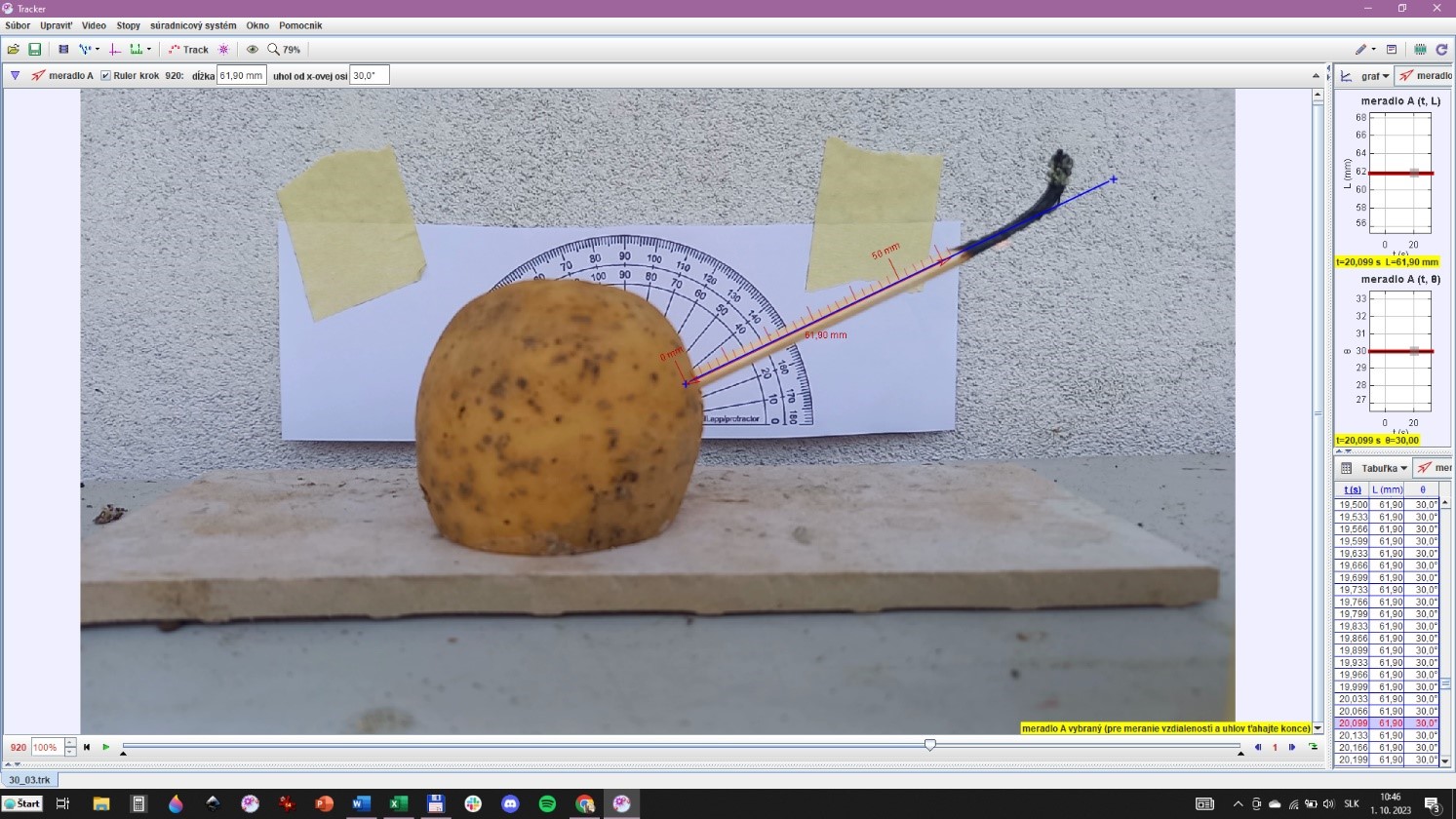
  1. Videá som spracúvala v programe Tracker.
  2. Ako referenčnú škálu som použila zápalku. Zápalka bola zapichnutá \(\SI{5}{\milli\metre}\) v zemiaku, jej hlavička má cca \(\SI{10}{\milli\metre}\) na dĺžku, a celá zápalka má dĺžku \(\SI{100}{\milli\metre} \pm \SI{2}{\milli\metre}\) (hodnoty podľa balenia).
  3. Čas horenia som určovala od momentu, kedy prestane horieť iba hlavička a chytí sa aj samotná drevená časť zápalky, nakoľko hlavička horí pri všetkých uhloch rýchlosťou s minimálnym rozdielom, lebo celá vzplanie naraz. Kebyže do času započítam aj horenie hlavičky, čas by bol mierne dlhší, ale u všetkých uhlov rovnako. Prišlo mi preto také objektívnejšie dávať hodnoty už ustáleného plameňa.
  4. Čo sa týka dĺžky, nemerala som priamo zošúverenú spálenú časť, ale od \(\SI{85}{\milli\metre}\) (= \(\SI{100}{\milli\metre}\) celej dĺžky – \(\SI{5}{\milli\metre}\) zo zapichnutia – \(\SI{10}{\milli\metre}\) z hlavičky) som odčítala dĺžku nespálenej zápalky v \(\si{\milli\metre}\).
  5. Potom som vypočítala rýchlosť nasledovným vzorcom: \[ \text{rýchlosť horenia}[\si{\milli\metre\per\second}] = \frac{\text{dĺžka spálenej zápalky} [\si{\milli\metre}]}{\text{čas horenia} [\si{\second}]}. \]
  6. Rýchlosti z troch meraní som spriemerovala. Chybové úsečky \(y\)-ovej osi (teda nepresnosti pri rýchlosti) sú tvorené rozdielom medzi najvyššou a najnižšou rýchlosťou z troch meraní a spriemerovanej rýchlosti. Chybové úsečky \(x\)-ovej osi (teda nepresnosti pri uhloch) som si sama určila na \(\ang{2.5}\) alebo \(\SI[parse-numbers=false]{\frac{\pi}{72}}{\radian} = \SI{0.0436}{\radian}.\)
Aparatúra

Keď som skúsila merania fitnúť polynomiálnym trendom druhého stupňa, rovnica spoľahlivosti bola \(\num{0.954}\). Táto hodnota nie je úplne \(1\), ale to je odôvodniteľné odchýlkami v meraní (popísané nižšie). Pekne sedel aj fit exponenciálny s rovnicou spoľahlivosti o hodnote \(\num{0.912}\). Fitujeme len polovicu možných uhlov, lebo druhá polovica je symetrická. Je to v podstate to isté, akoby som kameru otočila voči zemiaku so zápalkou opačne a horela by stále v rovnakých hodnotách. Je to osovo súmerné.1

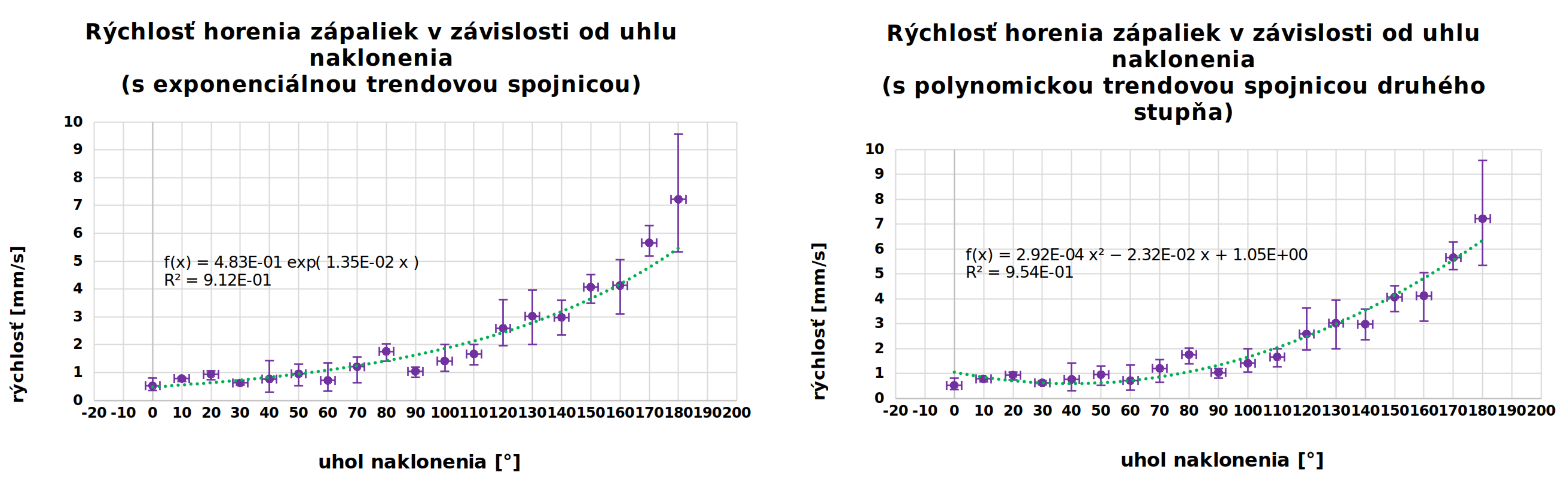
Namerané hodnoty vynesené do grafov.

Kvalitatívne vysvetlenie

Tento trend má celkom dobré kvalitatívne vysvetlenie. Keďže plameň stúpa nahor, je pochopiteľné, že keď sa nachádzame v uhloch väčších ako \(\ang{90}\) (kedy je nad hlavičkou smerom nahor zvyšok zápalky – drevená časť), tak sa plameň chytí o drevo nad horiacou hlavičkou. Z tohto dôvodu aj všeobecne horeli zápalky v týchto uhloch dlhšiu vzdialenosť. Častokrát zhorela aj celá zápalka, čo sa pri uhloch menších ako \(\ang{90}\) nestávalo skoro vôbec.

Rozdiel horenia zápalky pri rôznych uhloch

Analýza chýb merania

Dôvodov, prečo výsledky sú nie úplne presné, môže byť viacero:

  1. zápalka zapichnutá pod nepresným uhlom (\(\pm \ang{2.5}\))
  2. zápalka zapichnutá do nepresnej hĺbky (cca \(\SI{5}{\milli\metre}\))
  3. neidentické zápalky
  4. nedostatočné množstvo opakovaní experimentov
  5. nepresne nalepený uhlomer
  6. efekty prúdenia vzduchu v lokalite točenia
  7. nepresné určenie začiatku horenia drevenej časti zápalky

Všetkým týmto chybám som sa snažila vyhnúť viacnásobnou kontrolou, či sa nevyskytli. Samozrejme je ale možné a isté, že nejaké sa predsa len vyskytli a ovplyvnili výsledky.

  1. Je dôležité podotknúť, že v tomto prípade ani jedna z fitovaných funkcii nie je podložená žiadnou teóriou. Z toho dôvodu fitované funkcie nemôžeme považovať za fyzikálne relevantné závislosti, ale iba prostriedok na odhadnutie hodnôt medzi meranými bodmi. Táto skutočnosť je viditelná aj na zásadnej odchylke funkcii a reálnych hodnôt na koncoch grafov. Fitované funkcie majú preto skôr význam, aby sme si uvedomili, že pravdepodobne nepôjde o žiadnu jednoduchú závislosť.↩︎

Diskusia

Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.

Pre pridávanie komentárov sa musíš prihlásiť.