7. Pomocník s hadicou vzorové riešenie

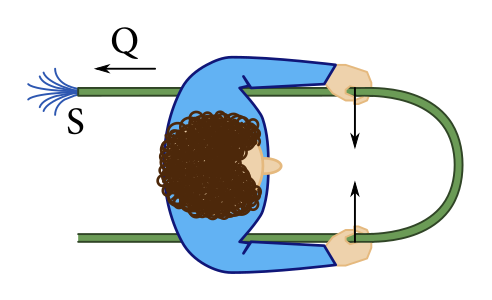
Zo zadania vieme, že hadica má prierez \(S\) a voda v hadici má prietok \(Q\). Odtiaľ je rýchlosť prúdenia vody v hadici \(v = \frac{Q}{S}\).

Uvažujme krátky kúsok hadice prislúchajúci stredovému uhlu \(\delta\phi\). V takomto kúsku hadice sa v každom momente nachádza voda s hmotnosťou \(\delta m = \varrho SR\delta\phi\). Nájdime, akou silou na ňu hadica pôsobí. Najjednoduchšie to urobíme tak, že si uvedomíme, že sila od hadice je dostredivou silou pre túto vodu, preto \[ \delta F = F_{\mathrm{dostr}} = \delta m\frac{v^{2}}{R} = \varrho Sv^{2}\delta\phi. \]

Vidíme, že táto sila závisí na veľkosti stredového uhla lineárne. Označme si preto silu normovanú na jednotkový uhol ako \[ f = \frac{\delta F}{\delta\phi} = \varrho Sv^{2} = \frac{\varrho Q^{2}}{S}. \]

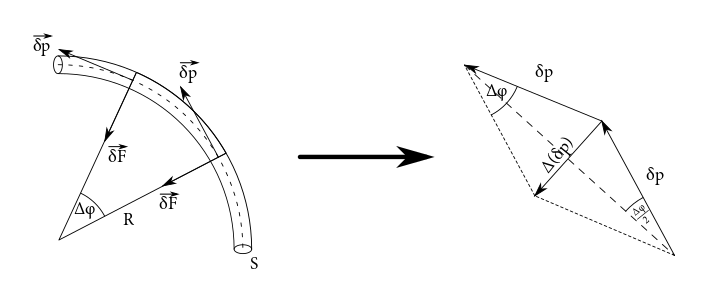
Túto silu vieme dostať aj iným, mierne pracnejším spôsobom. Pri jej odvodzovaní však nájdeme dôležitý medzivýsledok, ktorý sa nám zíde neskôr, preto si ukážme aj tento druhý spôsob. Uvažujme opäť element vody v hadici prislúchajúci stredovému uhlu \(\delta\phi\). Jeho hybnosť je \[ \delta p = \delta m v = \varrho SR\delta\phi v = \varrho QR\delta\phi \] a hybnosť prislúchajúca jednotkovému uhlu \[ q = \frac{\delta p}{\delta\phi} = \varrho QR. \]

Za čas \(\Delta t\) sa element vody posunie do vzdialenosti \(v\Delta t\) a tejto vzdialenosti zodpovedá zmena stredového uhla \(\Delta\phi = \frac{v\Delta t}{R}\). Veľkosť hybnosti elementu vody sa pritom nijako nezmení, zmení sa len jej smer. Hybnosť ako vektor sa teda zmení. Zmenu hybnosti jednoducho nájdeme využitím jednoduchej geometrie ako dĺžku uhlopriečky kosoštvorca (viď fig. 1) ako \[ \Delta\left(\delta p\right) = 2\delta p\sin\left(\frac{\Delta\phi}{2}\right) \approx 2\delta p\frac{\Delta\phi}{2} = \varrho QR\delta\phi\frac{v\Delta t}{R} = \frac{\varrho Q^{2}}{S}\delta\phi\Delta t. \]

Konečne podľa druhého Newtonovho zákona sila je rovná zmene hybnosti za čas, preto \[ \delta F = \frac{\Delta\left(\delta p\right)}{\Delta t} = \frac{\varrho Q^{2}}{S}\delta\phi, \] čo je identický výsledok, ako sme dostali pri výpočte cez dostredivú silu.

Podľa tretieho Newtonovho zákona element vody pôsobí na jemu prislúchajúci kúsok hadice rovnako veľkou silou opačného smeru. Aby bola hadica v rovnováhe, musí byť výsledná sila na ňu pôsobiaca nulová. Stačí nám teda sčítať príspevky od všetkých elementov vody v hadici a mali by sme mať vybavené. Poďme teda na to.

Chceme sčítať veľmi veľa veľmi malých príspevkov. To zaváňa integrovaním. Nevieme sa mu však nejako vyhnúť? Vieme! Vieme, že voda vytekajúca z hadice má opačný smer než voda do nej vtekajúca. Oblúk hadice teda mení hybnosť každého elementu vody z \(\delta p\) na \(-\delta p\), teda o \(-2\delta p\). Za čas \(\Delta t\) vtečie do hadice voda s hybnosťou \(\delta p = q\frac{v\Delta t}{R} = \frac{\varrho Q^{2}}{S}\Delta t\). Zmena hybnosti vody za tento čas je teda \(\Delta p = -2\delta p = -2\frac{\varrho Q^{2}}{S}\Delta t\) a sila, ktorou musí Patrik pôsobiť, je \[ F_{\parallel} = \frac{\Delta p}{\Delta t} = -2\frac{\varrho Q^{2}}{S}. \]

Táto sila sa rovnomerne rozkladá medzi jeho dve ruky, preto každou z nich musí pôsobiť silou \(\frac{F_{\parallel}}{2}\).

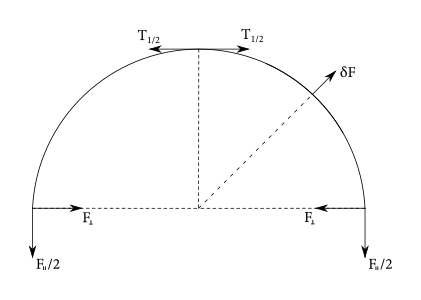
No dobre, toto je sila v smere vystretej časti hadice. Ale čo sila v smere kolmom na rovnú časť hadice? V tomto smere sa hybnosť nemení. Znamená to však, že aj sila je nulová? Keď sa pozrieme na nejaký kratší úsek polkružnicovej časti hadice, napríklad polovicu z nej, vidíme, že tu sa hybnosť vody na tomto úseku mení. Niekomu by mohlo napadnúť sčítať zložky sily pôsobiacej na hadicu od vody v tomto smere. Buď integrovaním alebo opäť jednoduchou úvahou o zmene hybnosti vody v štvrťkružnici zistíme, že na vodu v štvrťkružnici v kolmom smere musí pôsobiť sila \[ F_{\perp} = \frac{\varrho Q^{2}}{S}. \]

Je však toto sila, ktorou musí Patrik pôsobiť na hadicu v kolmom smere? Na prvý pohľad to tak vyzerá, no nemusí to tak byť. Platí totiž, že aby bolo teleso v rovnováhe, musí byť výslednica všetkých naň pôsobiacich vonkajších síl nulová. Lenže tým, že sme uvažovali len polovicu zakrivenej časti hadice, sme ju akoby rozrezali na polovicu a sila od druhej polovice hadice je teda tiež vonkajšou silou. Správne tvrdenie je teda, že \[ F_{\perp} + T_{\frac{1}{2}} = \frac{\varrho Q^{2}}{S}. \] No a o sile od druhej časti hadice zatiaľ nič povedať nevieme.

Stále sme však nevyužili druhú podmienku rovnováhy – nulovosť celkového momentu pôsobiacich síl. Pozrime sa teda na ňu. Za referenčný bod si zvoľme stred krivosti hadice. Vzhľadom na tento bod sú momenty síl od každého elementu kvapaliny v hadici nulové. Jedinými nenulovými momentmi sú moment od rovnobežnej zložky Patrikovej sily a moment sily od druhej polovice hadice. Matematicky zapísané \[ \frac{F_{\parallel}}{2}R + T_{\frac{1}{2}}R = 0. \]

Odtiaľ \[ T_{\frac{1}{2}} = -\frac{F_{\parallel}}{2} = \frac{\varrho Q^{2}}{S}. \] a teda \[ F_{\perp} = \frac{\varrho Q^{2}}{S} - T_{\frac{1}{2}} = 0. \]

Tento výsledok vyzerá dosť neintuitívne. Až tak, že by sme mohli začať pochybovať o tom, či je vôbec správny. Presvedčme sa o jeho správnosti teda ešte tak, že sa pozrieme na napäťové sily v hadici. Zadanie hovorí, že hadica je dokonale ohybná. To znamená, že napäťové sily v hadici majú v každom bode smer dotyčnice k hadici.

Uvažujme oblúk hadice prislúchajúci stredovému uhlu \(\Delta\phi\). Na jeden koniec tohto kúsku hadice pôsobí ťahová sila \(T\left(\phi-\frac{\Delta\phi}{2}\right)\), na druhý koniec ťahová sila \(T\left(\phi + \frac{\Delta\phi}{2}\right)\) (viď fig. 3). Tieto sily neležia na jednej priamke v dôsledku zakrivenia kúska hadice. Nájdime zložky ťahových síl v smere kolmom na os uhla \(\Delta\phi\). Tieto zložky musia byť v rovnováhe.¹ Dostávame \[ T\left(\phi - \frac{\Delta\phi}{2}\right)\cos\left(\frac{\Delta\phi}{2}\right) = T\left(\phi + \frac{\Delta\phi}{2}\right)\cos\left(\frac{\Delta\phi}{2}\right), \] odkiaľ \[ T\left(\phi - \frac{\Delta\phi}{2}\right) = T\left(\phi + \frac{\Delta\phi}{2}\right). \] Táto rovnica hovorí, že napäťová sila o kúsok ďalej je rovnaká ako napäťová sila o kúsok skôr. To znamená, že napäťová sila je všade rovnaká \[ T\left(\phi\right) = \mathrm{konšt.} \]

My však vieme, že na začiatku polkružnice je napäťová sila daná silou, ktorou Patrik ťahá za hadicu \[ \left.T\left(\phi\right)\right|_{\phi = 0} \equiv T_{0} = \frac{F_{\parallel}}{2} = \frac{\varrho Q^{2}}{S}. \]

No a keďže má byť napäťová sila pozdĺž celej hadice rovnaká, tak aj v strede oblúka musí byť \[ T_{\frac{1}{2}} \equiv \left.T\left(\phi\right)\right|_{\phi = \frac{\pi}{2}} = \left.T\left(\phi\right)\right|_{\phi = 0} = \frac{\varrho Q^{2}}{S}. \] Toto je konzistentné s naším výsledkom.

Uvedomme si, že ak je hadica dokonale ohybná, tak nie je schopná hromadiť strižné napätia (t. j. napätia kolmé na hadicu). Inými slovami, ak by Patrik pôsobil silou v smere kolmom na hadicu, tak absencia strižných napätí by znamenala, že by neexistovala sila od zvyšku hadice, ktorá by bránila kúsku hadice v Patrikovej ruke v pohybe a hadica by nadobudla taký tvar, aby smer sily, ktorú vyvíja Patrik, bol dotyčnicou k hadici. Potom by už zvyšok hadice dokázal kompenzovať Patrikovo pôsobenie ťahovou silou v smere hadice.

Ak máte ešte stále problém tento výsledok pochopiť, predstavte si, že hadicu nedrží Patrik, ale že presne v miestach, kde začína a končí oblúk, sú uviazané špagáty, na ktorých hadica visí tesne nad zemou. Oblúk hadice má pochopiteľne rovnaký tvar, ako keď ju držal Patrik. Nič sa nezmenilo, len spôsob jej uchytenia. Teraz je však jednoduchšie nahliadnuť, že sila musí pôsobiť len v smere špagátu, pretože ten zjavne nie je schopný vyvinúť silu kolmú na jeho smer. No a ak špagát dokáže udržať hadicu v požadovanom tvare aj bez sily v kolmom smere, nie je dôvod, aby to nedokázal aj Patrik.

Reálna hadica kladúca odpor pri ohybe²

V prípade dokonale ohybnej hadice sme dostali zaujímavý výsledok, a to, že nie je potrebná sila v kolmom smere na to, aby sme boli schopní udržať hadicu v požadovanom tvare. Na mieste je otázka, či toto platí všeobecne, alebo je to pravda len pre uvedený špecifický prípad. Prvotné výpočty³ naznačujú, že by to tak mohlo byť, no preskúmajme to ešte cez napäťové sily v hadici.

Požiadavka na dokonalú ohybnosť hadice sa do zadania dostala preto, aby sme neuvažovali silu potrebnú na ohyb samotnej hadice. Hneď na úvod povedzme, že toto nebudeme adresovať ani teraz. To, čo nás bude zaujímať, je, o koľko väčšou silou musí Patrik na hadicu pôsobiť v kolmom smere oproti situácii, keď ňou netečie voda. Alternatívne sa na to môžeme pozerať tak, že hadica má prirodzene tvar polkružnice v nenapätom stave, a teda nás zaujíma sila, ktorou musíme na ňu pôsobiť, aby sme ju v tomto tvare udržali, keď ňou začne prúdiť voda.

Táto situácia je už o čosi komplikovanejšia než predchádzajúca, preto k nej pristúpime systematickejšie. Zaveďme si kartézsku súradnicovú sústavu s počiatkom v strede krivosti hadice, s \(x\)-ovou osou v smere kolmom na rovnú časť hadice a \(y\)-ovou osou v smere rovnobežnom. Uhol \(\phi\) budeme merať od kladnej \(x\)-ovej polosi v ACW smere a komponenty síl budú kladné v smere doprava a nahor.

Uvažujme opäť oblúk hadice prislúchajúci stredovému uhlu \(\Delta\phi\). Na jeho konce opäť pôsobia napäťové sily od zvyšku hadice. Tentokrát ale môžu mať všeobecný smer. Budeme si ich preto rozpisovať po kartézskych zložkách. Zároveň silu pôsobiacu na koniec prislúchajúci menšiemu uhlu \(\phi\)⁴ budeme označovať horným indexom „-“ a silu pôsobiacu na opačný koniec horným indexom „+“, pričom zrejme platí \(T^{-}\left(\phi\right) = -T^{+}\left(\phi\right)\).⁵

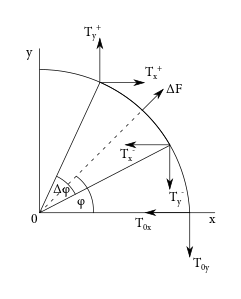
V rovnovážnom stave má byť výslednica síl pôsobiacich na každý kúsok hadice nulová. Zapíšme si teda rovnice rovnováhy síl po zložkách.

V \(x\)-ovom smere máme⁶ \[ T_{x}^{-}\left(\phi - \frac{\Delta\phi}{2}\right) + \Delta F_{x}\left(\phi\right) + T_{x}^{+}\left(\phi+\frac{\Delta\phi}{2}\right) = 0. \] Silu od kvapaliny poznáme \[ \Delta F_{x}\left(\phi\right) = \Delta F\left(\phi\right)\cos\phi = f\Delta\phi\cos\phi = \frac{\varrho Q^{2}}{S}\cos\phi\Delta\phi. \]

Po dosadení do predchádzajúcej podmienky a miernom preusporiadaní dostávame \[ \frac{T_{x}^{+}\left(\phi + \frac{\Delta\phi}{2}\right) - T_{x}^{+}\left(\phi - \frac{\Delta\phi}{2}\right)}{\Delta\phi} = -\frac{\varrho Q^{2}}{S}\cos\phi. \]

Na ľavej strane rovnice spoznávame deriváciu \(\frac{\mathrm{d}T_{x}^{+}\left(\phi\right)}{\mathrm{d}\phi}\). Získavame teda diferenciálnu rovnicu pre zložku \(T_{x}^{+}\left(\phi\right)\), ktorú však vieme vyriešiť jednoduchým integrovaním. Jej všeobecným riešením je \[ T_{x}^{+}\left(\phi\right) = -\frac{\varrho Q^{2}}{S}\sin\phi + C_{x}. \]

Konštantu \(C_{x}\) určíme z okrajových podmienok. Ak Patrik pôsobí na hadicu na začiatku polkružnice silou veľkosti \(T_{0x}\geq0\) vo vodorovnom smere, tak \[ \left.T_{x}^{-}\left(\phi\right)\right|_{\phi = 0} = -T_{0x} = -\left.T_{x}^{+}\left(\phi\right)\right|_{\phi = 0}, \] čiže \[ \left.T_{x}^{+}\left(\phi\right)\right|_{\phi = 0} = T_{0x}. \]

Zároveň vieme z našich predchádzajúcich úvah pre štvrťkružnicu, rešpektujúc našu znamienkovú konvenciu, že \[ \left.T_{x}^{-}\left(\phi\right)\right|_{\phi = 0} + \left.T_{x}^{+}\left(\phi\right)\right|_{\phi = \frac{\pi}{2}} = -\frac{\varrho Q^{2}}{S}. \]

Odtiaľ \[ \left.T_{x}^{+}\left(\phi\right)\right|_{\phi = \frac{\pi}{2}} = -\frac{\varrho Q^{2}}{S} + T_{0x}. \]

Z uvedených okrajových podmienok dostávame, že \[ C_{x} = T_{0x}. \]

Analogicky v \(y\)-ovom smere máme podmienku pre rovnováhu síl \[ T_{y}^{-}\left(\phi - \frac{\Delta\phi}{2}\right) + \Delta F_{y}\left(\phi\right) + T_{y}^{+}\left(\phi+\frac{\Delta\phi}{2}\right) = 0. \]

Tú vieme previesť na tvar \[ \frac{T_{y}^{+}\left(\phi + \frac{\Delta\phi}{2}\right) - T_{y}^{+}\left(\phi - \frac{\Delta\phi}{2}\right)}{\Delta\phi} = -\frac{\varrho Q^{2}}{S}\sin\phi. \]

Na ľavej strane opäť spoznávame deriváciu \(\frac{\mathrm{d}T_{y}^{+}\left(\phi\right)}{\mathrm{d}\phi}\), čiže získavame jednoduchú diferenciálnu rovnicu pre \(T_{y}^{+}\left(\phi\right)\). Jej všeobecné riešenie získané prostým integrovaním je \[ T_{y}^{+}\left(\phi\right) = \frac{\varrho Q^{2}}{S}\cos\phi + C_{y}. \]

Konštantu \(C_{y}\) určíme opäť z okrajových podmienok. Vieme, že Patrik pôsobí na hadicu v \(y\)-ovom smere silou veľkosti \(T_{0y} = \frac{\varrho Q^{2}}{S}\), teda \[ \left.T_{y}^{-}\left(\phi\right)\right|_{\phi = 0} = -\frac{\varrho Q^{2}}{S} = -\left.T_{y}^{+}\left(\phi\right)\right|_{\phi = 0}. \]

Zároveň na základe úvah o rozrezaní zo symetrie vyplýva, že \[ \left.T_{y}^{+}\left(\phi\right)\right|_{\phi = \frac{\pi}{2}} = \left.T_{y}^{-}\left(\phi\right)\right|_{\phi = \frac{\pi}{2}} = 0. \]

Zisťujeme, že integračná konštanta \[ C_{y} = 0. \]

Zistili sme, ako sa mení napäťová sila v hadici, tak si to zhrňme: \[ \begin{aligned} T_{x}^{-}\left(\phi\right) &= -T_{0x} + \frac{\varrho Q^{2}}{S}\sin\phi & T_{x}^{+}\left(\phi\right) &= T_{0x}-\frac{\varrho Q^{2}}{S}\sin\phi\\ T_{y}^{-}\left(\phi\right) &= -\frac{\varrho Q^{2}}{S}\cos\phi & T_{y}^{+}\left(\phi\right) &= \frac{\varrho Q^{2}}{S}\cos\phi \end{aligned} \]

Nepodarilo sa nám však určiť hľadanú silu \(T_{0x}\). Na to potrebujeme ešte použiť podmienku rovnováhy momentov síl. Poďme na to!

Momenty budeme počítať vzhľadom na počiatok súradnicovej sústavy. Polohový vektor sily prislúchajúcej uhlu \(\phi\) je \(\vec{r}\left(\phi\right) = \begin{pmatrix}R\cos\phi; & R\sin\phi\end{pmatrix}\). Moment ľubovoľnej sily \(\vec{F}\) vypočítame ako \(\vec{M} = \vec{r}\times\vec{F}\). V skutočnosti nás bude zaujímať iba jeho \(z\)-ová zložka \(M_{z} = xF_{y} - yF_{x}\). Pre uvažovaný kúsok hadice dostávame \[ \begin{aligned} -R\cos\left(\phi - \frac{\Delta\phi}{2}\right) \frac{\varrho Q^{2}}{S} \cos\left(\phi - \frac{\Delta\phi}{2}\right) - R\sin\left(\phi - \frac{\Delta\phi}{2}\right) \left[-T_{0x} + \frac{\varrho Q^{2}}{S}\sin\left(\phi - \frac{\Delta\phi}{2}\right)\right] &+ \\ +R\cos\left(\phi + \frac{\Delta\phi}{2}\right) \frac{\varrho Q^{2}}{S} \cos\left(\phi + \frac{\Delta\phi}{2}\right) - R\sin\left(\phi + \frac{\Delta\phi}{2}\right) \left[+T_{0x} - \frac{\varrho Q^{2}}{S}\sin\left(\phi + \frac{\Delta\phi}{2}\right)\right] &= 0. \end{aligned} \]

Po pár úpravách konečne zisťujeme, že \[ T_{0x} = 0. \]

Tým sme si potvrdili, že ani v prípade reálnej hadice nemusí Patrik vynakladať dodatočnú silu v kolmom smere na rovnú časť hadice v súvislosti s prúdením vody v hadici.

Poznajúc silu, ktorou Patrik pôsobí na hadicu, vráťme sa ešte na chvíľu k priebehu napäťových síl v hadici. Môžeme si všimnúť, že hoci zložky napäťových síl \(T_{x}\left(\phi\right)\) a \(T_{y}\left(\phi\right)\) závisia na uhle, veľkosť napäťovej sily vypočítaná podľa Pytagorovej vety \(T = \frac{\varrho Q^{2}}{S}\) na uhle nezávisí, čiže je všade rovnaká. Zároveň skalárny súčin \(\vec{r}(\phi) \cdot \vec{T}\left(\phi\right) = 0\), čo znamená, že napäťová sila je kolmá na polomer, a teda má smer dotyčnice k hadici. Takže hoci sme pripustili, že by napäťová sila mohla mať ľubovoľný smer, z rovníc sme dostali, že má smer dotyčnice k hadici, a teda je to obyčajná ťahová sila. To ale dáva zmysel. Keďže voda pôsobí na hadicu v každom mieste rovnako veľkou silou, nie je ani najmenší dôvod, aby v hadici vznikali dodatočné strižné napätia v dôsledku prúdenia vody v jej vnútri.

---

1. Samozrejme aj zložky v smere osi uhla \(\Delta\phi\) musia byť v rovnováhe. Tie sú však, ako vieme, kompenzované silou \(\Delta F = f\Delta\phi\) od kvapaliny v hadici, preto rovnováhu síl v tomto smere skúmať nemusíme.↩

2. Doplňujúci materiál nad rámec úlohy. Čítať na vlastné riziko.↩

3. analýza pre štvrťkružnicu↩

4. t. j. ten, ktorý je bližšie ku kladnej \(x\)-ovej polosi↩

5. Zákon akcie a reakcie. \(T^{-}\left(\phi\right)\) je sila, ktorou pôsobí predchádzajúci kúsok hadice na nasledujúci v mieste \(\phi\), \(T^{+}\left(\phi\right)\) je sila, ktorou pôsobí nasledujúci kúsok hadice na predchádzajúci v rovnakom mieste.↩

6. Všetky sily sčítavame, lebo v súlade s našou konvenciou sú sily, ktoré majú smer doľava, záporné.↩