6. Fyzik vo fitku II vzorové riešenie

Uvažujme bežiaci pás naklonený pod uhlom \(\alpha\), s povrchom pohybujúcim sa rýchlosťou \(u\) smerom nahor. Súradnicovú sústavu si zvolíme tak, že \(x\)-ová os korešponduje s povrchom pásu a \(y\)-ová os je pochopiteľne na ňu kolmá, pričom leží vo vertikálnej rovine. Poučení úlohou z predchádzajúceho kola si odpustíme obšírne obkecávanie a pustíme sa rovno do riešenia.

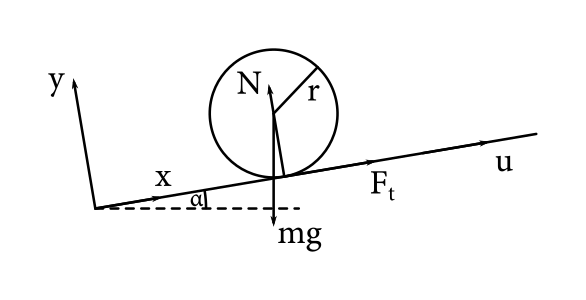
Začnime translačným pohybom. Podľa druhého Newtonovho zákona možno pre \(x\)-ový smer písať \[ ma = F_{t} - mg\sin\alpha. \]

Odtiaľ \[ a = \frac{F_{t}}{m} - g\sin\alpha. \]

V \(y\)-ovom smere k žiadnemu pohybu nedochádza, preto \[ N = mg\cos\alpha. \]

Pre rotačný pohyb písaný vzhľadom na ťažisko platí \[ J\epsilon = F_t r, \] kde \(J = \frac{1}{2}mr^{2}\), teda uhlové zrýchlenie valca je \[ \epsilon = \frac{2F_{t}}{mr}. \]

V prvých momentoch po položení valca na rozbehnutý bežiaci pás valec na ňom prešmykuje. Pre treciu silu vtedy platí \[ F_{t} = fN = fmg\cos\alpha. \]

Po dosadení do výrazov pre zrýchlenia dostávame \[ \begin{aligned} a &= fg\cos\alpha - g\sin\alpha \\ \text{a }\epsilon &= \frac{2fg\cos\alpha}{r}. \end{aligned} \]

Vidíme, že smer pohybu valca závisí od sklonu pásu. Ak je sklon pásu mierny, valec sa rozbehne v smere pôsobenia trecej sily, teda v smere pohybu pásu; ak je sklon strmší, rozbehne sa opačným smerom. Pre sklon \(\alpha = \arctan f\) zostane valec na mieste. Pozor, ale len do momentu, kým nedosiahne dostatočnú uhlovú rýchlosť, pri ktorej prešmykovanie ustane! Následne sa trenie zmení na statické, pre ktoré platí \(F_{t}\leq fmg\cos\alpha\) a valec sa zrejme rozpohybuje. Ale nepredbiehajme! Nájdime najskôr rýchlosť, pri ktorej prešmykovanie ustane.

Translačné aj uhlové zrýchlenie valca sú počas prešmykovania konštantné. To znamená, že v tejto fáze pohybu rastú jeho rýchlosť a uhlová rýchlosť lineárne s časom \[ \begin{aligned} v\left(t\right) &= g\left(f\cos\alpha - \sin\alpha\right)t, \\ \omega\left(t\right) &= \frac{2fg\cos\alpha}{r}t. \end{aligned} \]

Označme si rýchlosť valca v momente zastavenia prešmykovania \(V\) a jeho uhlovú rýchlosť v tomtiež momente \(\Omega\). Prešmykovanie ustane, keď sa rýchlosť bodu na povrchu valca v kontakte s pásom vyrovná rýchlosti pásu \[ u = V + \Omega r. \]

Po dosadení príslušných výrazov za rýchlosti vieme vyjadriť čas, v ktorom prešmykovanie ustane \[ \tau = \frac{u}{g\left(3f\cos\alpha - \sin\alpha\right)}, \] ako aj translačnú a uhlovú rýchlosť v tomto čase \[ \begin{aligned} V &= \frac{f\cos\alpha - \sin\alpha}{3f\cos\alpha - \sin\alpha}u, \\ \Omega &= \frac{2f\cos\alpha}{3f\cos\alpha - \sin\alpha}\frac{u}{r}. \end{aligned} \]

Čo sa bude diať ďalej? Akonáhle prešmykovanie ustane, zrýchlenia valca sa vo všeobecnosti zmenia, pretože statická trecia sila sa vo všeobecnosti líši od dynamickej. Vráťme sa teda k výrazom pre zrýchlenia valca so všeobecnou trecou silou. Pre závislosti rýchlosti a uhlovej rýchlosti valca na čase platí¹ \[ \begin{aligned} v\left(t\right) &= V + \left(\frac{F_{t}}{m} - g\sin\alpha\right)t\\ \text{a }\omega\left(t\right) &= \Omega + \frac{2F_{t}}{mr}t. \end{aligned} \]

Keďže nemá dochádzať k prešmykovaniu, v každom momente musí platiť \[ u = v\left(t\right) + \omega\left(t\right)r. \] Teraz to už chce len trochu obratnosti s úpravou výrazov a nepomýliť sa. Po dosadení za \(v\left(t\right)\) a \(\omega\left(t\right)\) možno nájsť neznámu treciu silu \[ F_{t} = \frac{1}{3}mg\sin\alpha \] a po jej dosadení späť do týchto výrazov konečne dostaneme hľadané závislosti \[ \begin{aligned} v\left(t\right) &= \frac{f\cos\alpha - \sin\alpha}{3f\cos\alpha - \sin\alpha}u - \frac{2}{3}g\sin\alpha t, \\ \omega\left(t\right) &= \frac{2f\cos\alpha}{3f\cos\alpha - \sin\alpha}\frac{u}{r} + \frac{2g\sin\alpha}{3r}t. \end{aligned} \]

Prizrime sa lepšie týmto funkciám. Zrýchlenie translačného pohybu je vždy záporné. To znamená, že valec sa začne valiť nadol po bežiacom páse bez ohľadu na jeho sklon² či súčiniteľ trenia. Kladné uhlové zrýchlenie zase hovorí, že rotácia valca sa bude počas toho zväčšovať, čo dáva perfektný zmysel, ak požadujeme, aby valec neprešmykoval.

Čo ale potom s tou statickou polohou valca, na ktorú sa pýta zadanie? Translačné zrýchlenie valca je \(a = \frac{2}{3}g\sin\alpha\). \(\frac{2}{3} \neq 0\), \(g \neq 0\), takže pokiaľ je aj sklon nenulový a pás sa pohybuje rovnomernou rýchlosťou, nie je možné, aby valec zostal stáť na mieste.

Ak by sme chceli, aby valec stál na mieste, musela by existovať sila, ktorá by pôsobila proti zložke tiažovej sily rovnobežnej s pásom. Počas prešmykovania to bola trecia sila, lenže tá sa po ustatí prešmykovania zmenšila a už nebola schopná vyrovnať tiažovú silu.

Jedinou možnosťou, ako valec udržať na mieste, je teda, že trecia sila neklesne až tak veľmi. To sa dá docieliť tým, že pás bude zrýchľovať. Túto situáciu sme analyzovali už v predchádzajúcom kole.

Ak je zrýchlenie pásu dostatočne veľké – až tak, že valec bude na páse prešmykovať, potom je to ekvivalentné situácii, keď položíme valec na už rozbehnutý bežiaci pás. Vtedy ale vieme, že statická poloha existuje aspoň pre sklon \[ \alpha = \arctan f. \]

Na mieste je otázka, či vieme dosiahnuť statickú polohu aj pre iný sklon. Uvažujme, že pás zrýchľuje, no dostatočne pomaly, takže k prešmykovaniu nedochádza. Potom ale platí presne rovnaký výpočet, ako sme robili pre druhú fázu pohybu, s tým, že \(V = 0\), \(\Omega = 0\) a \(u = u\left(t\right) = a_{p}t\), kde \(a_{p}\) je zrýchlenie pásu. Potom presne rovnakým postupom dostaneme \[ \begin{aligned} F_{t} &= \frac{1}{3}m\left(a_{p} + g\sin\alpha\right) \\ \text{a } v\left(t\right) &= \left(\frac{a_{p}}{3} - \frac{2}{3}g\sin\alpha\right)t. \end{aligned} \]

Odtiaľ z podmienky nulovej rýchlosti valca \[ a_{p} = 2g\sin\alpha. \]

Statickú polohu valca teda možno dosiahnuť aj pre iný sklon, ak bude pás zrýchľovať s takýmto zrýchlením.

Ale pozor, nie pre ľubovoľný sklon, aj keď nám sklon vo výsledku explicitne nevystupuje! Nezabúdajme, že zrýchlenie pásu nemôže byť ľubovoľne veľké, inak valec začne prešmykovať a dostaneme predchádzajúci prípad. Podmienka neprešmykovania je daná maximálnou trecou silou medzi valcom a pásom \[ F_{t} \leq fmg\cos\alpha. \]

Pre maximálne zrýchlenie pásu teda musí platiť \[ \frac{1}{3}m\left(a_{p\ \mathrm{max}} + g\sin\alpha\right) = fmg\cos\alpha, \] odkiaľ \[ a_{p\ \mathrm{max}} = 3fg\cos\alpha - g\sin\alpha. \]

No a napokon z podmienky \(a_{p}\leq a_{p\ \mathrm{max}}\) dostávame, že stacionárnu polohu je možné takýmto spôsobom dosiahnuť, len ak pre sklon pásu platí \[ \tan\alpha\leq f. \]