2. Le-glass vzorové riešenie

Zadanie

Lego sa nedávno hral s ideálnym akváriom tvaru kvádra naplneným vodou. Nejakou náhodou sa mu však na jeho stene podarilo spraviť dieru s výškou \(2r\) a šírkou \(l\). Našťastie mal po ruke sadu homogénnych geometrických telies. Zobral preto valec vhodných rozmerov a pokúsil sa ním dieru upchať.

Majme homogénny valec s hmotnosťou \(m\), výškou \(l\) a polomerom \(r\). Vložme ho do obdĺžnikovej diery v stene akvária (s výškou \(2r\) a šírkou \(l\)) a upevnime ho tak, že sa môže voľne otáčať okolo svojej (horizontálnej) osi. Na začiatku nech je všetko v pokoji. Uvažujte, že voda po obvode diery z akvária nevyteká. Určte uhlové zrýchlenie rotácie valca, pričom úlohu riešte z energetického aj silového pohľadu.

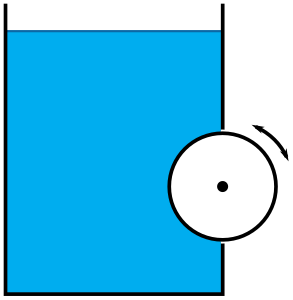
Na to, aby sa valec točil, museli by naň pôsobiť nejaké sily. V situácii, v ktorej sme, sú najrelevantnejšie sily hydrostatického tlaku, ktoré pôsobia kolmo na povrch Legovho valca. Kolmo však znamená, že všetky sily pôsobiace na zaoblenú časť smerujú do osi otáčania valca, čiže nemajú otáčavý účinok, a tie, ktoré pôsobia na podstavy valca, sa navzájom vyrušia. To, že vyššie sú tie sily slabšie a nižšie silnejšie, nám však nič nemení na tom, že ich smer je vždy do osi otáčania.

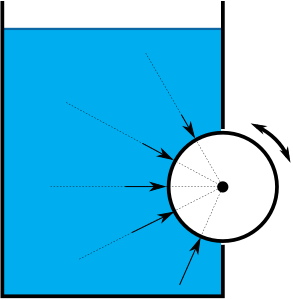
Čo sa týka energie, zo zákona zachovania energie v rámci tejto sústavy vieme, že na to, aby valček konal prácu otáčavým pohybom, musí byť premenená nejaká iná energia tej istej sústavy. Túto zmenu by mohla mať na svedomí jedine voda a následne by sme počítali so vzťahom pre energiu otáčavého pohybu \(E = \frac{1}{2} \frac{I}{\omega^2}\). Voda však svoju energiu nemení – ani neprúdi, ani nevyteká, teda jej energiu valček nevyužíva. Valec sa teda otáčať nebude.