2. Klenoty v Rio Pecos vzorové riešenie

Zadanie

Na dne čírej rieky Pecos v hĺbke \(H = \SI{100}{\metre}\) sa nachádza poklad. Po hladine sa plaví slávny hľadač pokladov Kubo, ktorý vie, že sa v rieke poklad nachádza. Preto sa z malej výšky nad hladinou pozerá do vody. Z akej najväčšej horizontálnej vzdialenosti \(L\) uvidí Kubo poklad na dne rieky? Index lomu vody je \(n = \num{1.331}\) a index lomu vzduchu \(n' = 1\).

Prvou myšlienkou, ktorá nám napadne po prečítaní si zadania úlohy, môže byť napríklad: „Počkať, čo? Však predsa nekonečná, nie?“ Ak je rieka dokonale číra, tak by skrz vodu malo byť vidno aj v nekonečnej vzdialenosti, nie? Táto myšlienka však v našej situácií správna nie je. Správnou by bola v prípade, ak by sa hľadač pokladov Kubo pozeral na poklad spod vodnej hladiny.

Práve vodná hladina je v tejto úlohe bodom zlomu – a to doslova. Na poklad dopadá (i keď cez vodu, ale predsa) slnečné svetlo, ktoré sa od pokladu odráža do všetkých smerov. Tieto lúče smerujú k vodnej hladine, kde sa buď odrazia naspäť alebo prejdú hladinou a v procese sa zlomia – zmenia smer, respektíve uhol voči hladine.

A tu už sa dostávame aj k nejakému fyzikálnemu zákonu. Nech svetelný lúč dopadá na rozhranie dvoch prostredí (v našom prípade vodnú hladinu) pod uhlom \(\theta_1\) voči kolmici na rozhranie a prechádza rozhraním. Potom sa podľa Snellovho zákona zlomí a opúšťa rozhranie pod uhlom \(\theta_2\) voči kolmici na rozhranie, pričom platí \[ \frac{\sin{\theta_1}}{\sin{\theta_2}} = \frac{n_2}{n_1}, \] kde \(n_1\) je index lomu prvého prostredia a \(n_2\) je index lomu druhého prostredia.

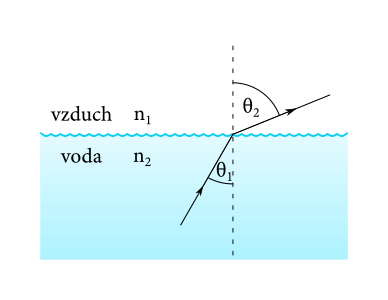
Vidíme však, že táto rovnica, Snellov zákon, veľmi dobre vymedzuje, aký musí byť uhol \(\theta_1\), aby lúč vôbec prešiel rozhraním. Vieme totižto, že uhol \(\theta_2\) musí byť menší ako \(\ang{90}\), inak lúč rozhraním neprechádza, ale odráža sa nazad do vody.

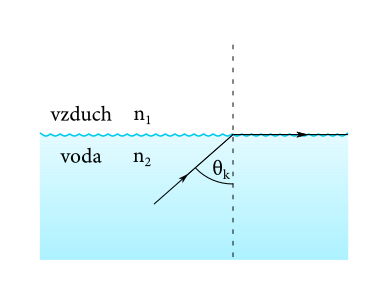
Aby teda lúč vôbec vyšiel z vody (a tak mohol byť uvidený nad hladinou hľadiacim Kubom), musí platiť \(\theta_1<\theta_{k}\), kde \(\theta_k\) je tzv. kritický uhol, teda taký uhol \(\theta_1\), pre ktorý by platilo \(\theta_2 = \ang{90}\). Tento uhol je v našom prípade rovný \[ \theta_k = \arcsin{\left(\frac{n_2}{n_1}\sin{\ang{90}}\right)} = \arcsin{\frac{n_2}{n_1}} = \arcsin{\frac{1}{\num{1.331}} = \ang{48.704}}. \]

Nastať teda môžu tri prípady. Ak bude \(\theta_1>\theta_k\), lúč vychádzajúci od pokladu sa odrazí od hladiny nazad do vody, a teda sa ku Kubovi nedostane. Ak bude \(\theta_1 = \theta_k\), lúč sa šíri rovnobežne s hladinou. Kubo má oči v nejakej výške nad hladinou, avšak veľmi malej. V hraničnom prípade (kedy oko považujeme za bod práve na hladine) teda takýto lúč uvidí. No a samozrejme pre \(\theta_1 < \theta_k\) Kubo lúč uvidí.

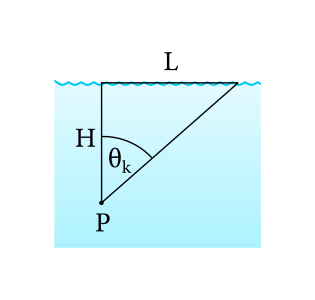
Teraz už ľahko vidíme z obrázka, že pre maximálnu horizontálnu vzdialenosť \(L\), v ktorej Kubo poklad uvidí, musí platiť \[ \tan{\theta_k} = \frac{L}{H}, \] takže \[ L = H\tan{\theta_k} \approx \SI{113.845}{\meter}, \] čo je najväčšia horizontálna vzdialenosť, v ktorej Kubo poklad uvidí.