Zadanie
Krtko v KSP miestnosti vyhrabal čiernu skrinku. Nadšený ju premiestnil do FKS miestnosti a začal ju skúmať. Zo skrinky trčali tri káble. Keď pripojil na prvý a druhý kábel zdroj napätia s hodnotou \(\num{20}\) voltov, voltmeter medzi druhým a tretím káblom mu ukázal \(\num{8}\) voltov. Keď pripojil zdroj napätia na druhý a tretí kábel, voltmeter medzi prvým a tretím káblom ukázal \(\num{15}\) voltov. Nájdite čo najviac rôznych schém vnútra skrinky, ak viete, že obsahuje iba rezistory. Za rôzne schémy sa považujú tie, ktoré sa na seba nedajú transformovať nahradením jedného rezistora niekoľkými sériovo alebo paralelne zapojenými rezistormi. Body Vám budu udelené podľa toho, koľko schém nájdete, pričom ten kto ich z Vás nájde najviac bude mať určite \(\SI{9}{b}\).
Začneme tým, že sa chceme ospravedlniť za pôvodné zadanie. Nájsť všetky možné zapojenia nie je také jednoduché, ako sme si mysleli.
A teraz k tým podstatným veciam. Najjednoduchšie zapojenie bude vyzerať určite tak, že spojíme každý bod s každým práve jedným vodičom s rezistorom. To znamená, že v čiernej skrinke nebude žiaden uzol naviac. Otázkou teraz zostáva, či z takéhoto zapojenia vieme vyrobiť jednoducho iné zapojenie, ktoré by malo iný počet uzlov, inak povedané také, ktoré by podľa zadania nebolo rovnaké. (Rozdelenie rezistora na dva sériovo alebo paralelne zapojené rezistory nemení počet uzlov.) Ukazuje sa, že vieme, a to vďaka zapojeniu trojuholník-hviezda1 To znamená, že týmto spôsobom si vieme zadarmo vyrobiť zapojenie, ktoré má rovnaký počet odporov, ale o uzol viac. Počet odporov zas vieme meniť nahradením jedného odporu za dva paralelné. Už vidíte kam tým smerujeme? Stačí vziať najjednoduchšie zapojenie v tvare trojuholníka, odpor na každej strane nahradiť veľa paralelnými a dostaneme tak veľa trojuholníkov pospájaných vo vrcholoch. A teraz môžeme na každý z nich aplikovať transformáciu trojuholník-hviezda, čím dostaneme zapojenia s rôznym počtom vrcholov. Poradie týchto ekvivalentných operácií môžeme dokonca medzi sebou prestriedať, no tak či onak, teoreticky je takýchto rôznych zapojení nekonečno.
[@P]{postup}{pdf}{png}{30mm}{}{}
Ešte nám však zostáva dokázať, že aspoň jedno z takýchto ekvivalentných zapojení bude môcť spĺňať hodnoty uvedené v zadaní. Keďže sme leniví (a múdri, pekní, skromní), ukážeme to na výpočtovo najjednoduchšom zapojení, hviezde s troma rezistormi ako na obrázku.
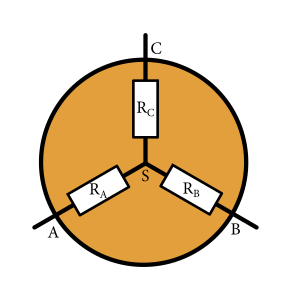
Podľa zadania, keď zapojíme \(\SI{20}{\volt}\) zdroj na uzly A a B, tak medzi uzlami B a C nameriame napätie \(\SI{8}{\volt}\). Cez odpor \(R_{\rm C}\) prúd netečie a medzi uzlami A a B je prúd nemenný. Ohmov zákon hovorí, že napätie sa v sériovo zapojených rezistoroch rozloží priamo úmerne odporu rezistorov. Pomer odporu \(R_{\rm B}\) k odporu celej vetvy, cez ktorú preteká prúd teda je \[ \frac{R_{\rm B}}{R_{\rm A} + R_{\rm B}} = \frac{U'_{\rm SB}}{U'_{\rm AS} + U'_{\rm SB}} = \frac{8}{20}. \] Podobne, ak zapojíme zdroj medzi uzly B a C, cez odpor \(R_{\rm A}\) prúd nepotečie a na odpore \(R_{\rm C}\) nameriame spád napätia \(\SI{20}{\volt}\). Pre pomer odporov teda platí \[ \frac{R_{\rm C}}{R_{\rm B} + R_{\rm C}} = \frac{U''_{\rm SC}}{U''_{\rm BS} + U''_{\rm SC}} = \frac{15}{20}. \] Máme dve lineárne rovnice o troch neznámych, ktoré hravo vyriešime. Vyjde nám \(R_{\rm A} = \frac{3}{2} R_{\rm B}\) a \(R_{\rm C} = 3 R_{\rm B}\) s vôľou v odpore \(R_{\rm B}\), čo nie je prekvapením na počet nezávislých rovníc.
No a to je všetko. Ukázali sme na pár riadkoch, že vieme nájsť nekonečne veľa riešení problému a pre to najjednoduchšie zapojenie sme ho aj našli. Na šestku celkom ľahké, nie?
Ako presne spraviť túto transformáciu nebudeme vysvetlovať, no ak to neviete, nájdete to napríklad na wikipédii https://en.wikipedia.org/wiki/Y-Δ_transform.↩︎
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.