7. Ríša nezapadajúceho slnka vzorové riešenie

Rovno sa priznám, že táto úloha bola riadny chyták. Dala sa totiž rýchlo a nesprávne vyriešiť iba s použitím zákona zachovania energie. Teda spočítať, koľko energie dopadá na zrkadlo zo Slnka, preškálovať na veľkosť mesta a potom už len dorátať, aké zakrivenie treba na to, aby sa lúče koncentrovali práve na zemskom povrchu.

Takto jednoducho to ale vôbec nefunguje: svetlo sa zrkadlami a šošovkami nedá koncentrovať ľubovoľne. Dalo by sa to spraviť iba v prípade, ak by Slnko bolo bodovým zdrojom svetla. V tejto úlohe však takúto aproximáciu nemôžeme použiť. Lúče zo Slnka nie sú dokonale rovnobežné a teda nie je možné ich parabolickým zrkadlom sústrediť do ľubovoľne malého bodu.¹

Prečo? Musíme si uvedomiť, čo vlastne také zrkadlo robí. Napriek rozšírenému presvedčeniu ani parabolické zrkadlo nedokáže lúče zosilniť. V ponímaní klasickej fyziky je dráha každého lúča priamka, zrkadlo ju akurát môže zalomiť podľa zákona odrazu, ale nič viac – intenzita² sa musí zachovávať. Jediné, čo sa môže zmeniť, je smer.

Parabolické zrkadlo akurát dokáže zariadiť, aby v ohnisku bolo viac smerov, z ktorých prichádza svetlo; konvexné zrkadlo naopak obraz Slnka zmenší a smerov je menej. Ak by sme urobili fotku digitálnym fotoaparátom, každý osvetlený pixel bude presne rovnako jasný, ako keby sme odfotili priamo Slnko. Vo vesmíre, kde je iba Slnko a nejaké zrkadlá, v každom bode oblohy vidíme buď tmu (nulová intenzita žiarenia) alebo Slnko (nejaká konštantná intenzita, označme ju \(I_\odot\)). Pre optimálne zrkadlo je zrejmé, že v každom jeho bode vidíme Slnko – teda lúč vychádzajúci z nášho oka po odraze od zrkadla pretne povrch Slnka.

No a to je vlastne všetko. Ostáva nám určiť, koľko svetla potrebujeme, aby nás zrkadlo osvetlilo rovnako, ako Mesiac v splne. To sa dá spočítať, môžeme si ale pomôcť nejakými zdrojmi, hoci Wikipediou. V astronómii sa na meranie zdanlivých jasností objektov používa magnitúdová škála. Tá nie je lineárna, ale logaritmická, podobne ako napríklad decibely, ktoré poznáme z akustiky.

Rozsah jasností nebeských objektov je totiž obrovský: Slnko je asi \(10^{13}\)-krát jasnejšie, než najslabšia hviezda, ktorú vidíme voľným okom, alebo \(10^{26}\)-krát jasnejšie než najslabšia hviezda, ktorú zachytí Hubblov ďalekohľad. Na rozdiel od decibelu má ale táto škála z historických dôvodov nešťastne zvolený základ: rozdiel piatich magnitúd zodpovedá stonásobnému rozdielu v jasnosti. Rozdiel jednej magnitúdy teda zodpovedá rozdielu jasností \(100^{1/5} = 10^{\num{0.4}} \doteq \num{2.512}\), a navyše je škála obrátená, teda menšia magnitúda zodpovedá jasnejšiemu objektu.

Keď si nájdeme údaje pre Mesiac a Slnko, zistíme, že \(m_\odot = \num{-26.7}\) a \(m_\text{\Moon} = \num{-12.7}\). Rozdielu štrnástich magnitúd zodpovedá pomer jasností \(100^{14/5} \approx 400000\). Slnko je teda približne štyristotisíckrát jasnejšie, ako Mesiac v splne. Keďže intenzita sa zachováva, potrebujeme, aby sme zrkadlo videli 400000-krát menšie, než je uhlový rozmer Slnka. Mohli by sme to spočítať ako plošný uhol v steradiánoch; môžeme ho však preškálovať jednoduchou priamou úmerou a dostaneme, že pre okrúhle zrkadlo \[ \frac{S}{\left(\SI{35786}{\kilo\metre}\right)^2} = \frac{\frac{\pi R_\odot^2}{\left(\SI{1}{AU}\right)^2}}{400000} \qquad\Rightarrow\qquad S \doteq \SI{218000}{\metre\squared}, \] kde \(\SI{35786}{\kilo\metre}\) je výška geostacionárnej orbity nad povrchom. Dobre teda poslúži akékoľvek zrkadlo s prierezom v smere kolmice aspoň \(\SI{218000}{\metre\squared}\) a takým polomerom krivosti, aby sme pri pohľade z mesta v každom jeho bode videli časť slnečného disku. Najmenšiu možnú plochu určite bude mať ploché zrkadlo, musíme však overiť, či v plochom zrkadle s takýmto uhlovým rozmerom môžeme vidieť celé Slnko. Nemusíme však vôbec nič počítať: pre ploché zrkadlo platí, že ak je jeho uhlový rozmer menší, ako rozmer pozorovaného objektu, objekt v ňom môžeme vidieť celý.³

Z praktických dôvodov bude najlepším tvarom kruh, pričom správnej ploche zodpovedá polomer \(\SI{263}{\metre}\).

Veľkosť mesta

Iste ste si všimli, že v riešení veľkosť mesta nikde nevystupuje a teda na nej nezáleží. Nie je to úplne pravda, pretože mesto nemôže byť ľubovoľne veľké. Existuje však horné ohraničenie, čiže najväčšia veľkosť plochy na povrchu Zeme, na ktorej bude každý bod osvetlený celým zrkadlom – čiže veľkosť „prasiatka“. Okolo neho bude ešte prstenec ožiarený iba časťou zrkadla, a nakoniec tma.

Koľko to bude? Miesto zrkadla na opačnej strane oblohy, ako je Slnko, si predstavme štrbinu s rovnakými rozmermi a v rovnakej vzdialenosti, ale medzi nami a Slnkom. Nakreslime si to.

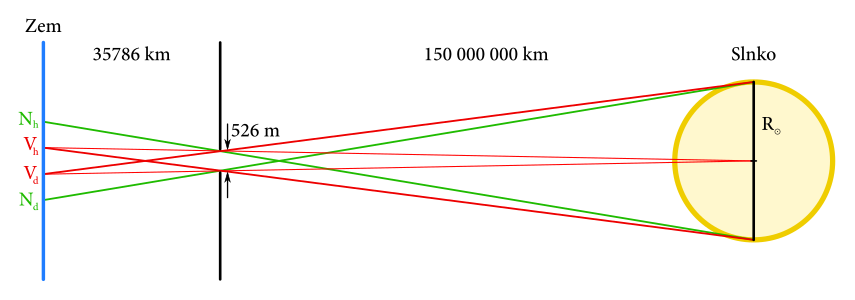
Toto už je jednoduchá geometria s priamkami. V kartézskej sústave dokážeme určiť ich sklon a vyjde nám, že so Zemou sa pretínajú \(\SI{167}{\kilo\metre}\) od osi, takže priemer prasiatka musí byť \(\SI{334}{\kilo\metre}\) a mesto musí byť menšie. S tým snáď zatiaľ nemajú problém ani v Číne.

Ďalšie dôvody, prečo malé parabolické zrkadlo nestačí

Na záver skúsme analyzovať zjavné, ale nesprávne riešenie, teda pozorovateľa v ohnisku malého parabolického zrkadla. Intuitívne by sa nám toto mohlo javiť ako najlepšie.

V skutočnosti toto riešenie nie je úplne zlé, nesmieme ale zabudnúť na podmienku rovnobežnosti lúčov. Predstavme si všetky lúče odrazené od zrkadla, ktoré dopadajú do jeho oka. Tvoria kužeľ s vrcholom v oku. Keďže zrkadlo je parabolické, pred odrazom od jeho povrchu museli byť tieto lúče rovnobežné. Pozorovateľ teda v zrkadle nevidí celé Slnko, ale iba malú časť jeho povrchu – rovnako veľkú, ako je samotné zrkadlo. A aj z tejto plochy do jeho oka smeruje iba maličká časť lúčov, úmerná uhlovému rozmeru zrkadla pri pohľade zo Slnka. Lúče, ktoré nie sú rovnobežné s osou zrkadla, po odraze skončia inde, než v pozorovateľovom oku. Po poctivom spočítaní nám vyjde opäť rovnaká plocha prierezu, ako pri plochom zrkadle.

Naopak vo vypuklom zrkadle so správnym polomerom krivosti by sme dokázali vidieť akurát celú plochu Slnka, po odraze by sa však lúče rozptýlili do väčšieho plošného uhla. Zdanlivá jasnosť by potom bola opäť rovnaká.

Iným dobrým argumentom je prvý termodynamický zákon. Ak by sa svetlo dalo zrkadlom koncentrovať do ľubovoľne malej plôšky, celkový svetelný tok by mohol byť väčší, ako na povrchu Slnka. Zo Stefan–Boltzmannovho zákona potom ale plynie, že rovnovážna teplota v tomto bode by bola vyššia, ako teplota Slnka. Potom by sme mohli zostrojiť hypotetický tepelný stroj, ktorý by túto plôšku používal ako zdroj tepla a Slnko ako chladič. Tým by sa Slnko ďalej zohrievalo, a teda by sme mali perpetuum mobile, čo však určite nejde.