1. Cestný pirát vzorové riešenie

Uvažujme auto, ktoré sa pohybuje rovnomerne priamočiaro rýchlosťou \(v\). Začneme tým, že sa zamyslíme, prečo vlastne takéto auto potrebuje nejaké palivo. Veď predsa, ak sa pohybuje rovnomerne, tak podľa zákona zotrvačnosti by malo v tomto pohybe zotrvávať aj bez toho, aby muselo nejaké palivo spaľovať.

Pozrime sa na to, prečo pri pohybe auta dochádza k stratám jeho energie. Jednak musí auto prekonávať vonkajšie odporové sily, ako sú odpor vzduchu či valivé trenie. No a potom sú tu vnútorné straty napríklad v dôsledku trenia medzi jednotlivými komponentami auta. A práve na kompenzáciu týchto strát je potrebné neustále dodávanie energie.

V prvom rade si musíme určiť, ktoré straty sú tie relevantné. Odhadnime si teda najskôr veľkosti jednotlivých síl.

Začnime valivým trením. Tu nebudeme musieť veľa počítať, aby sme ho vedeli kvantifikovať. Pre valivé trenie totiž platí, že sila valivého trenia je daná vzťahom \(F_{r} = \xi\frac{N}{r}\), kde \(\xi\) je rameno valivého odporu dané mierou deformácie, \(N\) je normálová sila o podložku a \(r\) je polomer kolesa. V západných krajinách sa častejšie uvádza tento vzťah v podobe \(F_{r}=C_{r}N\), kde \(C_{r}=\frac{\xi}{r}\) je súčiniteľ valivého odporu. Pre naše auto platí \(F_{r}=C_{r}Mg\). ¹ Súčiniteľ valivého odporu závisí od miery nafúkania kolesa, hrúbky dezénu, tvrdosti pneumatiky, typu povrchu, po ktorom auto jazdí, a mnohých ďalších faktorov. Pre bežnú pneumatiku na asfalte je \(C_{r}\sim\num{0.01}\). Hmotnosť auta je \(M\sim\SI{1}{\tonne}\). Dostávame teda \(F_{r}\sim\SI{100}{\newton}\).

Poďme teraz na odpor vzduchu. Ten je daný Newtonovým odporovým vzťahom \(F_{a}=\frac{1}{2}C_{a}S\rho_{a}v^{2}\), kde \(C_{a}\) je koeficient odporu zohľadňujúci tvar auta, ktorý však nie je konštantný, ale závisí od rýchlosti², \(S\) je čelná plocha a \(\rho_{a}\) je hustota vzduchu. Pre auto \(C_{a}\sim\num{0.4}\), \(S\sim\SI{2}{\metre\squared}\) a \(\rho_{a}\sim\SI{1.3}{\kilo\gram\per\metre\cubed}\). To dáva \[ F_{a} \sim \SI{0.4}{\kilo\gram\per\metre} \cdot v^{2} \sim \begin{cases} \SI{77}{\newton}\text{,} & v=\SI{50}{\kilo\metre\per\hour},\\ \SI{250}{\newton}\text{,} & v=\SI{90}{\kilo\metre\per\hour},\\ \SI{522}{\newton}\text{,} & v=\SI{130}{\kilo\metre\per\hour}. \end{cases} \]

Vidíme, že príspevky oboch odporových síl sú v danom rozsahu rýchlostí porovnateľné, pričom pri vyšších rýchlostiach dominuje odpor vzduchu, ktorý rastie kvadraticky s rýchlosťou. Preto treba uvažovať oba zdroje strát. Ešte sme neodhadovali vnútorné straty, no tie zahrnieme do účinnosti spaľovacieho motora neskôr.

Poznajúc zdroje strát energie, môžeme teraz odhadnúť spotrebu paliva, aby sme tieto straty kompenzovali. Spotreba auta sa udáva v litroch na 100 kilometrov. To znamená, že všetko, čo potrebujeme spraviť, je vyčísliť prácu odporových síl na tejto vzdialenosti. Tá je rovná \(W=Fs\), kde \(F\) je celková veľkosť vonkajších odporových síl. Na druhej strane pri spálení benzínu s objemom \(V\) sa uvoľní energia \(E=H\varrho V\), kde \(H\) je výhrevnosť benzínu a \(\varrho\) jeho hustota. Auto nedokáže efektívne využiť všetku túto energiu, ale má nejakú účinnosť \(\eta\). Zrejme platí \(W=\eta E\). Po dosadení za prácu a energiu dostávame rovnosť \(Fs=\eta H\varrho V\).

Označme si spotrebu auta ako \(B\). Ak ju chceme vyčísliť v litroch na sto kilometrov, musíme ju definovať ako \[ B\mathrm{\left[\frac{\si{\litre}}{\SI{100}{\kilo\metre}}\right]}=\frac{1000V}{\num{0.00001}s}=10^{8}\frac{V}{s}. \]

Z energetickej bilancie máme \(\frac{V}{s}=\frac{F}{\eta H\varrho}\), čiže \[ B\mathrm{\left[\frac{\si{\litre}}{\SI{100}{\kilo\metre}}\right]}=10^{8}\frac{F}{\eta H\varrho}. \]

Účinnosť motora je \(\eta\sim\frac{1}{3}\), výhrevnosť benzínu \(H\sim\SI{40}{\mega\joule\per\kilo\gram}\) a jeho hustota \(\varrho\sim\SI{750}{\kilo\gram\per\metre\cubed}\). To dáva \[ B \sim 10^{-2}\frac{\frac{\si{\litre}}{\SI{100}{\kilo\metre}}}{\si{\newton}}\cdot F \sim \begin{cases} \num{1.77}{\frac{\si{\litre}}{\SI{100}{\kilo\metre}}}\text{,} & v=\SI{50}{\kilo\metre\per\hour},\\ \num{3.5}{\frac{\si{\litre}}{\SI{100}{\kilo\metre}}}\text{,} & v=\SI{90}{\kilo\metre\per\hour},\\ \num{6.22}{\frac{\si{\litre}}{\SI{100}{\kilo\metre}}}\text{,} & v=\SI{130}{\kilo\metre\per\hour}. \end{cases} \]

Na záver sa pozrime, či to, čo sme vypočítali, zodpovedá realite. Po chvíľke googlenia sa dopátrame, že v súčasnosti sa priemerná spotreba nových áut pohybuje na úrovni \(\num{8.1}\frac{\si{\litre}}{\SI{100}{\kilo\metre}}\). To je spotreba v bežnej premávke, kde auto nejazdí rovnomerne, ale musí brzdiť, potom zase zrýchľovať, čo stojí energiu. Navyše je to priemer cez všetky autá, takže sú tam zarátané i športové autá, ktoré majú obyčajne vysokú spotrebu, či mohutné terénne autá, ktoré vďaka vyššej hmotnosti a nie práve aerodynamickému tvaru majú tiež vysokú spotrebu.

Ešte nám zostáva zodpovedať na poslednú otázku. Rastie spotreba rýchlo pri vysokých rýchlostiach? Vieme, že príspevok odporu vzduchu k stratám rastie kvadraticky s rýchlosťou, takže pri vysokých rýchlostiach naozaj spotreba rastie rýchlo. Lenže čo to znamená vysoká rýchlosť? Pre spotrebu možno písať vzťah \(B\mathrm{\left[\frac{\si{\litre}}{\SI{100}{\kilo\metre}}\right]}\sim1+\num{0.004}v^{2}\). Potom vysoká rýchlosť v našom ponímaní spĺňa podmienku \(\num{0.004}v^{2}\gtrsim1\), čo znamená \(v\gtrsim\SI{57}{\kilo\metre\per\hour}\).

Dodatok: Motor auta ako cyklista

Keďže mnoho riešiteľov sa začalo zaoberať účinnosťou motora pri daných rýchlostiach, tu je stručné (a možno aj nie) vysvetlenie, ako to s tou účinnosťou naozaj funguje.

Motor v aute funguje ako cyklista na bicykli. Cyklista má obmedzené množstvo sily, ktorou vie tlačiť do pedálov a taktiež obmedzenú rýchlosť, akou vie krútiť nohami. Motor je na tom podobne. Aby sa auto vedelo rozbehnúť a zároveň, aby sa nezadýchalo pri trochu väčšej rýchlosti, auto má prevodovku, ktorá funguje rovnako ako „prehadzovačka“ na bicykli.

Ako bolo vyššie spomenuté, na auto, ale aj na bicykel pôsobia odporové sily, ktoré pôsobia proti smeru jazdy cyklistu, bez ohľadu na ním zvolený prevod. Ak sa ale cyklista hýbe aj konečnou rýchlosťou, tak máme požiadavku nielen na vynaloženú silu, ale aj na vynaloženú „rýchlosť krútenia“ (ak si niekto z vás spravil rozmerovú analýzu, \(Fv = P\), čo je výkon). Takže cyklista má ako vstup výkon, ktorý je od neho vyžadovaný.

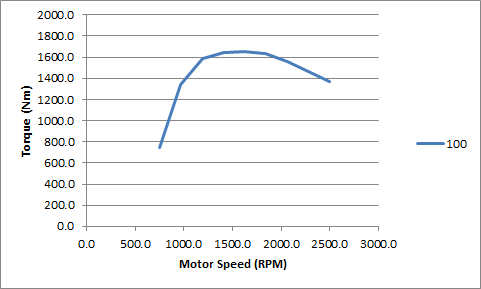
Na ilustračnom obrázku máme „silovú charakteristiku“ motora. Znova sa na to pozrime z pohľadu cyklistu. Os \(y\) uvažujme ako maximálnu silu, ktorú vie cyklista vyvinúť, a os \(x\) ako rýchlosť krútenia jeho nôh. Ak sme už niekedy sedeli na bicykli, je nám dobre známe, že ak veľmi rýchlo krútime nohami, nevieme vynaložiť tak veľkú silu, ako keď sa postavíme do pedálov. V samotnom motore totiž nastávajú explózie stlačeného benzínu a vzduchu, ktoré dajú najviac sily na pohon auta práve pri určitej rýchlosti piestov.

Ďalší obrázok (s tými istými osami ako v minulom obrázku) ukazuje graf účinnosti motora:

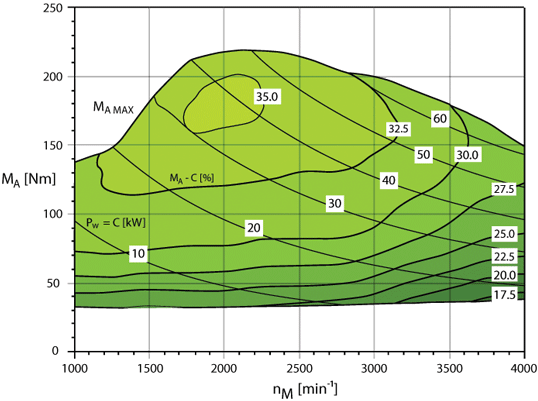
Účinnosť hovorí o pomere, koľko mechanickej energie na pohyb auta dopredu dostaneme z pôvodnej celkovej tepelnej energie (výhrevnosti) paliva. V modeli s cyklistom sa to dá predstaviť tak, že koľko energie minieme na pohon bicykla, a koľko len na samotný pohyb nôh. Ako si môžme všimnúť, v prvej časti vzoráku sme uvažovali účinnosť motora 30%, čo podľa grafu približne (pre odhad) dáva zmysel. Ak ste sa však rozhodli špekulovať nad otáčkami motora/rýchlosťou krútenia nôh, poďme si rozobrať, čo na obrázku vidíme. Šikmé čiary s označeniami \(\num{10}-\num{60}\left(\si{\kilo\watt}\right)\) ukazujú požadovaný výkon od cyklistu (alebo motora), a vrstevnice a farby odlišujú jednotlivé účinnosti. Prečo sú šikmé čiary šikmé? Pri analógii s bicyklom to dáva zmysel: čím ľahší prevod zvolíme, tým ľahšie sa nám šľape do pedálov, ale tým rýchlejšie musíme krútiť nohami. Nič nie je zadarmo. Prečo je ten graf hore taký vlnitý? Horné ohraničenie je presne ako prvý obrázok.

Taktiež môžme vidieť, že daný motor by už nebol schopný dodať výkon \(\SI{70}{\kilo\watt}\) (tj. má „maximálny výkon“ okolo \(\SI{65}{\kilo\watt}\).) Čo je na tomto grafe najzaujímavejšie je, kde je motor najefektívnejší. Hoci by človek pri aute intuitívne povedal, že s najťažším prevodom a najnižšími otáčkami je spotreba najmenšia, nemusí to byť pravda. Pre veľmi malé výkony \(\SI{10}{\kilo\watt}\) sa to podľa grafu tak zdá (sme v najžltšej vrstevnici) – zvolíme najťažší prevod, máme najmenšie otáčky, účinnosť je najväčšia.

Avšak ak sa pozrieme na čiary \(\frac{\SI{30}{\kilo\watt}}{\SI{40}{\kilo\watt}}\), je zrejmé, že niekedy sa oplatí použiť nižší prevodový stupeň, aby sme dosiahli lepšiu účinnosť. Pri každom automobile ale závisí od jeho sprevodovania, (nakoľko sa zo spojitých čiar pre výkon stanú diskrétne body – pre každý požadovaný výkon si môžeme vybrať z niekoľkých prevodov, kde každý má danú silu, akou treba pôsobiť a otáčky) a od charakteristiky jeho motora, ktoré sa môžu výrazne líšiť. Ak ideme teda riešiť účinnosť, vždy je potrebné vedieť, aký výkon od auta vyžadujeme – ten sa výrazne mení pri rôznych rýchlostiach: \[ P \sim F v\sim \begin{cases} \SI{1070}{\watt}, & v=\SI{50}{\kilo\metre\per\hour}, \\ \SI{6250}{\watt}, & v=\SI{90}{\kilo\metre\per\hour}, \\ \SI{18850}{\watt}, & v=\SI{130}{\kilo\metre\per\hour}. \end{cases} \]

Každopádne, každé priemerné, rozumne sprevodované auto bude pracovať pri všetkých týchto rýchlostiach niekde v rozmedzí 25-40-percentnej účinnosti, čo nemá veľký vplyv na celkový výsledok spotreby v porovnaní s veľkosťou odporových síl.