Zadanie
Simon sa v poslednom čase začal okrem prechádzania a opravovania starých príkladov venovať aj hudbe. Skúšal gitaru, flautu, trúbku a rôzne iné strunové a dychové hudobné nástroje. Napriek tomu, že nie je špičkový odborník v tejto oblasti, všimol si, že hudobný nástroj znie inak, keď na ňom hrá vonku. Domyslel si, že by to mohla spôsobovať teplota.
Simon by ako správny fyzik rád svoju teóriu experimentálne overil. No kto má čas na to overovať všetky svoje trhlé myšlienky? Možno keby na potvrdenie teórie stačil jeden nástroj, tak dobre, ale čím viac, tým viac. Preto pomôžte Simonovi a zmerajte, ako sa mení frekvencia vášho obľúbeného strunového alebo dychového hudobného nástroja v závislosti od teploty okolia.
Predtým, ako sa bezhlavo pustíme do strkania klavírov, gitár, fláut či huslí do mrazničiek alebo sáun, zamyslime sa, čo by sme mali od merania očakávať. Zadanie nám napovedá, že sa bude nejak meniť tón. Otázkou však ostáva, prečo? No, možností máme hneď niekoľko:
Teplotná rozťažnosť materiálov, z ktorých je náš hudobný nástroj. Obzvlášť citlivé by na to mali byť kovové struny. Vplyvom tepla sa struny predĺžia, čo spôsobí ich uvoľnenie. Struny sa teda natiahnu. Tým pádom sa zvýši vlnová dĺžka a zníži frekvencia.
Zvuk je mechanické vlnenie šíriace sa vzduchom. Rýchlosť, ktorou sa šíri, však nie je konštantná ale závisí od teploty ako \[ c = \num{331,57} + \left(\num{0,607} \cdot T\right)\si{\meter\per\second}. \] To je spôsobené tým, že rýchlosť zvuku je závislá od hustoty vzduchu a obe veličiny, sú závislé od teploty.
Ako vidíme čím vyššia je teplota, tým vyššia je rýchlosť šírenia vĺn. A zároveň vieme, že pre vlny platí vzťah \[ \lambda = \frac{c}{f}. \] Ak teda budeme predpokladať, že vlnová dĺžka sa nemení, potom musí jasne stúpnuť frekvencia.
Došli sme teda ku dvom rôznym záverom – jeden nám hovorí, že frekvencia sa bude znižovať, pretože sa nám uvoľnia struny. Tento jav však bude mať minimálny vplyv na nástroje s malou teplotnou rozťažnosťou, ako je napríklad flauta. Druhý nám naopak hovorí, že frekvencia s teplotou porastie. Tento jav by mal byť pri všetkých nástrojoch zhruba rovnako viditeľný.
Teraz, keď máme nejakú predstavu o tom, čo by sme mohli namerať, môžeme si premyslieť, ako to chceme namerať. Ak chceme rozumne zmerať závislosť, budeme potrebovať aspoň tri, ideálne viac rôznych teplôt, pri ktorých pokus uskutočníme. Ak máte prázdnu mrazničku, tak ako ja, viete sa pohybovať v teplotách od \(\SI{-28}{\celsius}\) až po \(\SI{80}{\celsius}\) pri ohrievaní v rúre. Do vyšších teplôt by som už radšej nešiel. Potom by sa mohla flauta začať topiť a to rozhodne nechceme. Meranie samozrejme netreba zabudnúť zopakovať pre všetky teploty viackrát, pre tento krát bude päť opakovaní stačiť.
Pre dychové nástroje by bolo ideálne fúkať vzduch danej teploty priamo do nástroja, no vzhľadom na niektoré už vcelku extrémne teploty, ktoré by nemusela zniesť batéria, ktorou by sme ventilátor napájali, budeme si musieť vystačiť s vlastným dychom. To samozrejme prináša problémy, pretože vzduch vychádzajúci z našich pľúc určite nebude mať \(\SI{-28}{\celsius}\), či \(\SI{80}{\celsius}\). Kým opustí nástroj, určite zmení svoju teplotu. Naše meranie teda nebude zrovna najpresnejšie, ale dostaneme aspoň rádový odhad, aký vplyv má teplota na dychový hudobný nastroj.
Pre strunové nástroje by to mohlo byť jednoduchšie, netreba do nich fúkať. No, väčšina z nich sa nezmestí do mrazničky alebo rúry a sú omnoho citlivejšie na poškodenie. Taktiež naša teória naznačuje, že jav by pri strunových nástrojoch mal byť menej výrazný.
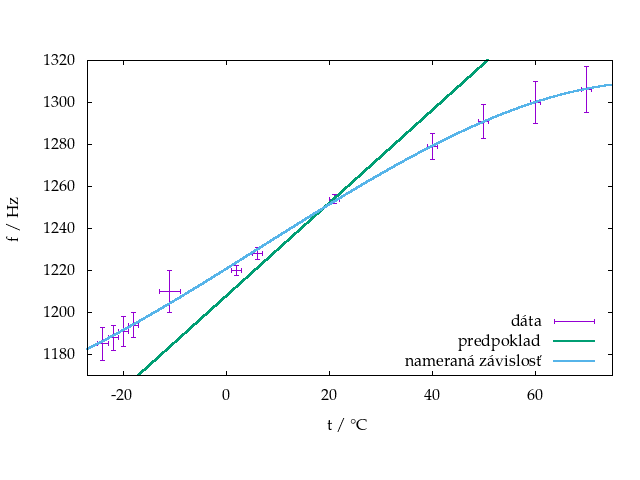
Ako vidíte na grafe, ja som pokus realizoval s flautou. Hodnoty vcelku zodpovedajú naším predpokladom a teda môžeme vidieť, že pri extrémnejších teplotách sme naozaj boli nepresnejší, čo sa dalo očakávať, keďže som do flauty fúkal vzduch zo svojich pľúc.
Na záver by som ešte spomenul, že na analýzu nahrávky ste mohli použiť napríklad Audacity.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.