5. Jarovo súpoistie vzorové riešenie

Kvalitatívny rozbor

Uvažujme súpoistie pozostávajúce z \(2n\) poistiek. Keďže jednotlivé poistky majú nejaký odpor \(R\), celkový odpor \(R_{n}\) súpoistia je nenulový. Akonáhle pripojíme súpoistie k zdroju a napätie začneme pomaly zvyšovať, začne rásť prúd pretekajúci obvodom. Zo začiatku je závislosť prúdu na napätí pekná, lineárna, s konštantou úmernosti \(\frac{1}{R_{n}}\). Nič nenasvedčuje tomu, že by sa to malo niekedy zmeniť. No potom sa to zrazu pokazí. Akonáhle napätie prekročí istú hodnotu, prúd pretekajúci cez nejakú poistku dosiahne jej limit a tá sa prepáli, čím sa efektívne zmení odpor súpoistia.

Zamyslime sa najskôr nad tým, v akom poradí sa budú poistky prepaľovať. To nie je až taký veľký problém zistiť. Stačí, keď si uvedomíme, ako bolo súpoistie skonštruované. Na každej úrovni totiž pozostáva z poistky s odporom \(R\) a o úroveň nižšieho súpoistia, ktoré je sériovo zapojené s ešte jednou poistkou.

Začnime odvnútra. Na prvej úrovni máme len dve paralelné poistky, ktorých výsledný odpor je \(R_{1}=\frac{R}{2}\). Na druhej úrovni sa k nim do série pridá jedna poistka, takže dostaneme zapojenie s odporom \(\frac{3}{2}R\). Tento diel pripojíme paralelne k poistke s odporom \(R\).

A teraz prichádza kľúčová myšlienka. Pri paralelnom zapojení sa prúd rozdelí medzi obe vetvy, takže keď k odporu pripojíme ľubovoľne veľký, ale konečný odpor, výsledný odpor sa zníži a bude menší než odpor ktorejkoľvek z vetiev obvodu. To znamená, že v našom prípade bude výsledný odpor na ľubovoľnej úrovni menší než \(R\). No a keďže vždy máme jednu vetvu pozostávajúcu z práve jednej poistky, jej odpor je \(R\), a druhú vetvu obsahujúcu blok s odporom menším než \(R\) sériovo pripojený k poistke s odporom \(R\), výsledný odpor druhej vetvy bude z intervalu \(\left(R;2R\right)\). To znamená, že väčší prúd bude tiecť vždy cez vetvu s osamotenou poistkou. No a keďže táto sa prepáli už pri prúde \(I\), súpoistie sa začne prepaľovať pekne od vonku.

Teraz si môžeme povedať, ako sa zmení prúd pretekajúci hlavnou vetvou obvodu, keď sa prepáli jedna poistka. Kľúčovou myšlienkou je, že ak je súpoistie dostatočne veľké a prepáli sa vonkajšia poistka, efektívne dostaneme o jedno menšie súpoistie, ktoré má ale takmer rovnaký odpor ako pôvodné, a k nemu je do série predradený ešte jeden dodatočný odpor \(R\). To znamená, že výsledný odpor sa po prepálení poistky zvýši zhruba o \(R\), čo má za následok, že prúd v obvode klesne.

Správanie obvodu bude teda nasledovné. Prúd bude najskôr lineárne rásť s napätím až do momentu, kedy sa prepáli prvá poistka. V tomto okamihu prúd skokovo poklesne. Pri ďalšom zvyšovaní napätia začne prúd opätovne rásť, až dosiahne približne hodnotu pred prepálením poistky a v tomto momente sa prepáli ďalšia poistka. Tento cyklus sa bude opakovať až dovtedy, kým bude počet zostávajúcich poistiek dostatočne veľký.

A čo sa bude diať, keď bude zostávajúce súpoistie malé? Vtedy už prestane platiť, že odpor sa zvýši zhruba o \(R\), pretože zostávajúca časť sa na pôvodnú nebude veľmi podobať a prúd po prepálení poistky porastie na inú hodnotu. Čo znamená malé súpoistie, si povieme o chvíľku.

Poznamenajme ešte, že keď zostanú posledné dve paralelne zapojené poistky, tak každou z nich bude pretekať v kritickom prípade prúd \(I\), takže horná z dvojice poistiek by sa mala prepáliť. V tomto momente však v hlavnej časti obvodu už bude tiecť prúd \(2I\), takže sa môže prepáliť ľubovoľná poistka hlavnej vetvy, čiže v tomto momente je správanie sa obvodu nejednoznačné. Tento variant je na grafe zaznačený čiarkovanou čiarou.

Kvantitatívny rozbor

Začnime tým, že si nájdeme odpor neporušeného súpoistia. Ak poznáme odpor \(R_{n-1}\) predchádzajúcej úrovne, odpor \(R_{n}\) dostaneme z rovnice \[ \frac{1}{R_{n}}=\frac{1}{R_{n-1}+R}+\frac{1}{R}\text{.} \]

Povedali sme, že ak je \(n\) dostatočne veľké, tak \(R_{n}\approx R_{n-1}\overset{\mathrm{ozn.}}{=}R_{\infty}\). Keď to dosadíme do uvedenej rovnice, dostaneme kvadratickú rovnicu pre \(R_{\infty}\) \[ R_{\infty}^{2}+R\cdot R_{\infty}-R^{2}=0\text{,} \] ktorej riešením je \[ R_{\infty}=\frac{\pm\sqrt{5}-1}{2}R\text{.} \]

Kladný koreň dostaneme len pre znamienko „+“, takže \[ R_{\infty}=\frac{\sqrt{5}-1}{2}R\doteq\num{0.618}R\text{.} \]

Tomu zodpovedá prúd \[ I_{\infty}=\frac{U}{R_{\infty}}=\frac{\sqrt{5}+1}{2}\frac{U}{R}\doteq\num{1.618}\frac{U}{R}\text{.} \]

No nie je to božské?!¹

Striktne vzaté sa nám podarilo nájsť odpor nekonečne veľkého súpoistia. Nájdime teraz aj odpor konečne veľkého. Budeme pritom vychádzať z rekurentného vzťahu \[ R_{n+1}=\frac{R_{n}+R}{R_{n}+2R}R\text{.} \]

Skúsme si do tohto výrazu dosadiť vyjadrenie odporu \(R_{n}\) pomocou odporu \(R_{n-1}\). Dostaneme \[ R_{n+1} = \frac{\frac{R_{n-1}+R}{R_{n-1}+2R}R+R}{\frac{R_{n-1}+R}{R_{n-1}+2R}R+2R}R=\frac{2R_{n-1}+3R}{3R_{n-1}+5R}R\text{.} \]

Ak by sme tak urobili znovu, dostali by sme \[ R_{n+1} = \frac{5R_{n-2}+8R}{8R_{n-2}+13R}R\text{.} \]

Už ste si v tom všimli istú pravidelnosť? Opakované vnáranie rekurentného vzťahu vedie k tomu, že v čitateli aj v menovateli sa budú vyskytovať stále väčšie a väčšie Fibonacciho čísla.²

Môžeme sa pokúsiť formalizovať to. Označme \(a_{n}\) \(n\)-té Fibonacciho číslo. Platí \(a_{0}=0\), \(a_{1}=1\) a \(a_{n+1}=a_{n}+a_{n-1}\). Potom možno písať \[ R_{n+1} = \frac{a_{1}R_{n} + a_{2}R}{a_{2}R_{n}+a_{3}R}R=\frac{a_{3}R_{n-1}+a_{4}R}{a_{4}R_{n-1}+a_{5}R}R=\frac{a_{5}R_{n-2}+a_{6}R}{a_{6}R_{n-2}+a_{7}R}R\text{,} \]

čo sa dá zovšeobecniť ako \[ R_{n+1} = \frac{a_{2l+1}R_{n-l}+a_{2l+2}R}{a_{2l+2}R_{n-l}+a_{2l+3}R}R\text{.} \]

Ak teraz použijeme \(l=n-1\), dostaneme \[ R_{n+1} = \frac{a_{2n-1}R_{1}+a_{2n}R}{a_{2n}R_{1}+a_{2n+1}R}R\text{.} \]

Vieme pritom, že \(R_{1}=\frac{R}{2}\), preto \[ R_{n+1} = \frac{a_{2n-1}+2a_{2n}}{a_{2n}+2a_{2n+1}}R,\,n=1,2,3,\dots \] Využijúc rekurentný vzťah Fibonacciho postupnosti \(a_{n+1}=a_{n}+a_{n-1}\) možno tento výraz ešte zjednodušiť: \[ R_{n+1} = \frac{a_{2n-1}+2a_{2n}}{a_{2n}+2a_{2n+1}}R=\frac{a_{2n+1}+a_{2n}}{a_{2n+2}+a_{2n+1}}R=\frac{a_{2n+2}}{a_{2n+3}}R\text{.} \]

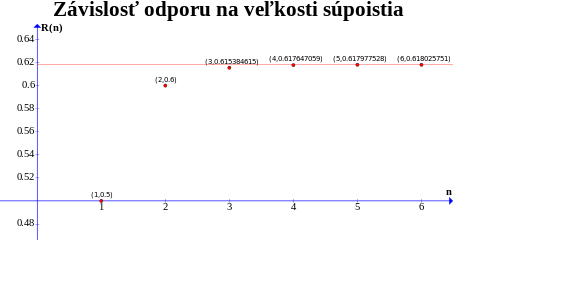
Našli sme vyjadrenie odporu konečne veľkého súpoistia pomocou Fibonacciho čísel. Teraz si môžeme vyčísliť niekoľko prvých odporov, aby sme zistili, aké veľké musí byť súpoistie, aby sa jeho odpor ďalším zväčšovaním už veľmi nemenil. Z grafu okamžite vidíme, že počnúc \(R_{4}\) sa odpor veľmi nemení a že odpor naozaj konverguje k \(R_{\infty}\).. To je však z vyjadrenia \(R_{n}=\frac{a_{2n}}{a_{2n+1}}R,\,n=0,1,2,3,\dots\) zrejmé, keďže \[ R_{\infty}=\lim_{n\rightarrow\infty}R_{n}=\lim_{n\rightarrow\infty}\frac{a_{2n}}{a_{2n+1}}R=\left.\frac{1}{\phi}R\right|_{\phi=\frac{\sqrt{5}+1}{2}}=\frac{\sqrt{5}-1}{2}R\text{.} \]

Teraz nám už nič nebráni vyjadriť hľadaný prúd ako \[ I_{n}=\frac{U}{R_{n}}=\frac{a_{2n+1}}{a_{2n}}\frac{U}{R},\,n=1,2,3,\dots \] To je prúd, ktorý tečie obvodom do momentu, než sa prepáli prvá poistka.

Poďme ďalej skúmať, ako sa zmenia pomery v obvode po prepálení poistiek. Už sme si vysvetlili, v akom poradí sa budú poistky prepaľovať. Nájdime, aký bude odpor súpoistia po prepálení \(k\) poistiek. Označme si tento odpor \(R_{n}^{k}\). V tomto momente bude obvod pozostávať z \(k\) poistiek zapojených v sérii a k nim sériovo pripojeného súpoistia \(\left(n-k\right)\)-tej úrovne, preto celkový odpor bude \[ R_{n}^{k}=kR+R_{n-k}^{0}=\left(k+\frac{a_{2n-2k}}{a_{2n-2k+1}}\right)R\text{.} \]

Nájdime, pri akom prúde sa prepáli \(k\)-ta poistka. Označme si tento prúd \(\hat{I}_{n}^{k}\). Cez vetvu s jedinou poistkou musí v tomto momente tiecť prúd \(I\). Nech druhou vetvou tečie prúd \(\tilde{I}_{n}^{k}\). Podľa prvého Kirchhoffovho zákona platí, žu súčet prúdov vtekajúcich do uzla je rovný súčtu prúdov vytekajúcich z tohto uzla, teda \[ \hat{I}_{n}^{k}=I+\tilde{I}_{n}^{k}\text{.} \]

Zároveň podľa druhého Kirchhoffovho zákona má byť v oboch vetvách rovnaký úbytok napätia, teda \[ IR=\tilde{I}_{n}^{k}\left(R+R_{n-k}^{0}\right)\text{.} \]

Vylúčením nezaujímavého \(\tilde{I}_{n}^{k}\) dostávame \[ \hat{I}_{n}^{k}=\left(1+\frac{R}{R+R_{n-k}^{0}}\right)I\text{,} \]

čo možno opäť vyjadriť pomocou Fibonacciho čísel ako \[ \hat{I}_{n}^{k}=\frac{2a_{2n-2k+1}+a_{2n-2k}}{a_{2n-2k+1}+a_{2n-2k}}I\text{.} \]

Tomuto prúdu zodpovedá napätie \[ U_{n}^{k}=R_{n}^{k-1}\hat{I}_{n}^{k}=\left(k-1+\frac{a_{2n-2k+2}}{a_{2n-2k+3}}\right)\frac{2a_{2n-2k+1}+a_{2n-2k}}{a_{2n-2k+1}+a_{2n-2k}}RI\text{.} \]

Na záver ešte nájdeme prúd \(\bar{I}_{n}^{k}\), ktorý tečie obvodom tesne po prepálení \(k\)-tej poistky \[ \bar{I}_{n}^{k}=\frac{U_{n}^{k}}{R_{n}^{k}}=\frac{R_{n}^{k-1}}{R_{n}^{k}}\hat{I}_{n}^{k}=\frac{k-1+\frac{a_{2n-2k+2}}{a_{2n-2k+3}}}{k+\frac{a_{2n-2k}}{a_{2n-2k+1}}}\frac{2a_{2n-2k+1}+a_{2n-2k}}{a_{2n-2k+1}+a_{2n-2k}}I\text{.} \]

Na záver si vykreslime nájdenú voltampérovú charakteristiku. Tu uvedieme VA charakteristiky pre súpoistia s \(n=10\) a \(n=50\).

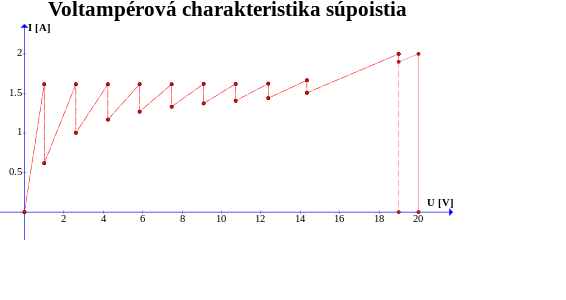
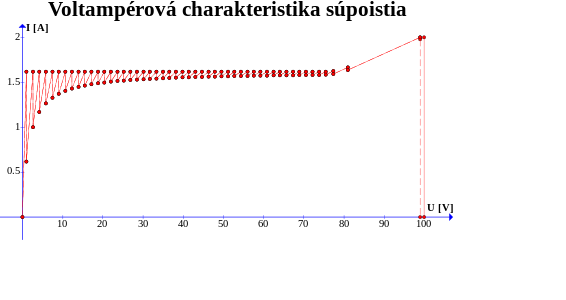
A čo z toho ste mali urobiť? V prvom rade ste si mali uvedomiť, v akom poradí sa budú poistky prepaľovať a ako sa to prejaví na odpore súpoistia, resp. pretekajúcom prúde. Následne ste mohli načrtnúť, ako vyzerá voltampérová charakteristika súpoistia. Čo sa týka nájdenia význačných hodnôt, nemuseli ste nájsť napätia a prúdy pre všeobecné počty použitých poistiek. Stačilo si zvoliť nejaké \(n\) a úlohu riešiť numericky.

---

1. Ale je! Číslo, ktoré sme dostali, má vlastné meno. Označuje sa gréckym písmenom \(\phi\) a nazýva sa zlatý rez alebo niekedy aj božský pomer. Okrem iného je rovný limite pomeru dvoch po sebe nasledujúcich Fibonacciho čísel. To nie je náhoda, ako uvidíme neskôr.↩

2. Na tomto mieste nebudeme matematicky rigorózni a dôkaz neuvedieme.↩