5. Crash course slušného stolovania vzorové riešenie

Zadanie

Pamätá si ešte niekto Vilomeniny? To bola taká tá relácia, na konci ktorej vždy vyťahovali obrus zo stola spod kopy rozložených tanierov a snažili sa rozbiť čo najmenej. Tak si teraz predstavme tanier zanedbateľných rozmerov sediaci na obruse sediacom na stole, prevísajúcom o dĺžku \(L\). Hmotnosť obrusu je \(m\), hmotnosť taniera \(M\), súčiniteľ šmykového trenia medzi stolom a obrusom \(f_1\), medzi obrusom a tanierom \(f_2\) a medzi tanierom a stolom \(f_3\). Akou najmenšou silou by musel súťažiaci ťahať za obrus, aby tanier zostal na stole, ak pôvodne sedel (tanier, nie súťažiaci) na samom okraji stola?

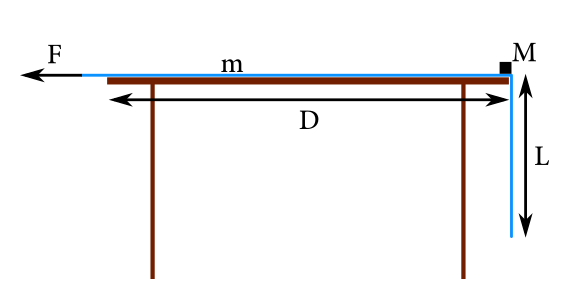
Nuž, aj vám sa zdala táto úloha akási jednoduchá? Veruže aj bola. Ak ste si uvedomili, čo sa v jednotlivých fázach pohybu deje, vystačili ste si s elementárnou mechanikou. Poďme teda na to.

Kľúčom k úspechu bolo rozdeliť si dej na dve etapy. V prvej fáze, kým sa obrus pohybuje pod tanierom, bude na tanier pôsobiť trecia sila konštantnej veľkosti od obrusu, ktorá ho urýchľuje. V momente, keď tanier opúšťa obrus, má už nejakú rýchlosť a začne naň pôsobiť trecia sila od stola, ktorá ho bude naopak spomaľovať.¹ Minimálnu potrebnú silu na vytiahnutie obrusa zrejme dostaneme, keď budeme uvažovať limitný prípad, v ktorom tanier zastane na opačnom konci stola. Keď už toto vieme, stačí nám nájsť príslušné zrýchlenia a dráhy, na ktorých prebiehajú jednotlivé fázy, a sme za vodou. Potom to už bude len o narábaní s rovničkami.

Uvažujme najskôr prvú fázu. Označme zrýchlenie obrusu \(a_{1}\) a zrýchlenie taniera \(a_{2}\). Na tanier pôsobí v horizontálnom smere len trecia sila od obrusu, preto \[ Ma_{2}=f_{2}Mg \quad\Rightarrow\quad a_{2}=f_{2}g\text{.} \]

Na obrus pôsobí okrem trecej sily od taniera ešte aj trecia sila od stola a sila, ktorou obrus ťaháme. Preto môžeme písať \[ ma_{1} = F-f_{2}Mg-f_{1}\left(M+m\right)g \quad\Rightarrow\quad a_{1} = \frac{F}{m}-\left[f_{2}\frac{M}{m}+f_{1}\left(1+\frac{M}{m}\right)\right]g\text{.} \]

Okamžite vidíme, že tak obrus ako i tanier sa pohybujú rovnomerne zrýchleným pohybom.

Nech tanier prejde dráhu \(x=\frac{1}{2}a_{2}t_{1}^{2}\) do momentu, kedy opustí obrus. Ľubovoľný bod obrusu musí za ten istý čas \(t_{1}\) prejsť dráhu \(L+x\), aby sa celý obrus dostal spod taniera. To znamená, že platí \[ L+\frac{1}{2}a_{2}t_{1}^{2} = \frac{1}{2}a_{1}t_{1}^{2}, \]

odkiaľ \[ t_{1}=\sqrt{\frac{2L}{a_{1}-a_{2}}}\text{.} \]

Vylúčením času z vyjadrenia dráhy dostaneme \[ x = \frac{a_{2}L}{a_{1}-a_{2}} \]

a pre rýchlosť taniera v momente opustenia obrusu platí \[ v=a_{2}t_{1}=a_{2}\sqrt{\frac{2L}{a_{1}-a_{2}}}\text{.} \]

Poďme teraz na druhú fázu pohybu. Tá je o poznanie jednoduchšia, lebo žiaden obrus v nej už nefiguruje. Na tanier pôsobí jedine trecia sila od stola proti smeru pohybu, ktorá ho spomaľuje. Možno teda písať² \[ Ma_{3}=f_{3}Mg \quad\Rightarrow\quad a_{3}=f_{3}g\text{.} \]

Tanieru zostáva do konca stola prešmýkať sa vzdialenosť \(D-x\). Vzhľadom na to, že spomaľuje z rýchlosti \(v\) a na konci stola musí zastať, tak možno písať súbor rovníc \[ 0 = v-a_{3}t_{2} \quad\Rightarrow\quad t_{2}=\frac{v}{a_{3}}\text{;} \] \[ D-x = vt_{2}-\frac{1}{2}a_{3}t_{2}^{2} = \frac{v^{2}}{2a_{3}}\text{.} \]

Vylúčením neznámych zrýchlení a dráhy \(x\) postupnými úpravami dostávame \[ D-\frac{a_{2}L}{a_{1}-a_{2}} = \frac{1}{2a_{3}}a_{2}^{2}\frac{2L}{a_{1}-a_{2}}\text{;} \]

\[ a_{1} = a_{2}\left(1+\frac{L}{D}+\frac{a_{2}}{a_{3}}\frac{L}{D}\right)=f_{2}g\left(1+\frac{L}{D}+\frac{f_{2}}{f_{3}}\frac{L}{D}\right)\text{;} \]

\[ F = \left\{ f_{1}\left(M+m\right)+f_{2}\left[M+\left(1+\frac{L}{D}+\frac{f_{2}}{f_{3}}\frac{L}{D}\right)m\right]\right\} g\text{.} \]