2. Romantický moment vzorové riešenie

Zadanie

Simon si tak minule sedel na lavičke v parku, keď tu zrazu si k nemu prisadla veľmi atraktívna slečna. Chcel na ňu urobiť dojem veľmi známou baliacou fintou „vieš, že vzdialenosť odtiaľto sem je rovnaká ako odtiaľto sem?“, avšak nechcel ju svojím rýchlym postupom vyplašiť.

Preto sa k nej začal pomaly posúvať. Po istom čase sa však neprajná lavička prevážila na stranu a Simon aj so slečnou sa z nej zosypali. Kde na lavičke sa v tomto momente Simon hmotnosti \(m_{SI}\) nachádzal, ak si slečna s hmotnosťou \(m_{SL}\) sadla na opačný koniec lavičky? Lavička je osovo súmerná, má hmotnosť \(M\), dĺžku \(L\) a rozostup oporných bodov \(D\).

Pretransformujme zadanie do jazyka fyziky. Tiaž Simona, slečny, ale aj samotnej lavičky vytvára vzhľadom na pravý oporný bod nenulové momenty síl. Spomeňme si, že veľkosť momentu sily vypočítame ako súčin veľkosti pôsobiacej sily a ramena sily. Rameno je jednoducho kolmá vzdialenosť od pôsobiska sily k osi otáčania. Je teda zrejmé, že ak moment sily od slečny \({M}_\mathrm{SL}\), usilujúci sa lavičku prevážiť, prekoná súčet momentov síl od Simona \({M}_\mathrm{SI}\) a lavičky¹ \({M}_\mathrm{T}\), ktoré tejto snahe odporujú, lavička sa preváži. Takže chceme zistiť, pre akú vzdialenosť Simona od slečny \(d\) nastane rovnosť týchto momentov – pre akékoľvek menšie \(d\) sa už lavička preváži.

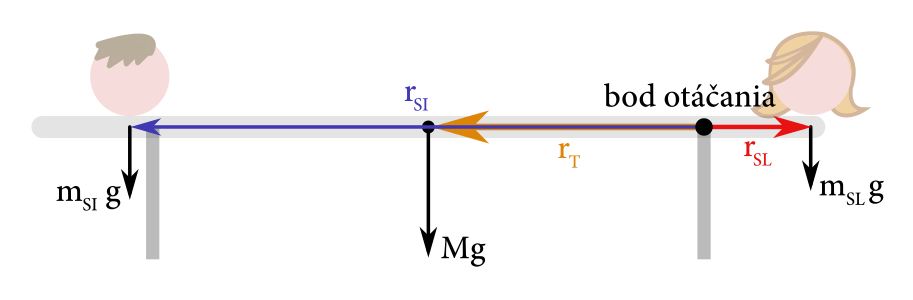
Začnime teda s výpočtom: \[ M_\mathrm{SL} = M_\mathrm{SI} + M_\mathrm{T}, \] \[ m_\mathrm{SL} g r_\mathrm{SL} = m_\mathrm{SI} g r_\mathrm{SI} + M g r_\mathrm{T}\text{.} \]

Nakoľko lavička je osovo súmerná, horizontálna vzdialenosť ťažiska od osi rotácie je \(r_\mathrm{T} = D/2\). Pre jednoduchosť uvažujme, že slečna sedí tak, že jej ťažisko je nad okrajom lavičky.² Dĺžka ramena je \(\frac{L-D}{2}\), a teda \(r_\mathrm{SL} = \frac{L-D}{2}\) a \(r_\mathrm{SI} = d - \frac{L-D}{2}\). Zostáva už len dosadiť \[ m_\mathrm{SL} g \frac{L-D}{2} = m_\mathrm{SI} g \left(d-\frac{L-D}{2}\right) + M g \frac{D}{2} \]

a vyjadriť \(d\) \[ d = \frac{\frac{L-D}{2} g \left(m_\text{SL} + m_\text{SI}\right) - M g \frac{D}{2}}{m_\text{SI} g} = \frac{L \left(m_\text{SL} + m_\text{SI}\right) - D \left(M + m_\text{SL} + m_\text{SI}\right)}{2 m_\text{SI}}\text{.} \]

Takže v momente, keď Simon prekoná kritickú vzdialenosť \[ d = \frac{L \left(m_\mathrm{SL} + m_\mathrm{SI}\right) - D \left(M + m_\mathrm{SL} + m_\mathrm{SI}\right)}{2 m_\mathrm{SI}}\text{,} \] spolu so slečnou sa z lavičky zosypú.

Poznámka pre hĺbavé typy

Mnohí z vás pri riešení delili lavičku na časť naľavo od osi otáčania a napravo od osi otáčania a uvažovali momenty od oboch častí oddelene. Ak budete čítať ďalej, zistíte, prečo je v poriadku uvažovať moment sily od ťažiska, aj keď časť lavičky sa nachádza naľavo a časť napravo od osi rotácie. Celkový moment sily lavičky sa dá vypočítať tak, že rozdelíme lavičku na veľa maličkých častí s polohami \(x_i\) a hmotnosťami \(m_i\)³ a celkový moment sily vypočítame ako súčet momentov sily od všetkých týchto častí. Takže ak poloha bodu otáčania je \(x_\mathrm{O}\), celkový moment sily bude \[ M_\mathrm{T} = \sum m_i g \left(x_i - x_\mathrm{O}\right). \]

Keď si spomenieme na vzťah pre polohu ťažiska \(x_T = \frac{\sum x_i m_i}{M}\), celkový moment sily môžeme upraviť na \[ M_\mathrm{T} = \sum m_i g \left(x_i - x_\text{O}\right) = g\sum m_i x_i - gx_\mathrm{O} \sum m_i = Mg\frac{\sum x_i m_i}{M} - Mgx_\mathrm{O} = Mg\left(x_\mathrm{T} - x_\mathrm{O}\right)\text{,} \]

čo nie je nič iné ako moment sily od ťažiska. Takže ak poznáme polohu ťažiska, celý výpočet si môžeme uľahčiť bez akéhokoľvek porušovania fyziky.