7. Hviezdny valčík vzorové riešenie

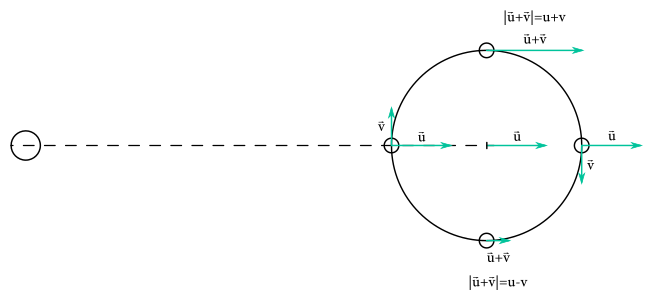
Prvá vec, ktorú si musíme uvedomiť, je dôvod, prečo Kvík pozoruje v rozličných postaveniach hviezd rozličné frekvencie tej istej spektrálnej čiary. Po chvíľke dumania prídeme na to, že jediným rozumným vysvetlením je Dopplerov jav v spojení s tým, aký pohyb hviezdy vykonávajú. Tie totiž obiehajú okolo spoločného ťažiska rýchlosťou \(v\), ktoré sa navyše od Zeme vzďaľuje rýchlosťou \(u\). Keď sú teda obe hviezdy a Zem na jednej priamke, obe hviezdy sa od Zeme pohybujú rýchlosťou \(u\). Keď je spojnica hviezd kolmá na smer k Zemi, vtedy sa jedna z hviezd pohybuje vzhľadom na Zem rýchlosťou \(u+v\) a druhá rýchlosťou \(u-v\). To je dôvodom, prečo Kvík pozoruje dvojicu spektrálnych čiar.

Keď sme prišli na príčinu rozdielov vo frekvencii tej istej spektrálnej čiary, môže sa zdať, že už máme vyhraté. Stačí to už len nahádzať do rovníc a vybúchať z nich rýchlosť \(u\). Alebo žeby nie? Pripomeňme, že zmenu frekvencie pri Dopplerovom jave popisuje rovnica \[ f' = f\,\frac{c\pm w_{r}}{c\pm w_{s}}\text{,} \qquad(1)\]

kde \(c\) je rýchlosť vlnenia, \(w_{r}\) je rýchlosť pozorovateľa (receiver) a \(w_{s}\) je rýchlosť zdroja (source). Znamienka vyberáme podľa toho, ktorým smerom sa pozorovateľ a zdroj pohybujú. Prípustné sú všetky štyri kombinácie.

V našom prípade je \(c\) rýchlosť svetla. Ale čo sú naše rýchlosti \(w_{r}\) a \(w_{s}\)? Na prvý pohľad je zjavné, že výsledok závisí na voľbe vzťažnej sústavy. Otázka znie, ako volíme vzťažnú sústavu. Aby sme si na to zodpovedali, uvažujme názornejší príklad – dve autá pohybujúce sa oproti sebe. Vtedy máme na výber vzťažné sústavy spojené s jednotlivými autami, s babkou stojacou na zastávke či s Jožkom utekajúcim na autobus, ale aj akúkoľvek inú vzťažnú sústavu.

Niekomu by mohlo napadnúť, že vzťažnú sústavu volíme podľa toho, o kým pozorovanú frekvenciu sa zaujímame, teda ak nás zaujíma, akú frekvenciu počuje babka, tak situáciu popisujeme v babkinej sústave. Ale čo potom vo vzťahu 1 robí rýchlosť \(w_r\), keď tá by musela byť vždy nulová? Tá rýchlosť tam nebude len tak, a preto táto voľba nemôže byť správna.

V skutočnosti volíme vzťažnú sústavu spojenú s prostredím, v ktorom sa vlnenie šíri. V prípade zvuku je tým prostredím vzduch. A čo v prípade svetla? Teória relativity hovorí, že svetlo sa vo všetkých vzťažných sústavách šíri rovnako, teda v prípade svetla výsledok nemôže závisieť na voľbe vzťažnej sústavy. To je však v rozpore so vzťahom 1, preto ten nemôže popisovať Dopplerov jav pre svetlo.

Vzťah 1 je odvodený na základe Galileiho transformácií, ktoré sú nerelativistické. Keby sme využili relativistické Lorentzove transformácie, dostali by sme odlišný vzťah \[ f'=f\sqrt{\frac{c\pm w}{c\mp w}}\text{.} \qquad(2)\]

Jeho odvodenie tu nebudeme vykonávať, keďže čitateľ si ho vie jednoducho vyhľadať v dostupnej literatúre či na webe. Len poznamenajme, že v čitateli aj v menovateli vystupuje rovnaká rýchlosť \(w\), ktorá je vzájomnou rýchlosťou zdroja a pozorovateľa, preto výsledok nezávisí na voľbe vzťažnej sústavy. V tomto prípade sú prípustné len dve kombinácie znamienok – vždy vyberáme rozdielne znamienka, pričom ich voľba závisí na tom, či sa objekty od seba vzďaľujú alebo či sa k sebe približujú.

Tú zaujímavejšiu časť úlohy máme za sebou. Teraz sa už môžeme pustiť do počítania. Nech je skutočná frekvencia spektrálnej čiary \(f\). Pre pozorované frekvencie potom platí \[\begin{aligned} f_+^{\text{ 2}} &= f^{\text{ 2}} \frac{c-\left(u+v\right)}{c+\left(u+v\right)}\text{,} \\ f_-^{\text{ 2}} &= f^{\text{ 2}} \frac{c-\left(u-v\right)}{c+\left(u-v\right)}\text{,} \\ f_0^{\text{ 2}} &= f^{\text{ 2}} \frac{c-u}{c+u}\text{.} \end{aligned}\qquad(3)\]

Vylúčme zo sústavy rovníc skutočnú frekvenciu spektrálnej čiary \(f\) predelením prvých dvoch rovníc v  3 treťou. Po niekoľkých jednoduchých úpravách sa dopracujeme do tvaru \[\begin{aligned} f_+^{\text{ 2}} \left(u^2+uv-cv-c^2\right) & = f_0^{\text{ 2}}\left(u^{2}+uv+cv-c^{2}\right)\text{,}\\ f_-^{\text{ 2}} \left(u^2-uv+cv-c^2\right) & = f_0^{\text{ 2}}\left(u^{2}-uv-cv-c^{2}\right)\text{.} \end{aligned}\qquad(4)\]

Vidíme, že obe rovnice sú lineárne vo \(v\) a kvadratické v \(u\). Zaujímame sa o rýchlosť vzďaľovania dvojhviezdy \(u\), preto z oboch rovníc vyjadrime obežnú rýchlosť hviezd \(v\): \[ v = \frac{\left(u^2-c^2\right)\left(f_{0}^{\text{ 2}}-f_{+}^{\text{ 2}}\right)}{f_{+}^{\text{ 2}}\left(u-c\right)-f_{0}^{\text{ 2}}\left(u+c\right)}\text{,}\\ \qquad(5)\]

\[ v =\frac{\left(u^{\text{ 2}}-c^{2}\right)\left(f_{0}^{\text{ 2}}-f_{-}^{\text{ 2}}\right)}{f_{-}^{\text{ 2}}\left(c-u\right)+f_{0}^{\text{ 2}}\left(c+u\right)}\text{.} \qquad(6)\]

Veľmi nás teší, že v oboch rovniciach sa vyskytuje rovnaký faktor \(\left(u^{2}-c^{2}\right)\), pretože keď rovnice medzi sebou predelíme, tento faktor z nich vypadne, čím sa efektívne zníži stupeň rovnice z kubickej na lineárnu. Postupnými úpravami dospejeme ku konečnému výsledku \[ u=\frac{f_{+}^{\text{ 2}}f_{-}^{\text{ 2}}-f_{0}^{\text{ 4}}}{\left(f_{+}^{\text{ 2}}-f_{0}^{\text{ 2}}\right)\left(f_{-}^{\text{ 2}}-f_{0}^{\text{ 2}}\right)}c\text{.} \qquad(7)\]

Niekoho by mohlo napadnúť, že vzájomné rýchlosti hviezd a Zeme sú veľmi malé v porovnaní s rýchlosťou svetla, preto by malo byť možné vzťah 2 linearizovať. Aplikujme naň Taylorov rozvoj \[ f' = f\sqrt{\frac{c-w}{c+w}}=f\sqrt{\frac{1-\frac{w}{c}}{1+\frac{w}{c}}}=f\left(1-\frac{w}{c}+\frac{1}{2}\left(\frac{w}{c}\right)^{2}+\bar{\mathit{o}}\left(\left(\frac{w}{c}\right)^{2}\right)\right)\text{.} \]

Uvažujme najskôr rozvoj len do prvého rádu. V takom prípade dostaneme sústavu rovníc \[\begin{aligned} f_{+} & =f\left(1-\frac{u+v}{c}\right)\text{,}\\ f_{-} & =f\left(1-\frac{u-v}{c}\right)\text{,}\\ f_{0} & =f\left(1-\frac{u}{c}\right)\text{.} \end{aligned}\]

Okamžite vidíme, že táto sústava je ekvivalentná použitiu klasického Dopplera vo vzťažnej sústave zdroja vlnenia. Keď ju však začneme riešiť, narazíme na problém, pretože z nej vypadnú všetky rýchlosti a dostaneme len podmienku pre frekvencie \[ f_{0}=\frac{f_{+}+f_{-}}{2}\text{,} \]

ktorá hovorí, že v priblížení do prvého rádu musí byť frekvencia \(f_{0}\) aritmetickým priemerom zvyšných dvoch.

Aby sme sa dopracovali k nejakému výsledku, musíme teda uvažovať Taylorov rozvoj až do druhého rádu: \[\begin{aligned} f_{+} & =f\left(1-\frac{u+v}{c}+\frac{\left(u+v\right)^{2}}{2c^{2}}\right)\text{,}\\ f_{-} & =f\left(1-\frac{u-v}{c}+\frac{\left(u-v\right)^{2}}{2c^{2}}\right)\text{,}\\ f_{0} & =f\left(1-\frac{u}{c}+\frac{u^{2}}{2c^{2}}\right)\text{.} \end{aligned}\]

Opäť z rovníc vylúčime frekvenciu \(f\) predelením rovníc medzi sebou: \[\begin{aligned} \frac{f_{+}}{f_{0}} & =\frac{2c^{2}-2uc-2vc+u^{2}+v^{2}+2uv}{2c^{2}-2uc+u^{2}}\text{,}\\ \frac{f_{-}}{f_{0}} & =\frac{2c^{2}-2uc+2vc+u^{2}+v^{2}-2uv}{2c^{2}-2uc+u^{2}}\text{.} \end{aligned}\]

Tentokrát sme dostali o čosi komplikovanejšiu sústavu, keďže obe rovnice sú kvadratické v \(u\) i vo \(v\). Nás však nič tak ľahko nezastraší. Pozrieme sa na ne naším odborným okom a hneď vidíme, že keď ich sčítame a odčítame medzi sebou, tak sa o čosi zjednodušia: \[\begin{aligned} \frac{f_{+}+f_{-}}{f_{0}} & =\frac{4c^{2}-4uc+2u^{2}+2v^{2}}{2c^{2}-2uc+u^{2}}\text{,}\\ \frac{f_{+}-f_{-}}{f_{0}} & =\frac{-4vc+4uv}{2c^{2}-2uc+u^{2}}\text{.} \end{aligned}\]

Z týchto rovníc už nie je problém vyjadriť obežnú rýchlosť \(v\) v relatívne jednoduchom tvare: \[\begin{aligned} \left|v\right| & =\sqrt{\left(\frac{f_{+}+f_{-}}{2f_{0}}-1\right)\left(2c^{2}-2uc+u^{2}\right)}\text{,}\\ v & =\frac{\left(f_{+}-f_{-}\right)\left(2c^{2}-2uc+u^{2}\right)}{4f_{0}\left(u-c\right)}\text{.} \end{aligned}\]

Aby sme sa zbavili absolútnej hodnoty a odmocniny, dajme do rovnosti kvadráty obežnej rýchlosti. Dopracujeme sa ku rovnici, ktorá je kvadratická v \(u\) a neobsahuje rýchlosť \(v\), a teda už nemáme najmenší problém nájsť riešenie: \[\begin{gathered} u^{2}-2cu+\frac{8f_{0}\left(f_{+}+f_{-}-2f_{0}\right)-2\left(f_{+}-f_{-}\right)^{2}}{8f_{0}\left(f_{+}+f_{-}-2f_{0}\right)-\left(f_{+}-f_{-}\right)^{2}}c^{2}=0\text{,}\\ u=c\left(1\pm\sqrt{1-\frac{8f_{0}\left(f_{+}+f_{-}-2f_{0}\right)-2\left(f_{+}-f_{-}\right)^{2}}{8f_{0}\left(f_{+}+f_{-}-2f_{0}\right)-\left(f_{+}-f_{-}\right)^{2}}}\right)\text{.} \end{gathered}\]

Fyzikálne riešenie je to so znamienkom mínus, keďže \(\left|u\right|\overset{!}{<}c\). Pozorný čitateľ by mohol namietať, že náš výsledok nemôže byť správny, pretože narábame s relativistickým Dopplerovým javom a pritom sme použili klasický vzťah na skladanie rýchlostí. A má v podstate pravdu. V skutočnosti by sme mali uvažovať relativisticky získané rýchlosti vzďaľovania jednotlivých hviezd \[ w_{\pm}=\frac{u\pm v}{1\pm\frac{uv}{c^{2}}}\text{.} \] Avšak vzhľadom na to, že rýchlosti \(u\) i \(v\) sú malé v porovnaní s rýchlosťou svetla, hohlo by sa zdať, že si môžeme dovoliť použiť aj klasicky zložené rýchlosti. Pozrime sa však na to, k akému výsledku by sme sa dopracovali, keby sme predsa len použili relativistický vzťah na skladanie rýchlostí, pretože je to vskutku zaujímavé. Budeme nasledovať úplne rovnaký postup ako v prvom prípade. Vychádzame zo sústavy rovníc \[\begin{aligned} f_{+}^{\text{ 2}} & =f^{\text{ 2}}\frac{c-\frac{u+v}{1+\frac{uv}{c^{2}}}}{c+\frac{u+v}{1+\frac{uv}{c^{2}}}}\text{,}\\ f_{-}^{\text{ 2}} & =f^{\text{ 2}}\frac{c-\frac{u-v}{1-\frac{uv}{c^{2}}}}{c+\frac{u-v}{1-\frac{uv}{c^{2}}}}\text{,}\\ f_{0}^{\text{ 2}} & =f^{\text{ 2}}\frac{c-u}{c+u}\text{.} \end{aligned}\]

Vylúčením frekvencie \(f\) dostaneme \[\begin{aligned} f_{+}^{\text{ 2}}\left(u^{2}+\frac{u^{2}v}{c}-cv-c^{2}\right) & =f_{0}^{\text{ 2}}\left(u^{2}-\frac{u^{2}v}{c}+cv-c^{2}\right)\text{,}\\ f_{-}^{\text{ 2}}\left(u^{2}-\frac{u^{2}v}{c}+cv-c^{2}\right) & =f_{0}^{\text{ 2}}\left(u^{2}+\frac{u^{2}v}{c}-cv-c^{2}\right)\text{.} \end{aligned}\]

Z rovníc vieme vyjadriť obežnú rýchlosť \[\begin{aligned} v & =\frac{\left(f_{0}^{\text{ 2}}-f_{+}^{\text{ 2}}\right)\left(c^{2}-u^{2}\right)}{\left(f_{+}^{\text{ 2}}+f_{0}^{\text{ 2}}\right)\left(c-\frac{u^{2}}{c}\right)}\text{,}\\ v & =\frac{\left(f_{0}^{\text{ 2}}-f_{-}^{\text{ 2}}\right)\left(c^{2}-u^{2}\right)}{\left(f_{-}^{\text{ 2}}+f_{0}^{\text{ 2}}\right)\left(\frac{u^{2}}{c}-c\right)}\text{.} \end{aligned}\]

Keď dáme tieto výrazy do rovnosti, dospejeme k rovnici, ktorá neobsahuje žiadne rýchlosti \[ \frac{f_{0}^{\text{ 2}}-f_{+}^{\text{ 2}}}{f_{0}^{\text{ 2}}+f_{+}^{\text{ 2}}}+\frac{f_{0}^{\text{ 2}}-f_{-}^{\text{ 2}}}{f_{0}^{\text{ 2}}+f_{-}^{\text{ 2}}}=0\text{,} \] čo sa dá ešte zjednodušiť na \[ f_{0}=\sqrt{f_{+}f_{-}}\text{,} \] takže frekvencia \(f_{0}\) by mala byť geometrickým priemerom zvyšných dvoch. Čo to znamená? Ak neurobíme žiadne zanedbania, tak principiálne nie je možné určiť rýchlosť vzďaľovania dvojhviezdy. Po hlbšom zamyslení nás to však veľmi neprekvapuje. Máme totiž vlnenie nejakej frekvencie a zaujíma nás, ako sa táto frekvencia zmení vplyvom Dopplerovho javu. Zmena frekvencie je jednoznačne daná rýchlosťami \(u\) a \(v\). Ak teda poznáme zdanlivé frekvencie v dvoch prípadoch, frekvenciu v treťom prípade vieme dopočítať použitím posledne odvodeného vzťahu. To znamená, že naša trojica rovníc, z ktorej sme vychádzali, nebola nezávislá, a teda z nej nie je možné dopočítať tri neznáme, keďže efektívne máme len dve rovnice. Znamená to, že Doppler nám nevie nič povedať o rýchlosti vzďaľovania dvojhviezdy? Nie, ak nevieme, aká je skutočná frekvencia pozorovanej spektrálnej čiary. Ale vzhľadom na to, že frekvencie spektrálnych čiar sú známe, tak v praxi nám stačí identifikovať danú spektrálnu čiaru a použitím dvoch zdanlivých frekvencií dopočítať rýchlosť vzďaľovania dvojhviezdy.

Poznámka od riešiteľa

Česť a sláva patrí Jonášovi, ktorý ako jediný poctivým relativistickým výpočtom ukázal, že z pozorovaných frekvencií nie je možné určiť rýchlosť vzďaľovania dvojhviezdy. Použil šikovný trik, keď uvažoval pomocný objekt pohybujúci sa spolu s ťažiskom dvojhviezdy, no a potom zrátal dvojnásobný dopplerovský posun. Prvý posun zohľadnil obežnú rýchlosť hviezd a druhý rýchlosť pohybu ťažiska dvojhviezdy od Zeme. Tento výpočet viedol na vzťah medzi pozorovanými frekvenciami \[ f_{0}=\frac{2f_{+}f_{-}}{f_{+}+f_{-}}\text{,} \]

ktorý sa líši od toho, ktorý sme dostali my. Problém je v tom, že my sme v prípade pozorovanej frekvencie \(f_0\) uvažovali, že rýchlosť vzďaľovania hviezdy je \(u\), čo však nie je pravda. V skutočnosti musíme relativisticky zložiť kolmé rýchlosti \(u\) a \(v\) a takto získanú rýchlosť použiť vo vzťahu pre relativistického Dopplera.