5. Ozembuch vzorové riešenie

Zadanie

Po tom, čo Majka zmerala hustotu svojho dreveného valca, rozhodla sa, že sa s ním naučí trochu žonglovať. Položila si ho na svoju dokonale rovnú ruku dĺžky \(l\) a bez prešmykovania ho nechala skotúľať sa a spadnúť na zem. S tou sa valček nepružne zrazil. Majka chce dosiahnuť, aby mal valček na zemi po ustálení čo najvyššiu rýchlosť. Pod akým uhlom musí ruku nakloniť? Majkino zápästie je vo výške \(h\), valček má hmotnosť \(m\) a polomer \(r\), koeficient trenia medzi zemou a valčekom je \(f\). Valivý odpor neuvažujeme.

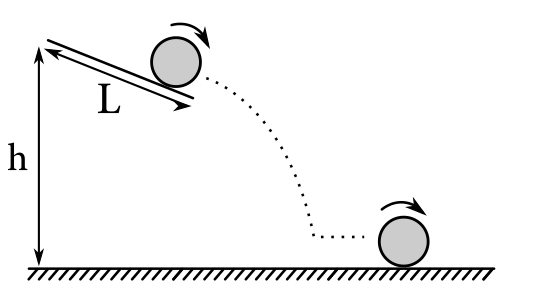
Celú situáciu môžeme popísať nasledovne:

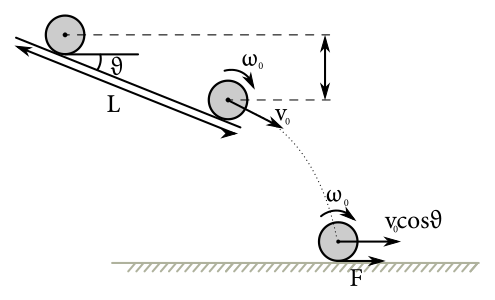
Označme si \(\theta\) uhol, ktorý zviera Majkina ruka s vodorovným smerom, t. j. pre \(\theta=\SI{0}{\degree}\) je vo vodorovnej polohe. Zadanie nám hovorí, že počas pohybu na ruke valec istotne neprešmykuje. Neprešmykovanie znamená, že okraj valca a povrch ruky sa navzájom nepohybujú, a teda trecia sila nekoná na valci prácu. To nám vcelku spríjemňuje život umožnením použitia zákona zachovania energie na zistenie rýchlosti a uhlovej rýchlosti, ktoré si valec z ruky odnesie: \[ \Delta E = \Delta E_{\mathrm{pot}} + \Delta E_{\mathrm{pos.}} + \Delta E_{\mathrm{rot.}}=0\text{.} \] \[ -mgL\sin{\theta}+\frac{1}{2}mv_0^2+\frac{1}{2}I\omega_0^2=0\text{.} \]

Neprešmykovanie nám tiež hovorí, že posuvná a uhlová rýchlosť sú spriahnuté cez polomer valca ako \[ v_0=\omega_0 r \]

a moment zotrvačnosti valca okolo vlastnej osi je \(I=\frac{1}{2}mr^2\). Dostávame teda \[ \frac{3}{4}mv_0^2 = mgL\sin{\theta}\text{.} \]

Keďže zadanie sa nás pýta len na optimálny uhol, potrebujeme poznať jedine závislosť \(v_0\) od \(\theta\). Predchádzajúca rovnica nám prezrádza, že \[ v_0\propto\sqrt{\sin{\theta}}\text{.} \]

Počas letu sa valčeku nemení ani uhlová, ani vodorovná zložka posuvnej rýchlosti. Meniaca sa zvislá zložka rýchlosti je teda počas letu jedinou vzrušujúcejšou udalosťou. Čo sa však stane s valčekom po dopadnutí? Nepochybne sa zbaví zvislej zložky rýchlosti. Najjednoduchší prístup je na ňu jednoducho zabudnúť, čo však nie je vcelku korektný prístup. Každá zmena hybnosti je krytá pôsobiacou silou, alebo presnejšie povedané impulzom sily. A ako v riadnej sústave tento impulz reakčnej sily podložky značí aj impulz (momentu) trecej sily. Žiaľ, keďže takéto riešenie vyžaduje kvôli svojej všeobecnej analytickej neriešiteľnosti konkrétne hodnoty zadaných veličín, musí sa čitateľ uspokojiť s nie úplne správnym postupom a viac bodmi. Zabudnime teda na vodorovnú zložku rýchlosti a riešme ďalej.

Tesne po dopadnutí máme po novom valček s rýchlosťou \(v_0\cos{\theta}\) a uhlovou rýchlosťou \(\omega_0=\frac{v_0}{r}\). Keďže sa tieto hodnoty líšia nie faktorom \(\frac{1}{r}\), ale \(\frac{\cos{\theta}}{r}\), s istotou vieme, že valček bude po dopade prešmykovať. Obvodová rýchlosť valčeka (\(\omega r\)) je na začiatku nutne väčšia než jeho posuvná rýchlosť \(v\). To značí, že na spodku valčeka nám bude pôsobiť trecia sila \(F\) v smere pohybu valčeka. Zároveň však moment tejto sily \(N=Fr\) bude pribrzďovať rotáciu valčeka. Naša dvojica rovníc teda vyzerá takto: \[ v=v_0\cos{\theta}+\frac{F}{m}t\text{,} \] \[ \omega=\omega_0-\frac{Fr}{I}t\text{.} \]

Rozpísaním momentu zotrvačnosti v druhej rovnici a jej prenásobením \(r\) dostaneme pre obvodovú rýchlosť vzťah \[v_{\mathrm{obv.}}=\omega r=v_0-2\frac{F}{m}t\text{.}\]

Vieme, že výsledná posuvná rýchlosť valčeka musí byť rovnaká ako jeho obvodová, teda taká, že \(v=v_{\mathrm{obv.}}\). Prenásobme teda prvú rovnicu dvoma a sčítajme ju s druhou. Pre nás zaujímajúce časy to dopadne takto: \[ 3v=v_0\left(1+2\cos{\theta}\right)\text{.} \]

A teda pre konečnú rýchlosť valčeka na podložke platí vo vzťahu k \(\theta\) \[ v\propto\sqrt{\sin{\theta}}\left(1+2\cos{\theta}\right)\text{.} \]

Hľadať maximum tejto funkcie bez derivovania nie je žiadna slasť, avšak vykreslením grafu vieme celkom presne a pohodlne určiť, že valček dosiahne maximálnu rýchlosť pre \(\theta=\ang{42.5}\).