6. Tak určiteee! vzorové riešenie

Zadanie

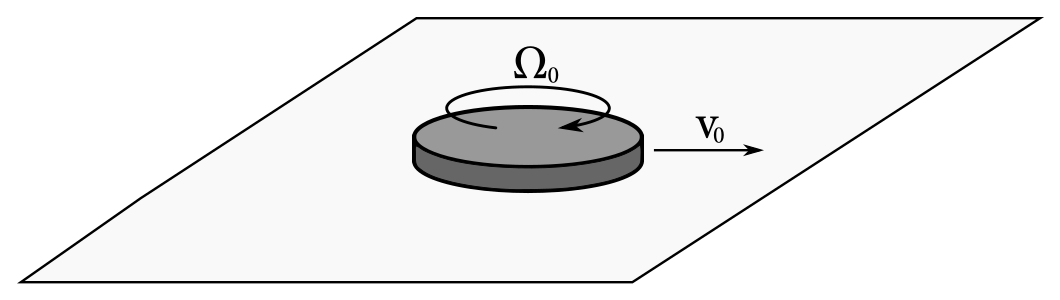
Homogénny puk sa vydal na cestu postupnou rýchlosťou \(v_0\) po vodorovnej drsnej podložke. Cieľom bola bránka na jej konci. Puk videl približujúcu sa bránku a tešil sa, ako v nej skončí. Tu mu však cestu zastal zlomyseľný prst a štuchol doň tak, že mu udelil uhlovú rýchlosť \(\omega_0\) a postupná rýchlosť puku sa nezmenila. Puk po čase zastal a bol z toho veľmi rozladený. Zistite, či by puk bol zastal skôr alebo neskôr, keby doň prst neštuchol, teda keby \(\omega_0=0\).

Bonus: Vypočítajte ako dlho bude trvať, kým puk zastane, ak koeficient šmykového trenia je \(f\) a ak na začiatku \(v_0 \neq 0\) a \(\omega_0 \neq 0\).

Na to, aby sme zistili, či puk zastane skôr alebo neskôr, keď je roztočený sa musíme pozrieť na to, čo sa deje s trecou silou v oboch prípadoch. Nebudeme otáľať a bez zbytočných kecov sa pustíme smelo do riešenia.

Prvú vec, ktorú si musíme uvedomiť, je to, že keďže sa puk nedotýka podložky len v jednom bode, ale celou svojou plochou, tiaž puku sa rovnomerne rozkladá na celú styčnú plochu. To ale znamená, že trecia sila nepôsobí iba v jednom bode, ale môžeme hovoriť o akomsi „trecom šmykovom napätí“. Čo tým chcel autor vzoráku povedať? Predstavme si, že celá styčná plocha puku je \(S\) a pozrime sa na maličkú plôsku veľkú \(\Delta S\), potom trecia sila pôsobiaca v tomto bode je veľká \(mgf \frac{\Delta S}{S}\) a má smer proti smeru rýchlosti, ktorou sa pohybuje maličká plôška \(\Delta S\).

Ak puk nerotuje, každý bod puku sa pohybuje rovnakým smerom a v každom bode má trecia sila rovnaký smer. Akonáhle však puk začne rotovať, tak rýchlosť rôznych bodov na puku bude smerovať rôznym smerom, čo nám dáva nádej na to, že celková trecia sila pôsobiaca proti smeru posuvnému pohybu bude menšia ako v prípade keď puk nerotuje. Skúsme si toto tvrdenie teraz dokázať. Pre jednoduchosť sa pozrime miesto puku tvaru kruhu iba na obruč tvaru kružnice, ktorá sa pohybuje po drsnej podložke. Naše zistenia už potom ľahko zovšeobecníme na celý puk.

Označme si rýchlosť posuvného pohybu \(v\) a uhlovú rýchlosť obruče \(\omega\). Pozrime sa teraz na vektor rýchlosti bodu, ktorý v súradnicovej sústave zviera s osou x uhol \(\phi\).

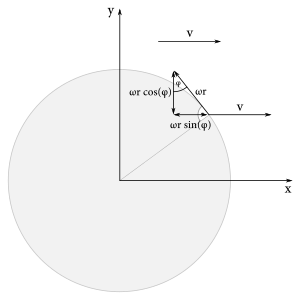
Posuvná rýchlosť v tomto bode je \[ \vec{v_p} = \begin{bmatrix} v \\ 0\end{bmatrix}\text{,} \]

a obvodová rýchlosť rotačného pohybu \[ \vec{v_r} = \begin{bmatrix} -\omega r\sin(\alpha) \\ \omega r\cos(\alpha) \end{bmatrix}\text{.} \]

Celkový vektor rýchlosti v danom bode je potom daný vektorom \[ \vec{v} = \vec{v_p} + \vec{v_r} = \begin{bmatrix} v-\omega r\sin(\alpha) \\ \omega r\cos(\alpha) \end{bmatrix}\text{.} \]

Trecia sila potom pôsobí proti smeru tohto vektora, čiže v opačnom smere ako jednotkový vektor daný vektorom celkovej rýchlosti v danom bode \(\vec{n} = \vec{v}/|\vec{v}|\).

Príspevok trecej sily od kúska kružnice nachádzajúcej sa pod uhlom \(\phi\) je teda \[ \vec{\Delta F_t} = -fmg \frac{\Delta \phi}{2\pi} \vec{n} = -fmg \frac{\Delta \phi}{2\pi} \frac{\left(v - \omega r\sin\alpha, \omega r\cos\alpha\right)}{v^2+\omega^2r^2 -2v\omega r\sin\alpha}\text{.} \]

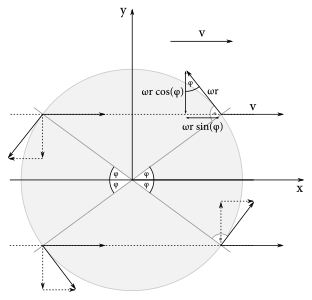
Už sme skoro na konci, teraz si len musíme uvedomiť, že na kružnici sú presne štyri rôzne body, ktoré v absolútnej hodnote rovnakú veľkosť sínusu resp. kosínusu uhla. Ide o uhly \(\phi\), \(\pi - \phi\), \(\pi + \phi\) a \(-\phi = 2\pi - \phi\) (túto množinu uhlov si označme ako \(M\)). Po krátkom zamyslení prídeme na to, že keď pre každú hodnotu \(\phi\) z intervalu \((0\text{,}\pi/2)\) vektorovo spočítame príspevky trecej sily prichádzajúce od týchto štyroch uhlov, tak získame vektor, ktorý má nenulovú len x-ovú komponentu t.j. v proti smeru posuvného pohybu. \[ \sum_{\alpha \in \textbf{M}} \vec{\Delta F_t} = -fmg \frac{4 \Delta \phi}{2\pi} \frac{\left(v, 0\right)}{v^2+\omega^2r^2 -2v\omega r\sin\alpha}\text{.} \]

Môžeme si všimnúť, že ľubovoľne malá nenulová \(\omega\) potom spôsobí, že súčet príspevkov od týchto štyroch bodov na kružnici je menší, ako keby kružnica nerotovala (kvôli členom v menovateli). To potom spôsobí, že aj súčet cez všetky možné uhly od \(\phi\) dopadne tak, že celková trecia sila je menšia pre \(\omega \neq 0\). Napokon si len rozmyslime, že polomer kružnice tu nehrá žiadnu dôležitú úlohu, ak je \(\omega \neq 0\), tak je jedno aký je polomer, výsledná trecia sila je vždy menšia ako v prípade ak by kružnica nerotovala. Výsledok možno preto jednoducho zovšeobecniť na prípad veľa koncentrických kružníc, čiže kruh.

Ak by chcel niekto spočítať celkovú treciu silu pôsobiacu na puk, dopracuje sa k tomuto integrálu, ktorý žiaľ sa nedá už vyjadriť pomocou funkcií, ktoré Vás stredoškolákov alebo nás vysokoškolákov učia v škole (hoc uznajte, s eliptickými integrálmi sa človek nestretáva každý deň, aj keď…). Preto vyriešiť úlohu, akú dráhu puk presne prejde, kým zastane, nie je úloha, ktorá sa dá vyriešiť len pomocou pera a papiera (analyticky). Ak sa však niekto na to dal, napr. numericky, mohol získať oproti štandardným 9 bodom ešte tri bonusové naviac, čiže celkovo získať 12 bodov za túto úlohu!¹

Pre fajnšmekrov teda sľúbený vzorček nakoniec, \[ F_t = -\frac{fmg}{\pi R^2} \int_{0}^{R}\mathrm{d}r\int_{0}^{2\phi}\mathrm{d}\phi \frac{\left(v - \omega r\sin\alpha, \omega r\cos\alpha\right)}{v^2+\omega^2r^2 -2v\omega r\sin\alpha}\text{.} \]