2. Tá blbšia blcha vzorové riešenie

Stanovme si nulovú hladinu potenciálnej energie vo výške, v ktorej sa nachádza blcha. Pred skokom nemá žiadnu energiu. Energia, ktorú musí blcha vyvinúť na jeden skok, je \(E = \frac{1}{2}mv^{2}\). Hľadáme minimálne \(E\) potrebné na doskočenie na okraj ďalšieho schodu, lebo naša blcha je lenivá a chce minúť minimum energie. Hmotnosť má konštantnú, teda hľadáme minimálne \(v^{2}\).

Uvažujme, že blcha skáče pod uhlom \(\alpha\). Napíšme si pohybové rovnice vo vodorovnom a zvislom smere:

\[v\cos(\alpha)t = h\text{,}\] \[v\sin(\alpha)t - \frac{gt^{2}}{2} = h\text{.}\]

Vyjadrime si z prvej rovnice \(t\): \[t = \frac{h}{v\cos(\alpha)}\text{.}\]

Dosaďme za \(t\) do druhej rovnice a upravíme: \[h\frac{\sin(\alpha)}{\cos(\alpha)} - \frac{gh^{2}}{2v^{2}cos^{2}(\alpha)} = h\text{,}\] \[\sin(\alpha) - \cos(\alpha) = \frac{gh}{2v^{2}cos(\alpha)}\text{,}\] \[\sin(\alpha)\cos(\alpha) - \cos^{2}(\alpha)= \frac{gh}{2v^{2}}\text{.}\]

Nakoniec si vyjadríme \(v^{2}\): \[v^{2} = \frac{gh}{2}\frac{1}{\sin(\alpha)\cos(\alpha) - \cos^{2}(\alpha)}\text{.}\]

Keďže \(g\) a \(h\) sú konštanty, tak pre minimálne \(v^{2}\) musíme nájsť maximum funkcie \(\sin(\alpha)\cos(\alpha) - \cos^{2}(\alpha)\) na intervale \(\left(\ang{0};\ang{90}\right)\). Maximum môžeme nájsť napríklad graficky.

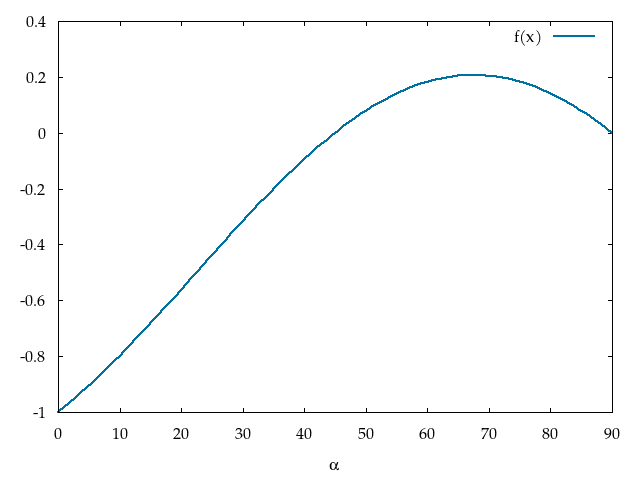
Z grafu vidíme, že funkcia nadobúda maximum pri \(\alpha=\ang{67.5}\), a že pri \(\ang{45}\) a menších uhloch je nemožné doskočiť na okraj. Minimálna energia na jeden skok je \[ E = \frac{mgh}{4}\frac{1}{\sin(\ang{67.5})\cos(\ang{67.5}) - \cos^{2}(\ang{67.5})}. \]

Ako môžeme vidieť, energia závisí jedine od výšky, a to lineárne. Takže na dva skoky o jeden schod blcha spotrebuje rovnako veľa energie ako na jeden skok o dva schody. Teda ani jeden spôsob skákania nie je výhodnejší, než ten druhý.

Je jedno akým spôsobom blcha skáče, takže na vyskákanie celého schodiska musí spraviť napríklad 12 skokov o jeden schod. Celková energia teda bude \[ E_{c} = \frac{3mgh}{\sin(\ang{67.5})\cos(\ang{67.5}) - \cos^{2}(\ang{67.5})}. \]