4. Vedecké strasti vzorové riešenie

Zadanie

Maťo opäť prežíva nervy drásajúce životné obdobie. Ďalší z jeho pokusov o zostrojenie perpetua mobile, od ktorého si toho toľko sľuboval, opäť skončil neúspechom. Jeho posledný model sa skladal z dvoch nádob spojených kapilárou, tak, ako je to znázornené na obrázku. Vodu nalial do nižšie položenej nádoby a dúfal, že začne stúpať kapilárou nahor, až dosiahne jej druhý koniec a odtiaľ bude odkvapkávať do druhej. Žiaľ, fyzikálne zákony boli proti. Maťo je s rozumom v koncoch a nevie, kde mohla nastať chyba. Vysvetlite, prečo jeho perpetuum mobile nefunguje.

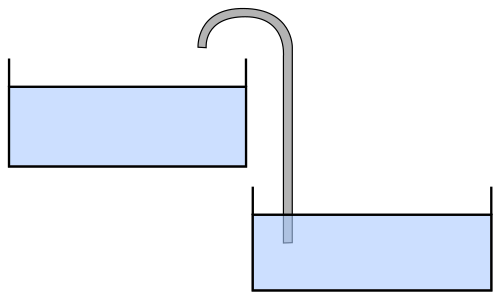
Predpokladajte, že výškový rozdiel nie je priveľký, t. j. kapilárny tlak zvládne vytiahnuť kvapalinu do potrebnej výšky.

Prv než sa pustíme do riešenia, zodpovedzme si najskôr na otázku, čo je to to perpetuum mobile. Wikipédia nám dáva nasledovnú odpoveď:¹

Perpetuum mobile je:

• hypotetické zariadenie, ktoré by trvalo vykonávalo prácu bez dodávania energie (perpetuum mobile prvého druhu);
• hypotetický periodicky pracujúci stroj, ktorý by všetko teplo odobraté zo zdroja premieňal na prácu (perpetuum mobile druhého druhu). Hneď nám je jasné, že nás bude zaujímať perpetuum mobile prvého druhu. Maťovmu zariadeniu totiž nemusíme dodávať žiadnu energiu a podľa jeho predstáv by mala voda pretekať do vyššie položenej nádoby, t. j. jej potenciálna energia by mala rásť.

Rozoberme si Maťove zariadenie na drobné. Vieme identifikovať štyri hlavné body, v ktorých by mohol nastať problém:

1. vzlínanie vody kapilárou;
2. pretečenie vody zakrivenou časťou kapiláry;
3. prúdenie vody kapilárou nadol;
4. odkvapkávanie vody z kapiláry. Postupne sa pozrieme na jednotlivé body a pokúsime sa identifikovať problém.

Začnime so vzlínaním. Hneď na úvod si vyjasnime, že atmosférický tlak nezohráva žiadnu úlohu, pretože rovnaký tlak je na hladine vody v nádobe i v kapiláre. Toto samozrejme bude platiť, aj keď voda v kapiláre bude v jej zakrivenej časti, resp. až za ňou, takže neskôr sa už k tomuto vracať nebudeme. Zostáva teda jediná možnosť – povrchové napätie. V škole nás naučili, čo je to povrchové napätie, takže sa tu nebudeme zaoberať fundamentálnymi poznatkami. Poznamenajme len, že existujú minimálne tri jednoduché prístupy, ako vysvetliť vzlínanie, ktoré si v krátkosti predstavíme.

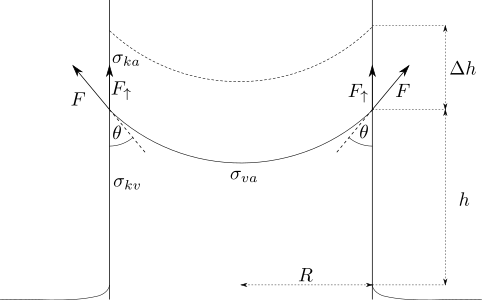
Asi najštandardnejší prístup je pomocou síl. Na kontakte kapiláry, vody a vzduchu spôsobuje povrchové napätie silu veľkosti \(F\) pôsobiacu v dotyčnicovom smere ku kvapaline, ktorá „vyťahuje vodu do kapiláry“.² Vertikálna zložka tejto sily má veľkosť \(F_{\uparrow}=F\cos\theta\), kde \(\theta\) je styčný uhol. Voda bude v kapiláre stúpať dovtedy, kým sa tiaž vodného stĺpca v kapiláre nevyrovná sile \(F_{\uparrow}\).

Druhý prístup³ využíva skutočnosť, že pod zakrivenou kvapalinou vzniká dodatočný kapilárny tlak. Tento dodatočný tlak spôsobí, že na hladinu vody v kapiláre bude pôsobiť tlaková sila nahor, a tá vyvolá vzlínanie. Popritom ale bude rásť hydrostatický tlak, ktorý sa prejaví tlakovou silou pôsobiacou na hladinu nadol. Vzlínanie sa ukončí, keď bude výsledná tlaková sila nulová, teda keď sa bude kapilárny tlak rovnať hydrostatickému.

Nás však bude najviac zaujímať tretí prístup, pretože ten využíva priamo energiu, no a energia je to, čo nás pri perpetuu mobile zaujíma. Vieme, že povrchová energia rozhrania dvoch prostredí je úmerná ploche tohto rozhrania. Koeficientom úmernosti je práve povrchové napätie daného rozhrania – matematicky vyjadrené \(E_{\mathrm{pov}}=\sigma S\).

Tu si musíme uvedomiť, že nielen rozhranie voda-vzduch (budeme označovať va) má nejaké povrchové napätie, ale rovnako i rozhrania kapilára-voda (kv) a kapilára-vzduch (ka) majú svoje povrchové napätia. Pre ďalšie úvahy budeme potrebovať porovnanie povrchových napätí \(\sigma_{kv}\) a \(\sigma_{ka}\), preto urobme nasledovnú úvahu. Je všeobecne známe, že fyzikálna sústava sa snaží nadobudnúť taký stav, aby mala čo najmenšiu energiu. Dôsledkom toho je zakrivenie hladiny v kapiláre. Vidíme, že kapilára „sa radšej dotýka vody než vzduchu“, t. j. voda zmáča kapiláru. V kontexte s tým, čo sme práve povedali o energii, môžeme prehlásiť, že rozhranie kv má menšiu povrchovú energiu než rozhranie ka, teda \(\sigma_{kv}<\sigma_{ka}\).

Teraz sa môžeme vrátiť k tretiemu prístupu. Čo sa deje s jednotlivými energiami, keď kvapalina v kapiláre vystúpi o \(\Delta h\)? V prvom rade si uvedomme, že je to z energetického hľadiska rovnaká situácia, ako keby sme z voľnej hladiny v nádobe zobrali trochu vody a položili ju na vrch vodného stĺpca v kapiláre. Musíme ju vyzdvihnúť do výšky \(h\),⁴ Teda i potenciálna energia sa zvýši o \[\mathop{\Delta E_{\mathrm{pot}}} = \mathop{\Delta m}gh = \pi r^{2}\rho gh \mathop{\Delta h}\text{,}\] kde \(r\) je polomer kapiláry. Zároveň sa však na úseku kapiláry o dĺžke \(\Delta h\) zmení typ rozhrania z ka na kv, teda povrchová energia sa zmení o \[\Delta E_{\mathrm{pov}} = \sigma_{kv} S-\sigma_{ka}S = \left(\sigma_{kv}-\sigma_{ka}\right)2\pi r\mathop{\Delta h} < 0\text{,}\] keďže \(\sigma_{kv}<\sigma_{ka}\).

Na úvod sme sa zhodli, že Maťo navrhuje perpetuum mobile prvého druhu, teda také, ktorému netreba dodávať žiadnu energiu. To znamená, že možno uvažovať jednoducho zákon zachovania energie. Odtiaľ už nie je problém dopočítať, do akej maximálnej výšky vie voda vystúpať. To nás však teraz nezaujíma. Pre nás je dôležité len to, pomocou akého mechanizmu vie do tejto medznej výšky vystúpať. No a to sme už zodpovedali. Voda môže zvyšovať svoju potenciálnu energiu na úkor toho, že klesá celková povrchová energia systému.

Tým sme uzavreli bod 1 a môžeme ísť ďalej. Tu už budeme podstatne stručnejší. Pokiaľ uvažujeme, že kapilára v mieste zahnutia je stále dostatočne tenká a zahnutie nie je veľmi ostré, voda bude stále upnutá i na horný okraj kapiláry, a teda kvalitatívne⁵ možno použiť rovnakú úvahu, čiže voda bude ďalej „cestovať“ kapilárou aj cez ohyb na úkor zníženia povrchovej energie. Nič sa nemení ani v prípade zostupu vody dolu kapilárou za ohybom.

Zostáva nám už len bod 4. Čo sa stane, keď voda dosiahne dolný koniec kapiláry? Okamžite vidíme, že náš model tu už prestáva fungovať, pretože ďalší postup nadol by si vyžadoval zväčšenie rozhrania kv na úkor ka. To už ale nie je kam rozšíriť. Navyše hneď na úvod sme si vyjasnili, že atmosférický tlak nezohráva žiadnu úlohu. Existuje ešte nejaká sila, ktorá by mohla donútiť vodu odkvapnúť z kapiláry? Snáď len gravitácia nám núka pomocnú ruku, lenže aj tú môžeme rýchlo zavrhnúť. Stačí si uvedomiť, že voda je prakticky nestlačiteľná, preto sa v kapiláre správa ako také homogénne lanko prehodené cez kladku, a to sa nikdy nebude pohybovať v smere kratšieho konca. Ak ešte chvíľu zostaneme v tejto analógii, môžeme sa pýtať, prečo sa teda nepohybuje v smere dlhšieho konca. No pretože za kratší koniec ťahá sila od povrchového napätia, ktorá ho drží v rovnováhe.

Maťov model teda zlyhal v jeho záverečnej fáze. Nie je možné, aby v prípade takto postaveného zariadenia voda odkvapkávala z kapiláry. Všimnime si ale, že v opačnom smere takéto zariadenie na prečerpávanie vody fungovať bude. V tomto prípade si totiž môžeme dovoliť predĺžiť otvorený koniec kapiláry pod úroveň toho ponoreného v hornej nádobe, takže odkvapkávanie bude možné (viď analógia s lankom). Samozrejme, že takto ale žiadnu energiu nezískame, naopak, časť strácame pri dopade kvapiek do dolnej nádoby, teda o perpetuu mobile v tomto prípade nemôže byť ani reči.

Poznámka o odkvapkávaní

Keď sme povedali, že voda z kapiláry nebude odkvapkávať, mysleli sme tým trvalé odkvapkávanie. Ukážeme si, že je teoreticky možné, aby pár kvapiek predsa len odkvaplo.

Vychádzali sme z energetickej bilancie. Povedali sme, že voda vystúpi do takej výšky, že pokles povrchovej energie je rovný nárastu potenciálnej energie. My však máme kapiláru presne určenej dĺžky. To znamená, že je presne daný pokles povrchovej a nárast potenciálnej energie, keď voda dosiahne horný koniec kapiláry.

Pre jednoduchosť uvažujme rovnú kapiláru dĺžky \(H\). Zaveďme funkciu \[\delta E\left(r\right)=-\left(\Delta E_{\mathrm{pov}}+\Delta E_{\mathrm{pot}}\right)=\left[2\left(\sigma_{ka}-\sigma_{kv}\right)-\frac{1}{2}r\rho gH\right]\pi rH\text{,}\] ktorá udáva energiu získanú pri vystúpení vody až po horný koniec rovnej kapiláry. Vidíme, že táto energia závisí okrem iného aj na jej polomere.

Vieme zvoliť taký polomer \(r_{0}\), aby voda vystúpila práve po horný koniec, teda \(\delta E\left(r_{0}\right)=0\). Uvažujme teraz kapiláru s polomerom \(r<r_{0}\). V takom prípade \(\delta E\left(r\right)>0\), teda nejakú energiu získame. Čo je to za energia?

V našich doterajších úvahách sme uvažovali statickú počiatočnú i konečnú situáciu. Neuvažovali sme pritom, že voda v kapiláre aj prúdi, teda má nejakú kinetickú energiu. Na záver však už žiadnu kinetickú energiu nemá. Kde sa teda stratila?

Vráťme sa naspäť k ohnutej kapiláre. Úvaha o kinetickej energii kvalitatívne platí aj v tomto prípade. Náš model elevácie samozrejme zostáva v platnosti, no musíme modifikovať záverečnú fázu. Predpokladajme, že voda dosiahne horný koniec kapiláry, no stále má nejakú kinetickú energiu. Čo sa teda bude diať? Voda bude pokračovať v pohybe. V prípade, že je kapilára dostatočne tenká, teda voda v nej stúpa dostatočne rýchlo, začne voda z horného konca kapiláry predsa len vystupovať.⁶

Začne sa tam formovať kvapôčka. Tým ale rastie povrch kvapaliny, a teda aj povrchová energia. V dôsledku toho bude kinetická energia vody v kapiláre klesať a vzlínanie vody bude ustávať. Ak kvapôčka dosiahne dostatočnú veľkosť, odkvapne. Takto môže odkvapnúť aj niekoľko kvapôčok, kým voda v kapiláre úplne nezastane. Dôležité však je, že táto prechodná fáza trvá len obmedzenú dobu a v konečnom čase skončí. Nijako pritom neporušuje zákon zachovania energie.