Zadanie
Maťovi sa stala na poslednom sústredku nepríjemná vec. Nalieval si mlieko. Keď usúdil, že má dosť, začal krabicu nakláňať do vertikálnej polohy. Mlieko sa v tom okamihu začalo rytmicky vylievať a pooblievalo celý stôl. To by ešte vôbec nebolo to najhoršie… však ho utrie!
Lenže mlieko zatieklo medzi dve sklenené podložky1 vzdialené od seba \(h = \SI{5}{\micro\metre}\) (sklo je pomerne hladké), vytvoriac tak kruhový fľak medzi sklenenými podložkami s polomerom \(R = \SI{20}{\centi\metre}\). Každá podložka váži \(m = \SI{1}{\kilo\gram}\).
Maťo sa rozhodol, že zdvihne hornú podložku a utrie rozliate mlieko medzi podložkami, no v dôsledku povrchového napätia to išlo akosi ťažko… Akú silu potrebuje Maťo na to, aby od seba oddelil dve sklenené dosky? A akú prácu pri tom vykoná?
Chýbajúce potrebné údaje si odmerajte, nájdite na internete alebo ich, ako správni fyzici, odhadnite :-).
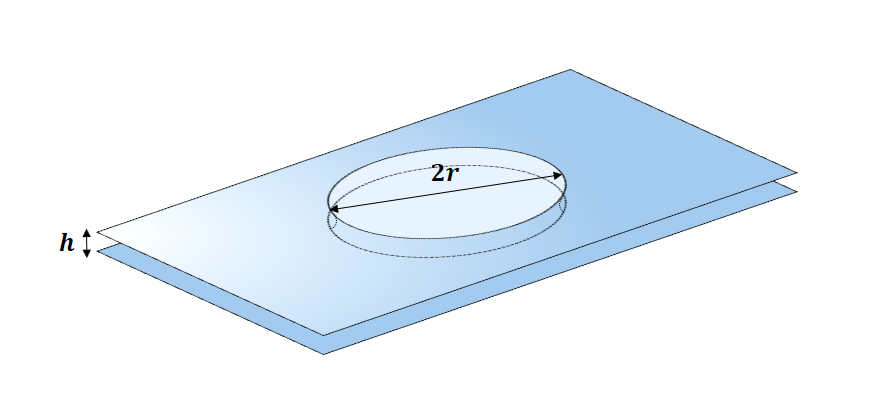
Pani kuchárky sa zjavne v školách v prírode extrémne snažia, aby sa drahým stolom nič nestalo, takže umiestnili na stôl rovno dve sklenené podložky namiesto jednej.↩︎
Riešenie tejto úlohy si rozdelíme na dve časti. Najprv sa pokúsime nájsť silu, ktorou musíme dosky od seba oddeľovať, ako funkciu vzdialenosti \(h\) medzi nimi. Ak sa nám to podarí, skúsime následne odhadnúť aj prácu, ktorú musíme vykonať na to, aby sme dosky od seba úplne oddelili. Tí z Vás, ktorí všetky tieto veci už zvládli, môžu rovno preskočiť väčšinu vzoráku a prečítať si niečo z okienka pre drtičov. Pustime sa do riešenia!
Akou silou musíme pôsobiť?
Ukážeme si dva spôsoby výpočtu. Oba sú niečím poučné. Na začiatok však spomenieme, že rovno zanedbáme tiažovú silu pôsobiacu na mlieko, keďže očakávame, že bude rádovo menšia ako sily povrchového napätia. Kto neverí, nech si odhadne túto silu, a potom ju porovná s výsledkom ;)
Spôsob prvý: Výpočet cez sily a tlaky
Nakreslime si kruhový fľak z profilu. Asi tušíme, že to bude vyzerať nejako takto:
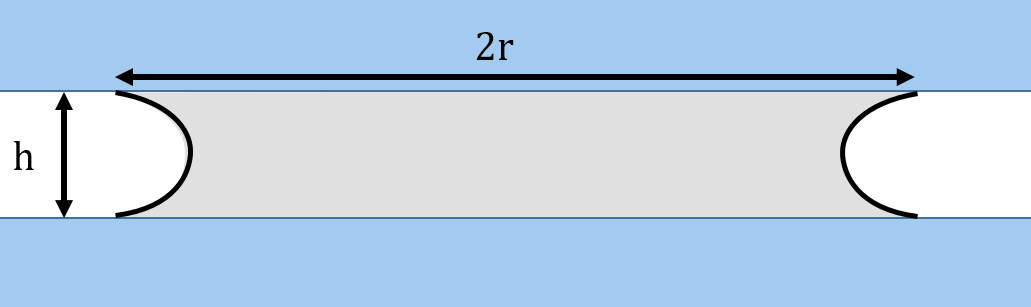
Ako však presne vyzerá tvar rozhrania medzi mliekom a vzduchom pri pohľade zboku? Je to časť kružnice? No, nie tak úplne. Pre \(h << R\) si však pohodlne vystačíme s tým, že to časť kružnice je. Keďže vo fyzike častokrát hľadáme iba približný výsledok, avšak stále zachytávajúci podstatné javy, s takýmto priblížením si bohato vystačíme1. Zvedavosť záujemcov, ktorí by chceli vedieť viac, bude uspokojená na konci tohoto vzoráku.
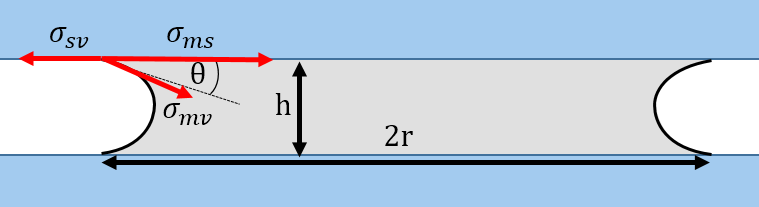
Na rozhraní mlieka, sklenenej podložky, a vzduchu pôsobia sily povrchového napätia v smere pozdĺžnom s príslušným rozhraním. Ak označíme povrchové napätie medzi mliekom a vzduchom \(\gamma_{\mathrm{mv}}\), mliekom a sklom ako \(\gamma_{\mathrm{ms}}\) a medzi sklom a vzduchom \(\gamma_{\mathrm{sv}}\), tak na rozhraní musí platiť rovnováha síl, z ktorej dostaneme vzťah \(\gamma_{\mathrm{mv}}\cos(\theta) + \gamma_{\mathrm{ms}} - \gamma_{\mathrm{sv}} = 0\)2, kde \(\theta\) je kontaktný uhol vyznačený na obrázku.
Keďže si chceme veci čo najviac zjednodušiť, urobíme horný odhad – povieme, že mliečko dokonale zmáča sklo, t. j. že \(\theta = 0\). Ďalej predpokladajme, že povrchové napätie medzi sklom a vzduchom je väčšie ako medzi sklom a mliekom3. Odteraz teda budeme pracovať iba s jednou hodnotou povrchového napätia \(\gamma = \gamma_{\mathrm{mv}}\).
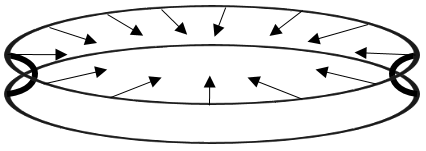
Pri pohľade zhora vytvára mlieko kruhový fľak s polomerom \(R\). Na rozhraní medzi mliekom a vzduchom na povrchu skla tak pôsobí celková sila \[F = \gamma \cdot 2\pi R\text{.}\]
Keďže máme dve podložky, sú dve aj rozhrania, a preto je celková sila rovná \(2 \cdot \gamma \cdot 2\pi R\). Povedali sme, že mlieko dokonale zmáča povrch skla, takže táto sila sa snaží mlieko rozliať po povrchu, t. j. pri pohľade zhora sa snaží zväčšiť kruhový fľak. Tlak v kvapaline je teda menší ako atmosférický, čo zase vytvára silu, ktorú musíme prekonať, ak chceme podložky od seba oddeliť.
Spomeňme si na základnú školu, kde nás učili o Pascalovom zákone. Ten hovorí, že ak na voľný povrch kvapaliny pôsobíme silou, vo všetkých miestach kvapaliny vzniká rovnaký tlak. Ak chceme zistiť hodnotu tohoto tlaku, musíme vypočítať plochu rozhrania medzi mliekom a vzduchom. Táto plocha je v princípe časť plášťa torusu. Fuj! Drtiči to majú povinne za domácu úlohu4, my ostatní si vystačíme s tým, že si povieme, že táto plocha nebude (rádovo) väčšia ako plocha plášťa valca s príslušnými rozmermi.
Odtiaľ získame hodnotu rozdielu tlakov medzi vnútrom mlieka a okolím5, \[ \Delta p = - \frac{\gamma 4\pi R}{2\pi R h} = -\frac{2\gamma}{h}\text{.} \]
Tento tlak je rovnaký vo všetkých miestach kvapaliny, a teda sklenená podložka je pritláčaná k druhej podložke silou \[ F= \pi R^2 \cdot \Delta p = \pi R^2 \frac{2\gamma}{h}\,\text{.}\]
Predtým, než si ukážeme druhý spôsob, si rovno skúsme vypočítať, aká veľká táto sila je. Hodnota povrchového napätia pre mlieko je \(\gamma \approx \SI{50}{\milli\newton\per\meter}\).6 Po dosadení hodnôt zo zadania sa dopracujeme k hodnote \[F \approx \SI{2400}{\newton}\text{.}\]
Čo je teda poriadna sila! Vidíme, že tiaž dosky a aj samotného mlieka je zanedbateľná. No je to daň za to, že pani kuchárky zjavne sklenené podložky dobre vyleštili :)
Uff. Bolo toho celkom dosť, no poďme ďalej a ukážme si druhý spôsob výpočtu.
Spôsob druhý: Metóda virtuálnych prác
Metóda virtuálnych prác nie je práve vec, ktorá by sa učila na strednej škole, no napriek tomu to nie je nič ťažké, čo by ste nezvládli už aj Vy. Je založená na tom, že sa pozrieme na situáciu v stave statickej rovnováhy. Potom si predstavíme, že sa súčasti systému posunú o nejaké maličké \(\Delta x\) a spočítame všetky možné práce, ktoré boli na systéme vykonané rôznymi (aktívnymi) silami. Princíp virtuálnych prác potom hovorí, že ak bol systém predtým v rovnováhe, všetky tieto práce rôznych síl musia dať v súčte nulu. Prečo niečo takéto funguje, sa dozviete buď na vysokej škole, alebo na sústredku. O tejto metóde môžete nájsť niečo viac tu7. Najlepšie tento princíp pochopíte na príklade, a preto si pomocou neho túto úlohu rovno vyriešime.
Pre jednoduchosť budeme mlieko medzi podložkami modelovať ako valec. Predstavme si, že pôsobíme silou \(F\) na hornú podložku, čím ju posunieme o \(\Delta h\). Potom vykonáme prácu \(F\Delta h\). Zároveň narastie aj výška valca o \(\Delta h\). Keďže je valec vyšší, tak plocha plášťa narastie o \(2\pi R\Delta h\). Plocha plášťa valca definuje plochu rozhrania medzi mliekom a vzduchom, a teda ovplyvňuje aj energiu povrchového napätia. Takže vieme, že zmena povrchovej energie je \(\gamma \cdot 2\pi R\Delta h\).
Položením týchto dvoch energií do rovnosti dospejeme k sile \(F = \gamma 2\pi R\). Vidíme, že výsledok je iný ako v predchádzajúcom prípade. Kde nastala chyba? Zabudli sme totiž na to, že objem mlieka medzi podložkami musí zostať konštantný, čo sa prejaví tak, že sa polomer podstavy valca musí zmenšiť o nejaké \(\Delta R\). Tento polomer prichádza do hry na rozhraní mlieko–sklo, ktoré má plochu \(2 \cdot \pi R^2\).
Objem mlieka sa musí zachovať, preto \(2\pi (R+\Delta r)(h+\Delta h) = 2\pi Rh\). Odtiaľ zanedbaním členu s \(\Delta r\Delta h\) získame \(\Delta r \approx -R\frac{\Delta h}{h}\). Rozdiel plôch rozhrania je medzikružie, teda zmena povrchovej energie na tomto rozhraní bude \(\gamma \cdot \pi{(R+\Delta r)}^{2}-\pi R^2 \approx \gamma 2\pi R\Delta R = -\gamma 2\pi R^2\frac{\Delta h}{h}\).
Položením všetkých príspevkov do rovnosti, \[ F\Delta h + \gamma \cdot 2\pi R\Delta h -\gamma 2\pi R^2\frac{\Delta h}{h} = 0\text{,} \]
získame hodnotu \[ F = \gamma\left(2\pi R + \pi R^2 \frac{2}{h}\right) \approx \pi R^2 \frac{2\gamma}{h}\text{,} \] kde sme zanedbali prvý člen, lebo \(R/h \gg 1\).8
Akú prácu vykonáme?
Už vieme, že sila závisí nepriamo úmerne od vzdialenosti \(h\) medzi doskami. Poďme odhadnúť prácu.
Jeden spôsob je urobiť horný odhad, a to nasledovne. Vieme, že sila závisí nepriamo úmerne od \(h\), zoberme teda veľkosť tejto sily na začiatku a vynásobme ju nejakou rozumnou vzdialenosťou \(\Delta h\), o ktorú musíme posunúť sklenenú podložku. Za rozumnú vzdialenosť možno napríklad považovať výšku vrstvy mlieka v prípade, že by bolo rozliate iba na jednej podložke. Táto vrstva bude mať najviac niekoľko milimetrov, preto \(\Delta h \approx \SI{1}{\milli\metre}\) (horný odhad)9.
Prvý odhad teda máme, \[ W \approx F(h)\Delta h = \SI{2.4}{\joule}\text{.} \]
Ak chceme niečo presnejšie, môžeme postupovať nasledovne. Uvedomíme si, že sila sa mení podľa vzdialenosti, a teda sčítame veľa malých príspevkov typu \(F(x)\Delta x\). Keď je \(\Delta x\) „nekonečne malé“, dostávame integrál. Ďalej výšku vrstvy, keď je mlieko rozliate iba na jednej podložke, vieme zistiť z minimalizácie energie (potenciálna + povrchová)10. Z minimalizácie energie vieme odhadnúť výšku vrstvy ako \(2\sqrt{\frac{\gamma}{\rho g}} \approx \SI{1.4}{\milli\metre}\). Intuícia nebola mimo.
O niečo lepší odhad teda získame ako \[ W = \int_h^{h+\Delta h} F(x)dx = 2\pi R^2\gamma \ln\left(1+\frac{\Delta h}{h}\right) \approx \SI{0.07}{\joule}\text{.} \]
Čo je o dosť menej! V skutočnosti to môže byť aj o kúsok viac, pretože ak budeme podložku dvíhať pomaly, je dosť možné, že sa nám podarí mliečko vytiahnuť aj do väčšej výšky ako tej, pri ktorej bude existovať po tom, ako sa sklenená podložka od neho oddelí. Centimetre to však asi nebudú, a keďže táto výška vystupuje pod logaritmom, výsledok sa zmení len o máličko.
Napokon si ešte spomenňme na to, že aj podložka niečo váži. Pri posune sklenenej podložky vážiacej \(m=\SI{1}{\kilo\gram}\) o \(\SI{1}{\milli\metre}\) vykonáme ešte navyše prácu \[ W_g = mgh \approx \SI{0.01}{\joule}\text{,} \] čo je približne sedemkrát menej ako práca, ktorú vykonáme kvôli povrchovému napätiu. Ďalším poučením je, že práca je síce relatívne malá, ale sklenené podložky sa nám ani tak tak ľahko nepodarí oddeliť.
Okienko pre drtičov a zopár poznámok
Tí z Vás, ktorých zaujalo povrchové napätie, si môžu pozrieť prednášku o tejto téme z Akadémie Trojstenu11. Tí z Vás, ktorí majú celý tento príklad už v malíčku, si môžu pozrieť niečo o Youngovi a Laplacovi12. Tvar mliečka medzi doskami, bude pri zanedbaní jeho tiaže katenoida13 s dodatočnou podmienkou na fixovaný objem (polomer fľaku a vzdialenosť medzi doskami spolu súvisia). S ňou ste sa mohli stretnúť aj v FX – pohľadajte v archíve. Takéto veci, ako sme riešili v tomto príklade, sa volajú capillary bridge.
Ak sa takýmto postupom aj k niečomu dopočítame a nebude to úplne odveci, môžeme povedať, že naše priblíženie nebolo od veci.↩︎
Táto rovnováha síl v princípe definuje kontaktný uhol.↩︎
Ak by sme ho aj uvažovali, len by to zmenilo efektívnu hodnotu \(\gamma\), s ktorou počítame ďalej, no nie princíp výpočtu.↩︎
Dá sa to aj bez integrálov. Návod: https://en.wikipedia.org/wiki/Pappus%27s_centroid_theorem↩︎
Záporné znamienko je za to, že tlak v mliečku je menší ako atmosférický tlak okolo.↩︎
Ak použijeme hodnotu pre vodu (\(\SI{72}{\milli\newton\per\metre}\)), nedopustíme sa veľkej chyby. Spomínaná hodnota pochádza z A. J. Bertsch, Surface tension of whole and skim-milk between and ; Journal of Dairy Research (1983), 50, 259-26↩︎
Tento člen by vystupoval aj vo výsledku získanom prvým spôsobom, ale tam sme ho na jednom mieste potichu zanedbali. Skúste zistiť kde ;)↩︎
Postupujeme metódou fyzikálnej intuície. Autor vzoráku si nevie predstaviť, že by mu rozliate mlieko na stole vytvorilo centimetrovú vrstvu, prípadne väčšiu :)↩︎
Tí z Vás, ktorí nevedia ako na to, pozrite si v archíve príklad 6 – Mláčka z 1. kola zimnej časti 27. ročníka FKS.↩︎
https://en.wikipedia.org/wiki/Young%E2%80%93Laplace_equation↩︎
V angličtine catenoid↩︎
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.