2. Ľadovcová sánkovačka vzorové riešenie

Zadanie

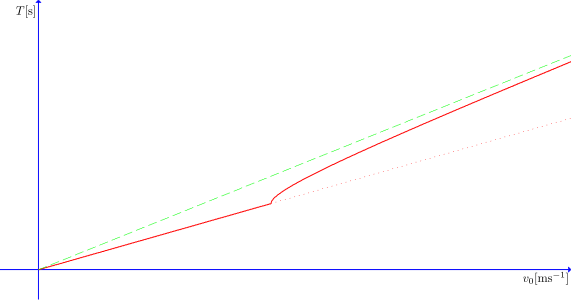
Filip sa počas svojho posledného alpského dobrodružstva rozhodol zdolať jeden z ľadovcov. A ten bol poriadne klzký, doslova nekonečne. Jeho súčiniteľ šmykového trenia bol totiž nulový, takže naň nebolo možné vyliezť. Keď už ho nedokázal zdolať, rozhodol sa ho aspoň zmerať. Zobral si kvádrik a udelil mu rýchlosť \(v_0\) nahor proti smeru spádnice ľadovca, pričom si zaznamenával čas \(T\), za ktorý sa vráti. Dáta, ktoré takto získal, sú vykreslené na obrázku. Na základe nich odhadnite, ako vyzerá profil ľadovca.

Úloha sa na prvý pohľad síce zdá byť náročná, no my sa jej nezľakneme a s vervou sa do nej pustíme. Veď profil ľadovca môže byť rôznorodý a jeho sklon sa teda môže všakovako meniť, čo znamená, že sa bude meniť aj zložka tiažového zrýchlenia, ktorá spôsobuje spomaľovanie, resp. zrýchľovanie kvádrika. Začnime preto s najjednoduchším modelom, a tým je naklonená rovina. Našou motiváciou môže byť napríklad skutočnosť, že akýkoľvek zložitý profil vieme vyskladať z veľkého počtu maličkých naklonených roviniek s rôznym sklonom.

Uvažujme naklonenú rovinu, ktorá zviera s horizontálnym smerom uhol \(\alpha\). Potom zložka tiažového zrýchlenia v smere spádnice naklonenej roviny má veľkosť \(a=g\sin\alpha\). Filipov kvádrik sa teda bude pohybovať s takýmto zrýchlením. Lenže to zostáva konštantné počas celého pohybu, keďže sa sklon roviny nemení, takže budeme vyšetrovať rovnomerne zrýchlený/spomalený pohyb.

Predpokladajme, že Filip udelil kvádriku rýchlosť \(v_{0}\). Potom je rýchlosť kvádrika v čase \(t\) popísaná notoricky známou rovnicou \(v\left(t\right)=v_{0}-at\). Vieme, že ľadovec je dokonale klzký, takže ak zanedbávame odpor vzduchu, potom pri kĺzaní kvádrika nedochádza k stratám energie, dôsledkom čoho je veľkosť vektora rýchlosti kvádrika pri návrate rovná jeho počiatočnej rýchlosti. Smer rýchlosti je samozrejme opačný.

Označme dobu pohybu kvádrika \(T\). Podľa predošlej úvahy je jeho rýchlosť v tomto čase \(v\left(T\right)=-v_{0}\), takže po dosadení do rovnice pre rovnomerne spomalený pohyb dostávame \(-v_{0}=v_{0}-aT\). Odtiaľ \[ T(v_0)=\frac{2v_{0}}{a}=\frac{2v_{0}}{g\sin\alpha}\text{.} \]

Dosiahli sme mimoriadne dôležitý poznatok, a to, že pre rovinný povrch ľadovca je čas do návratu kvádrika lineárnou funkciou jeho počiatočnej rýchlosti. Keď sa však pozrieme na Filipov graf, vidíme, že úsek od počiatku až po zlom v grafe vykazuje presne takúto závislosť. To môže znamenať len jediné – sklon ľadovca v jeho dolnej časti je konštantný.

Sklon grafu je určený konštantou úmernosti \(k=\frac{2}{g\sin\alpha}\), ktorá zodpovedá tangensu uhla medzi grafom a \(x\)-ovou osou. Ako vidíme, tá bezprostredne súvisí so sklonom ľadovca. Ak z grafu určíme konštantu úmernosti, vieme vypočítať sklon ľadovca podľa vzťahu \(\sin\alpha=\frac{2}{gk}\), resp. \(\alpha=\arcsin\left(\frac{2}{gk}\right)\). Okamžite vidíme, že čím je sklon grafu väčší, tým je sklon ľadovca menší. To dáva zmysel, pretože vyšší sklon grafu hovorí, že kvádriku trvá dlhšie, než zastane a vráti sa späť. To naozaj zodpovedá prípadu, keď je zrýchlenie menšie, a tým pádom je nižší aj sklon ľadovca.

Teraz sa zamyslime, čím by mohol byť spôsobený zlom v grafe. Po krátkej kontemplácii si uvedomíme, že do úvahy pripadajú dve, či tri možnosti:

• mení sa sklon ľadovca;
• v ľadovci je priehlbina, teda na istom úseku ľadovca jeho sklon klesá, no a potom znova stúpa;
• časť povrchu ľadovca má horizontálny smer;
• alebo kombinácia prvej s niektorou z ďalších možností.

Aby sme vedeli rozhodnúť, ktorá z týchto troch možností zodpovedá realite, zamyslime sa nad tým, ako by sa každá z nich prejavila na grafe. Začnime s druhou. Názorný príklad je načrtnutý na obrázku.

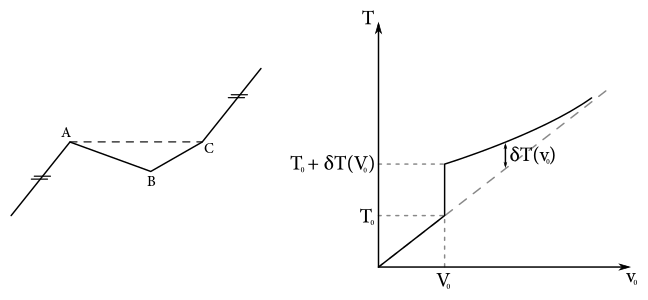
Uvažujme najprv prípad, že kvádrik má takú počiatočnú rýchlosť \(V_{0}\), aby zastal tesne pred bodom A a skĺzol sa späť. To nech mu trvá čas \(T_{0}\). Teraz uvažujme, že má o máličko vyššiu počiatočnú rýchlosť, takú, že sa cez vrchol A prepadne do priehlbiny. Tu najskôr zrýchľuje, až dosiahne dno B, a potom začne spomaľovať, až v bode C zastane a skĺzne sa cez priehlbinu späť až k Filipovi. Prekonanie priehlbiny ho oproti predchádzajúcemu prípadu bude v súčte oboch prechodov stáť oneskorenie \(\delta T\). Ak teraz uvážime prípad, že kvádrik bude mať v bode A nenulovú rýchlosť, tak po prekonaní priehlbiny zastane až nad bodom C a skĺzne sa späť. Tentokrát ale prekoná priehlbinu vyššou rýchlosťou, teda nadobudnuté oneskorenie bude oproti predošlému prípadu nižšie.

Vidíme teda, že oneskorenie je závislé na rýchlosti, ktorou sa kvádrik cez priehlbinu pohybuje, a teda de facto na počiatočnej rýchlosti \(\delta T\left(v_{0}\right)\). Čím je počiatočná rýchlosť vyššia, tým je vyššia rýchlosť pohybu cez priehlbinu, a teda oneskorenie je nižšie. Ak je rýchlosť v priehlbine dostatočne vysoká, čas strávený v priehlbine je zanedbateľne malý v porovnaní s časom, ktorý strávi kvádrik mimo nej, čo sa na grafe prejaví tak, že sa asymptoticky približuje k priamke popisujúcej pohyb kvádrika, ako keby tam žiadna priehlbina nebola. Pre nás je podstatné, že žiaden takýto skok vo Filipovom grafe nevidíme, takže na ľadovci žiadna priehlbina byť nemôže.¹

Prv, než začneme analyzovať vplyv zmeny sklonu ľadovca na tvar grafu, pristavme sa ešte v krátkosti pri možnosti existencie horizontálneho úseku ľadovca. Bez sebemenších výpočtov môžeme túto teóriu zavrhnúť. Stačí, že si uvedomíme, že je to len limitný prípad predchádzajúceho prípadu pre depresiu s nulovou hĺbkou. Čím je depresia plytšia, tým pomalšie v nej kvádrik zrýchľuje a spomaľuje, a teda mu prechod cez ňu trvá dlhšie, teda pre tento prípad by sme dostali v grafe ešte väčší skok.

No a teraz už šup-šup na prípad zmeny sklonu ľadovca. Keď sa pozornejšie pozrieme na Filipov graf, všimneme si, že pre vysoké počiatočné rýchlosti sa asymptoticky blíži k priamke s väčším sklonom, než má priamka zodpovedajúca sklonu ľadovca v jeho dolnej časti. V súlade s tým, čo sme už skôr rozoberali, môžeme tvrdiť, že táto priamka zodpovedá ľadovcu s miernejším sklonom, než je sklon v dolnej časti. Ako rozumný tip sa teda javí, že v istom bode sa sklon ľadovca mení k miernejšiemu. To vysvetľuje asymptotické správanie grafu. Pre vysoké počiatočné rýchlosti totiž kvádrik strmšou spodnou časťou ľadovca len rýchlo preletí, takže tento úsek prispeje k celkovému času do návratu len málo, a teda sklon grafu je v takomto prípade určený predovšetkým hornou časťou ľadovca. Čím je počiatočná rýchlosť vyššia, tým je príspevok od spodnej časti zanedbateľnejší a o to viac sa graf približuje k priamke zodpovedajúcej hornej časti ľadovca.

Posledná vec, na ktorú treba nájsť odpoveď, je, ako sa mení sklon ľadovca. Ak by sa menil postupne, vedeli by sme ho po častiach aproximovať kratučkými úsečkami, ktorým by na \(v_{0}-T\) grafe zodpovedali priamky s blízkymi sklonmi. Prechodu medzi úsečkami by zodpovedal prechod medzi dvomi susednými priamkami. Čím by boli úsečky kratšie, tým by bol výsledný graf hladší. Postupnému prechodu medzi rôznymi sklonmi ľadovca teda zodpovedá hladký graf. Filipov graf však obsahuje hrot, takže sklon ľadovca sa musí meniť skokovo, resp. na ďaleko menšej škále, než sú rozmery rovinných častí ľadovca. Ľadovec môže teda vyzerať tak, ako je načrtnutý na obrázku.