4. Ťarcha presnosti vzorové riešenie

Vzorové riešenie tejto úlohy si rozdelíme na dve časti. V prvej si predstavíme metódy, aké sa dajú použiť a aj sa používali, resp. sa stále používajú na meranie tiažového zrýchlenia a prediskutujeme ich presnosť. V druhej časti si potom vyberieme niektorú z prezentovaných metód a vykonáme vlastné merania.

Na úvod venujme pár slov všeobecným informáciám o tiažovom zrýchlení Zeme a jeho meraní. Je to taká bohatá téma, že sa ňou zaoberá samostatný odbor geofyziky – gravimetria. Dnes vieme merať tiažové zrýchlenie s vysokou presnosťou. Napríklad Förste (2015) uvádza hodnotu \(g=\SI{9.807246731}{\metre\per\second\squared}\). Je zrejmé, že hodnota tiažového zrýchlenia variuje v priestore i v čase. Uveďme si na príklade tejto hodnoty, ktorý rád ovplyvňujú aké faktory (čísla odpovedajú cifrám):

• 0 – sploštenie Zeme a rotácia (odstredivá sila);
• 7 – začínajú sa prejavovať nehomogenity rozloženia hmoty Zeme; pohoria, oceánske chrbty, výškový rozdiel \(\SI{1}{\kilo\metre}\);
• 2 – nehomogenity hustoty vo vnútri Zeme;
• 4 – veľké vodné nádrže;
• 6 – začínajú sa prejavovať časovo premenné faktory; príliv a odliv, výškový rozdiel \(\SI{1}{\metre}\);
• 7 – obrovské budovy, podzemná voda;
• 3 – oceánska topografia (odchýlka hladiny od sféry \(\sim\SI{1}{\metre}\)), pohyb zemského pólu;
• 1 – výškový rozdiel \(\SI{1}{\milli\metre}\).

V gravimetrii sa často stretneme s jednotkou \(\SI{1}{Gal} = \SI{1}{\centi\metre\per\second\squared}\). Dnes vieme merať tiažové zrýchlenie s presnosťou až \(\sim\SI{0.1}{\micro Gal}\). Pre lepšiu predstavu, tohoto rádu je gravitačné zrýchlenie od listu papiera (A4, \(\SI{80}{\gram\per\metre\squared}\)) \(\SI{13.5}{\centi\metre}\) pod jeho ťažiskom.

Poďme teraz už k metódam merania tiažového zrýchlenia. Vo všeobecnosti sa rozlišujú dva druhy meraní – absolútne a relatívne. Pri absolútnych meraniach sa určuje priamo veľkosť tiažového zrýchlenia. Pri relatívnych meraniach sa určujú rozdiely v tiažovom zrýchlení v priestore či v čase. To znamená, že vždy musíme najskôr vykonať absolútne meranie a až potom môžeme používať relatívne merania. Uvedomme si, že tiažové zrýchlenie sa nedá merať priamo. Vždy musíme vykonať aspoň dve merania – zväčša meranie dĺžky a času. V praxi sa využívajú dve základné metódy absolútneho merania, a to merania vykonávané pomocou kyvadiel a merania založené na voľnom páde.

Metóda kyvadiel

Najjednoduchším modelom kyvadla je matematické kyvadlo. Je známe, že pre periódu malých kmitov matematického kyvadla platí vzťah \(T=2\pi\sqrt{\frac{l}{g}}\), odkiaľ dostávame vyjadrenie pre tiažové zrýchlenie \[ g=\frac{4\pi^{2}l}{T^{2}}\text{.} \] Vidíme, že naozaj potrebujeme vykonať dve merania, a to meranie dĺžky závesu kyvadla \(l\) a jeho periódy \(T\). Uvedený vzťah pre periódu platí len pre malú amplitúdu kmitov \(\Phi\ll1\). Ak táto podmienka nie je splnená, treba použiť lepšiu aproximáciu \(T=2\pi\sqrt{\frac{l}{g}}\left(1+\frac{1}{16}\Phi^{2}+\frac{11}{3072}\Phi^{4}+\dots\right)\).

Matematické kyvadlo je len teoretický model, ktorý v skutočnosti neexistuje. Ako vhodnú korekciu môžeme započítať moment zotrvačnosti závažia. V prípade závažia guľového tvaru (\(J_{0}=\frac{2}{5}mr^{2}\)) s použitím Steinerovej vety vieme nájsť modifikovaný vzťah pre periódu kmitov kyvadla \(T=2\pi\sqrt{\frac{l}{g}\left[1+\frac{2}{5}\left(\frac{r}{l}\right)^{2}\right]}\), kde \(r\) je polomer závažia. Ak \(r\to0\), naozaj dostávame vzťah pre matematické kyvadlo.

To sme sa už ale dostali ku konceptu fyzikálneho kyvadla. Pre periódu fyzikálneho kyvadla platí \(T=2\pi\sqrt{\frac{J}{mg\xi}}\), kde \(J\) je moment zotrvačnosti kyvadla okolo osi závesu a \(\xi\) je vzdialenosť závesu od ťažiska. Zavedením redukovanej dĺžky kyvadla \(l_{r}=\frac{J}{m\xi}\) dostávame pre periódu \(T=2\pi\sqrt{\frac{l_{r}}{g}}\), čo je formálne rovnaký vzťah ako pre matematické kyvadlo.

Problémom fyzikálneho kyvadla je, že pre kyvadlá komplikovanejších tvarov nevieme presne lokalizovať ťažisko a určiť moment zotrvačnosti. S týmto problémom sa vieme vysporiadať použitím metódy reverzného kyvadla. Táto metóda využíva skutočnosť, že na každej osi prechádzajúcej ťažiskom kyvadla existuje dvojica bodov A a B ležiacich na tej istej polosi od ťažiska, v ktorých keď kyvadlo zavesíme, bude kmitať s rovnakou periódou. Nech príslušné vzdialenosti bodov závesu od ťažiska sú \(\xi_{A}\) a \(\xi_{B}\). Jednoduchým výpočtom sa dá ukázať, že \(\xi_{A}+\xi_{B}=l_{r}\), čo je redukovaná dĺžka kyvadla vystupujúca vo vzťahu pre periódu, no a vzdialenosť závesov nie je problém merať, teda na výpočet tiažového zrýchlenia pomocou reverzného kyvadla možno použiť vzťah \[ g=\frac{4\pi^{2}l_{r}}{T^{2}}\text{.} \]

Reverzné kyvadlo je zvyčajne realizované dvojicou pohyblivých závaží umiestnených na opačných koncoch tyče, ktoré vieme po tejto tyči posúvať, čím efektívne meníme moment zotrvačnosti kyvadla, a tým aj jeho redukovanú dĺžku. Problémom býva nájsť dvojicu osí, pre ktoré má kyvadlo presne rovnakú periódu. Z toho dôvodu sa na výpočet \(g\) používajú merania okolo dvoch osí s blízkymi periódami \(T_{A,B}=2\pi\sqrt{\frac{J_{0}+m\xi_{A,B}^{2}}{mg\xi_{A,B}}}\). Vylúčením momentu zotrvačnosti okolo ťažiska \(J_{0}\) z rovníc dostávame vzťah pre tiažové zrýchlenie \[ g=4\pi^{2}\frac{\xi_{A}^{2}-\xi_{B}^{2}}{T_{A}^{2}\xi_{A}-T_{B}^{2}\xi_{B}}\text{.} \] V praxi sa polohy závaží na kyvadle volia tak, aby rozdiel \(\left|\xi_{A}-\xi_{B}\right|\) bol čo najväčší. Za tohto predpokladu možno zavedením priemernej periódy \(T_{p}=\frac{T_{A}+T_{B}}{2}\) odvodiť pre tiažové zrýchlenie vzťah \[ g\approx\frac{4\pi^{2}l_{r}}{T_{p}^{2}}\left(1-\frac{l_{r}}{T_{p}}\frac{T_{A}-T_{B}}{\xi_{A}-\xi_{B}}\right)\text{,} \] ktorý pre \(T_{A}=T_{B}\) prechádza na vyššie uvedený vzťah na výpočet tiažového zrýchlenia pri použití reverzného kyvadla.

Zaoberajme sa chvíľu presnosťou merania tiažového zrýchlenia použitím kyvadiel. Nepresnosť merania \(g\) vypočítame podľa vzťahu \[ \delta g = \sqrt{\left(\frac{\partial g}{\partial l_{r}}\delta l_{r}\right)^{2}+\left(\frac{\partial g}{\partial T}\delta T\right)^{2}} = g\sqrt{\left(\frac{\delta l_{r}}{l_{r}}\right)^{2}+4\left(\frac{\delta T}{T}\right)^{2}}=\frac{g}{l_{r}}\sqrt{\left(\delta l_{r}\right)^{2}+\frac{gl_{r}}{\pi^{2}}\left(\delta T\right)^{2}}\text{,} \]

kde \(\delta l_{r}\) je nepresnosť merania redukovanej dĺžky a \(\delta T\) je nepresnosť merania periódy. Pre \(l_{r}=\SI{1}{\metre}\) dostávame \(\delta g\approx10\left(\sqrt{\left(\delta l_{r}\right)^{2}+\left(\delta T\right)^{2}}\right)\).

Metóda reverzných kyvadiel sa používala na meranie tiažového zrýchlenia dlhé roky. V roku 1862 sa podarilo touto metódou zmerať tiažové zrýchlenie s presnosťou až \(\SI{3}{\milli Gal}\). Túto presnosť sa dlho nedarilo prekonať. Až v roku 1979 sa podarilo zmerať \(g\) touto metódou s presnosťou až \(\SI{0.3}{\milli Gal}\), čím sa narazilo na limity tejto metódy.

Metóda voľného pádu

Posledných asi 30 rokov sa na meranie tiažového zrýchlenia používa metóda založená na voľnom páde. Ak uvažujeme homogénne tiažové pole neznámej veľkosti \(g\), tak medzi dobou pádu \(t\) a dráhou pádu \(h\) platí vzťah \[ h = \frac{1}{2}gt^{2}\text{,} \]

odkiaľ nie je problém vyjadriť hľadané \(g\).

Pre naše potreby je táto metóda dostačujúca, v praxi však nie. Spomeňme si, čo sme povedali na začiatku. Dráha voľného pádu pri meraní sa pohybuje rádovo aspoň v metroch. Lenže pri takýchto výškových rozdieloch sa prejavujú zmeny tiažového zrýchlenia na úrovni \(\sim \SI{0.1}{\milli Gal}\), čo je hraničná presnosť pre metódu kyvadiel. To znamená, že metóda voľného pádu pri uvažovaní homogénneho tiažového poľa nie je presnejšia než metóda kyvadiel. Môžeme však predpokladať, že tiažové zrýchlenie sa v prvom priblížení mení s výškou lineárne, teda \(g\left(y\right)=g+\gamma y\). Napíšme si pohybovú rovnicu pre padajúce teleso v takomto prípade: \[ m\ddot{y}=mg+m\gamma y\text{.} \] Ak by sme ju vyriešili, tak pre výšku pádu dostaneme vzťah \[ h=\frac{g}{\gamma}\left[\cosh\left(\sqrt{\gamma}t\right)-1\right]\approx\frac{1}{2}gt^{2}\left(1+\frac{\gamma}{12}t^{2}+\dots\right)\text{.} \] Všimnime si, že v ňom vystupujú dve neznáme – \(g\) a \(\gamma\) – takže treba vykonať aspoň dve merania. V praxi sa však na spracovanie získaných dát častejšie používa metóda najmenších štvorcov s dvomi voľnými parametrami.

Na zaistenie dostatočnej presnosti sa experiment vykonáva vo vákuovej komore. Padajúci objekt je navyše umiestnený do malej škatuľky padajúcej spolu s ním a poháňanej motorom, aby sa zabezpečila rovnaká rýchlosť padania, čím sa eliminuje aj odpor zostatkového vzduchu v komore. Experiment sa opakuje mnohokrát (\(>\num{1000}\)) a vyhodnocuje sa štatisticky. Pomocou tejto metódy sa dá dosiahnuť presnosť až \(\sim \SI{1}{\micro Gal}\), čo je zhruba o dva rády vyššia presnosť než pri použití kyvadiel.

Relatívne merania

Druhým typom meraní sú relatívne merania. Vo všeobecnosti sú presnejšie než absolútne merania, no ich hlavnou výhodou oproti absolútnym je predovšetkým ich jednoduchšia realizácia. Ich princíp spočíva v tom, že sa jedna meraná veličina zafixuje a meria sa len druhá. Relatívne merania nám umožňujú merať zmeny tiažového poľa na danom mieste v čase, prípadne zriedkavejšie rozdiel v tiažovom zrýchlení medzi dvomi miestami. Relatívne merania sa dajú rozdeliť do troch kategórií podľa použitej metódy – merania využívajúce kyvadlá, merania pružinovými gravimetrami a merania supravodivým gravimetrom.

Princíp relatívnych meraní najlepšie pochopíme na príklade metódy kyvadiel. Už vieme, že tiažové zrýchlenie vypočítame z nameranej redukovanej dĺžky a periódy podľa vzťahu \(g=4\pi\frac{l_{r}}{T^{2}}\). Zafixujme redukovanú dĺžku kyvadla \(l_{r}\). To znamená, že ak sa na danom mieste zmení tiažové zrýchlenie, zmení sa perióda kyvadla, ktorú meriame. Zo zmien periódy možno dopočítať zmenu tiažového zrýchlenia \[ \Delta g\approx-2\frac{g}{T}\Delta T\text{.} \]

Typická perióda používaných kyvadiel je rádovo \(\sim\SI{1}{\second}\), takže presnosť tejto metódy je \(\delta g\approx20\cdot\delta T\), kde \(\delta T\) je presnosť merania času. Metóda kyvadiel sa postupne zdokonaľovala. V druhej polovici minulého storočia sa na korekciu chýb spôsobených namáhaním materiálu začali používať dva páry kyvadiel a presnosť sa zvýšila až na \(\num{0.2}\mathrm{mGal}\). Metóda kyvadiel sa používala zhruba do 70. rokov minulého storočia.

Gravimetre sú tradične konštruované na princípe pružín. Pružinové gravimetre možno rozdeliť na statické a astatické. Princíp statických gravimetrov je veľmi jednoduchý. Uvažujme závažie hmotnosti \(m\) na pružinke pokojovej dĺžky \(l_{0}\) s tuhosťou \(k\). V stave statickej rovnováhy platí pre dĺžku pružinky vzťah \(l=l_{0}+\frac{m}{k}g\). Ak sa na danom mieste zmení hodnota tiažového zrýchlenia, zmení sa dĺžka pružinky. Zo zmeny dĺžky pružinky možno dopočítať zmenu tiažového zrýchlenia podľa vzťahu \[ \Delta g\approx\frac{k}{m}\Delta l\text{.} \]

Tuhosť pružiny je problematické určiť s dostatočnou presnosťou. S využitím vzťahu pre periódu kmitov \(T=2\pi\sqrt{\frac{m}{k}}\) možno ale tuhosť zo vzťahu vylúčiť a dostaneme \[ \Delta g\approx\left(\frac{2\pi}{T}\right)^{2}\Delta l\text{.} \]

Zadefinujme citlivosť gravimetra ako jeho odozvu na zmenu tiažového zrýchlenia \[ e=\frac{\mathrm{d}l}{\mathrm{d}g}=\frac{1}{4\pi^{2}}T^{2}\text{.} \]

Úmernosť medzi citlivosťou gravimetra a štvorcom jeho vlastnej periódy je všeobecnou vlastnosťou všetkých pružinových gravimetrov. To znamená, že teoreticky môžeme merať zmeny tiažového zrýchlenia s ľubovoľnou presnosťou za predpokladu, že perióda vlastných kmitov gravimetra je dostatočne veľká. Príkladom pružinového gravimetra je Askania gravimeter.

Problémom statických gravimetrov je ich silná odozva na zmenu tiažového zrýchlenia. Inými slovami, keď gravimeter vychýlime z rovnovážnej polohy, vratná sila bude veľká a závažie gravimetra sa rozkmitá s vysokou frekvenciou. Z toho dôvodu sa gravimetre konštruujú dômyselne, aby sa tomuto javu predchádzalo – hovoríme o tzv. astatizácii a o astatických gravimetroch. Príkladom takéhoto gravimetra je LaCoste&Romberg gravimeter.

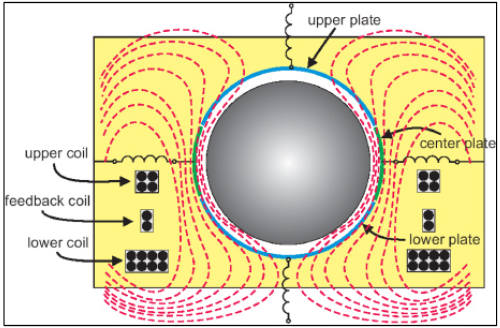
V súčasnosti najpresnejšie gravimetrické merania sú vykonávané pomocou supravodivého gravimetra. Ten pozostáva z cievok so spoločnou osou vo vertikálnom smere a gule zo supravodivého materiálu. Dve cievky zo supravodivého materiálu vytvárajú mierne nehomogénne, no časovo nemenné magnetické pole. Po zapnutí tohto poľa sa na povrchu supravodivej nióbovej gule podľa Faradayovho zákona indukujú prúdy, ktoré tečú po horizontálnych kružniciach. Magnetické pole je z gule vytláčané v súlade s Meisner-Ochsenfeldovým efektom.

Smer magnetického poľa od indukovaných prúdov je daný Lenzovým zákonom. Výsledkom toho je, že na guľu pôsobí magnetická sila smerom nahor, ktorá vyrovnáva tiažovú silu, takže guľa levituje. Ak sa zmení veľkosť tiažového poľa, guľa má tendenciu pohnúť sa. Tomu sa zabraňuje tým, že do “feedback cievok” sa púšťa časovo premenný prúd, ktorý mierne upravuje magnetické pole tak, aby magnetická sila na sféru presne reflektovala zmeny tiažovej sily, a tým sa zabezpečí to, že sféra zostáva v rovnováhe. Z prúdu tečúcim “feedback cievkou” sa určí zmena tiažového zrýchlenia. Magnetické pole cievok musí byť extrémne stabilné, preto je nutné dôsledne odtieniť vplyv magnetického poľa Zeme. Ak sa to urobí dobre, nepresnosť supravodivého gravimetra je \(\lesssim \SI{1}{\micro Gal}\).

Meranie

Teraz už máme všetky potrebné informácie, takže môžeme pristúpiť k meraniu. V prvom rade si vyberieme svoju obľúbenú metódu. Je zrejmé, že vyberať budeme z metód absolútneho merania. Naše možnosti sú teda dosť obmedzené. Pre potreby vzorového riešenia sme si vybrali metódu voľného pádu.

Z plastelíny sme si vyrobili guľôčku s polomerom \(r=\SI{2}{\centi\metre}\). Digitálne kuchynské váhy povedali, že mala hmotnosť \(m=\SI{60}{\gram}\). Nechali sme ju padať z výšky \(H=\SI{1.81}{\metre}\) a natáčali sme si to na video. Použitá kamera mala snímkovaciou frekvenciu \(f=\SI{24}{\hertz}\), čo znamená, že sme mali informáciu o polohe guľôčky každých \(\Delta t=\SI{0.041667}{\second}\).

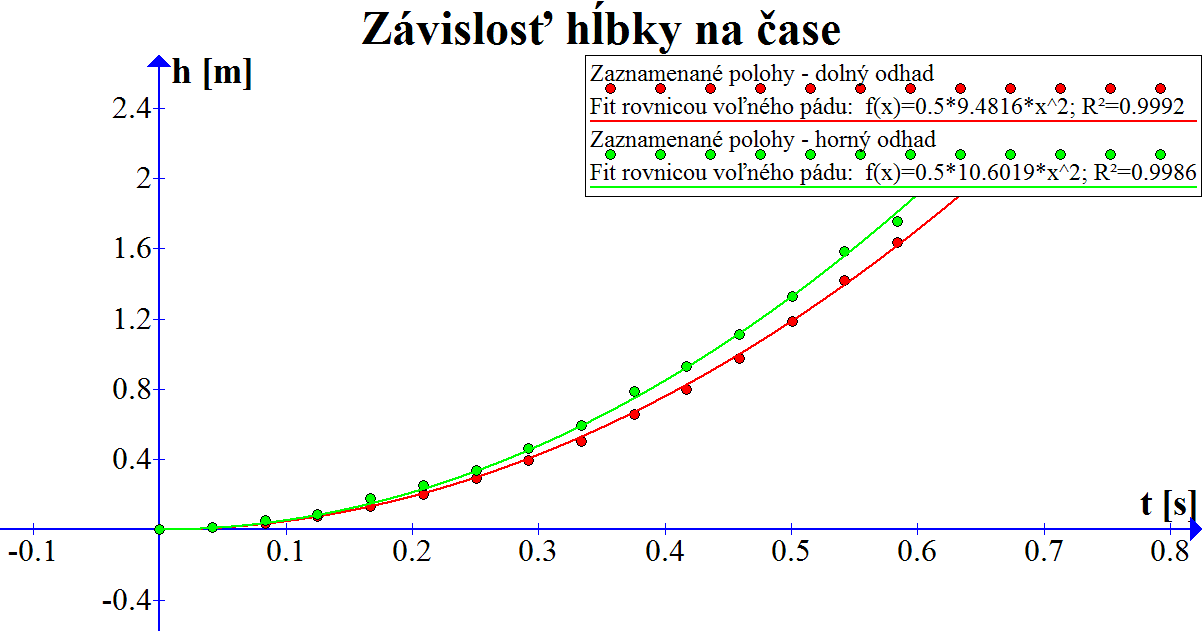
Po zrealizovaní experimentu už len zostávalo z videa odčítať hĺbku, do ktorej sa guľôčka dostala oproti počiatočnej polohe, v jednotlivých časových hladinách. Tu sa objavil obrovský problém – kamera obyčajného digitálneho fotoaparátu nedokázala zachytiť okamžitú polohu guľôčky, a tak keď tá dosiahla vyššie rýchlosti, na snímkach už nie je guľôčka ale pretiahnutý tieň obdĺžnikového tvaru. Toto je systematická chyba, ktorú nedokážeme odstrániť opakovaným meraním, takže nemalo zmysel opakovať meranie viackrát. Miesto toho sme z videozáznamu určili aspoň horný a dolný odhad, a to tak, že sme merali vždy prejdenú dráhu po horný i dolný koniec tieňa. Tým sme dostali dáta, na grafe zobrazené červenými a zelenými krúžkami pre dolný, resp. horný odhad.

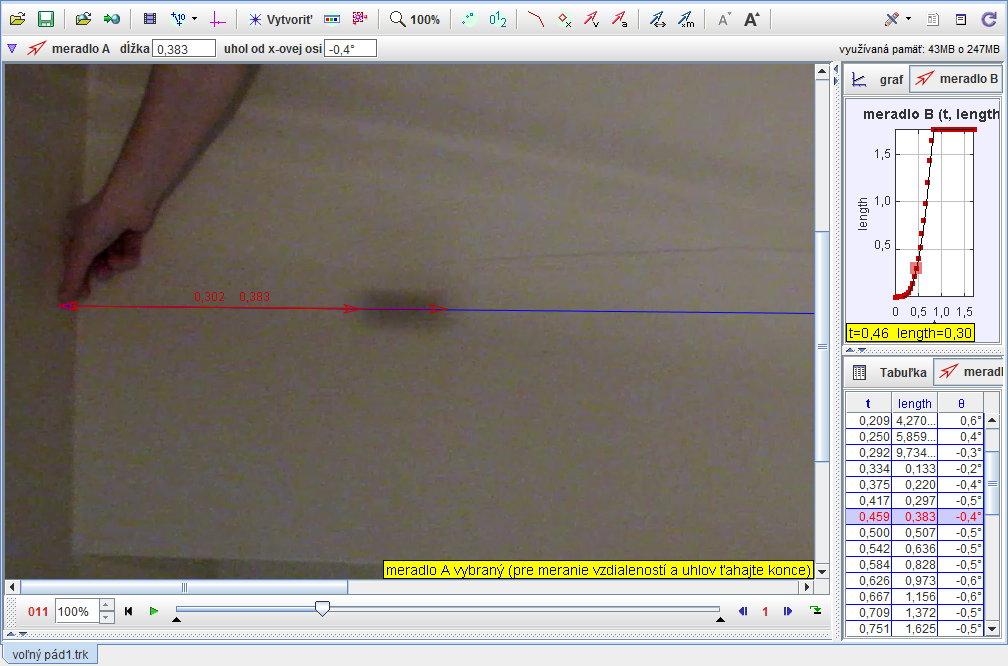
Na získanie tiažového zrýchlenia z nameraných dát sme použili metódu najmenších štvorcov. Pre hĺbku, do ktorej sa dostane guľôčka pri voľnom páde za čas \(t\), platí vzťah \[ h\left(t\right)=\frac{1}{2}gt^{2}\text{,} \] kde \(g\) je hľadané tiažové zrýchlenie. Ešte sa presvedčme o tom, že pád našej guľôčky môžeme považovať naozaj za voľný. Gravimetrické merania sa totiž vykonávajú vo vákuu. My sme však experiment vykonali za bežných atmosférických podmienok. Porovnajme teda rád tiažovej a odporovej sily. Guľôčka mala hmotnosť \(m=\SI{60}{\gram}\), takže na ňu pôsobila tiažová sila veľkosti \(F_{G}\approx\SI{0.6}{\newton}\). Pre odporovú silu pri turbulentnom obtekaní platí vzťah \(F_{o}=\frac{1}{2}CS\varrho v^{2}\), kde \(C\) je koeficient aerodynamického odporu (pre guľu \(C\approx\num{0.2}\)), \(S\) je čelný prierez gule (pre našu guľu s \(r=\SI{2}{\centi\metre}\), \(S\doteq\SI{12.6}{\centi\metre\squared}\)), \(\varrho\approx\SI{1}{\kilo\gram\per\metre\squared}\) je hustota vzduchu a \(v\) je rýchlosť, ktorú guľôčka dosiahla – pri trvaní pádu menej než \(\SI{0.6}{\second}\) je to menej než \(v=\SI{6}{\metre\per\second}\). Pre tieto hodnoty \(F_{o}\approx\SI{3.6e-3}{\newton}\), čiže \(\frac{F_{o}}{F_{G}}\approx\num{6e-3}\). Vidíme, že odporová sila je o viac než dva rády nižšia než tiažová, takže pád guľôčky možno naozaj považovať za voľný a namerané dáta teda možno fitovať funkciou v uvedenom tvare.

Povedzme si aspoň v krátkosti, na čom je založená metóda najmenších štvorcov.¹ Máme nameraný súbor dát \(\left[t_{i}; h_{i}\right]\). Dáta sme vyniesli do grafu a chceme ich preložiť takou krivkou, aby čo najlepšie zodpovedala nameraným dátam. V našom prípade vieme, že to má byť parabola \(h=\frac{1}{2}gt^{2}\). Chceme teda nájsť taký parameter \(g\), aby súčet štvorcov \(\sum_{i}\left(h_{i}-\frac{1}{2}gt_{i}^{2}\right)^{2}\) bol čo najmenší.

Výpočet prenecháme svojmu obľúbenému tabuľkovému kalkulátoru či inému programu na spracovanie dát. Pre nami získané dáta dostávame dolný odhad tiažového zrýchlenia \(g\doteq\SI{9.48}{\metre\per\second\squared}\) a horný odhad \(g\doteq\SI{10.6}{\metre\per\second\squared}\). V oboch prípadoch je koeficient determinácie vyšší než \(\num{0.99}\), takže namerané dáta naozaj zodpovedajú predpovedanej teoretickej závislosti.

My sme však ambiciózni a neuspokojíme sa s takýmto hrubým odhadom. Vyskúšajme, či metódou kyvadla nedosiahneme presnejšie výsledky. Rozhodneme sa, aký typ kyvadla na meranie použijeme. My sme si zvolili matematické kyvadlo. Z plastelínovej guľôčky z predchádzajúceho merania sme ho zostavili jednoducho. Predvídali sme, že budeme chcieť robiť aj toto meranie, preto sme pri jej výrobe do stredu vložili gombík s nitkou, ktorej koniec trčal z guľôčky, takže už stačilo len predĺžiť záves.

Dĺžka kyvadla od osi otáčania po stred guľôčky bola \(l=\SI{73.0\pm0.2}{\centi\metre}\gg r\), takže guľôčku možno považovať za hmotný bod. Kyvadlo sme zavesili a rozkývali. Opäť sme si celý priebeh natočili. Tentokrát sme natáčali na telefón, ktorého snímkovacia frekvencia bola \(f=\SI{30}{\hertz}\). To znamená, že sme odčítavali výchylky s časovým rozostupom \(\Delta t=\SI{0.0333}{s}\). Potom už len stačilo zvoliť si krátky úsek videa a snímku po snímke merať výchylku kyvadla.

Zo záznamu sme sa rozhodli odčítavať horizontálnu výchylku, nie uhol. Pre malé výchylky možno totiž kružnicový oblúk nahradiť dotyčnicou a vzdialenosť sa jednoduchšie meria než uhly. Získané dáta sú opäť zobrazené na grafe. Analyzovali sme len krátku sekvenciu videa, preto sa tlmenie nestihlo prejaviť a možno ho zanedbať. V takom prípade ale kyvadlo koná harmonické kmity a časová závislosť horizontálnej výchylky kyvadla je popísaná funkciou \[ x\left(t\right)=A\cos\left(\omega\cdot t\right)\text{,} \]

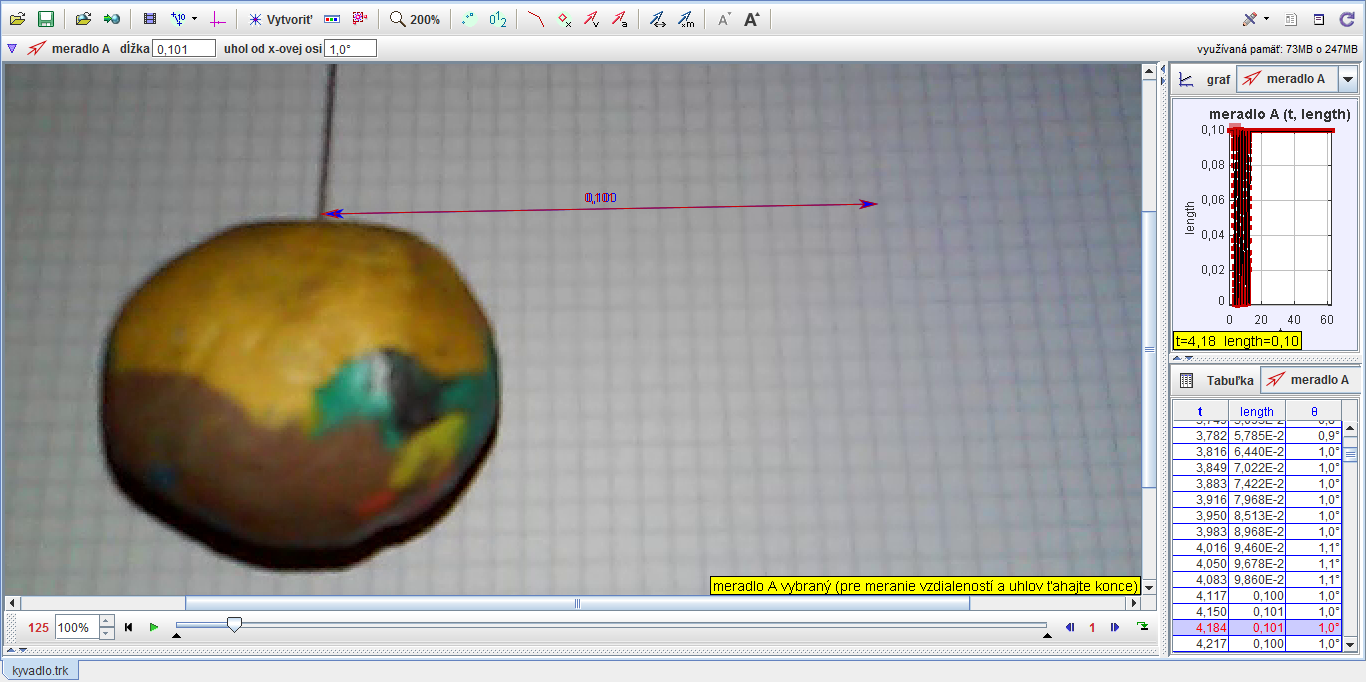
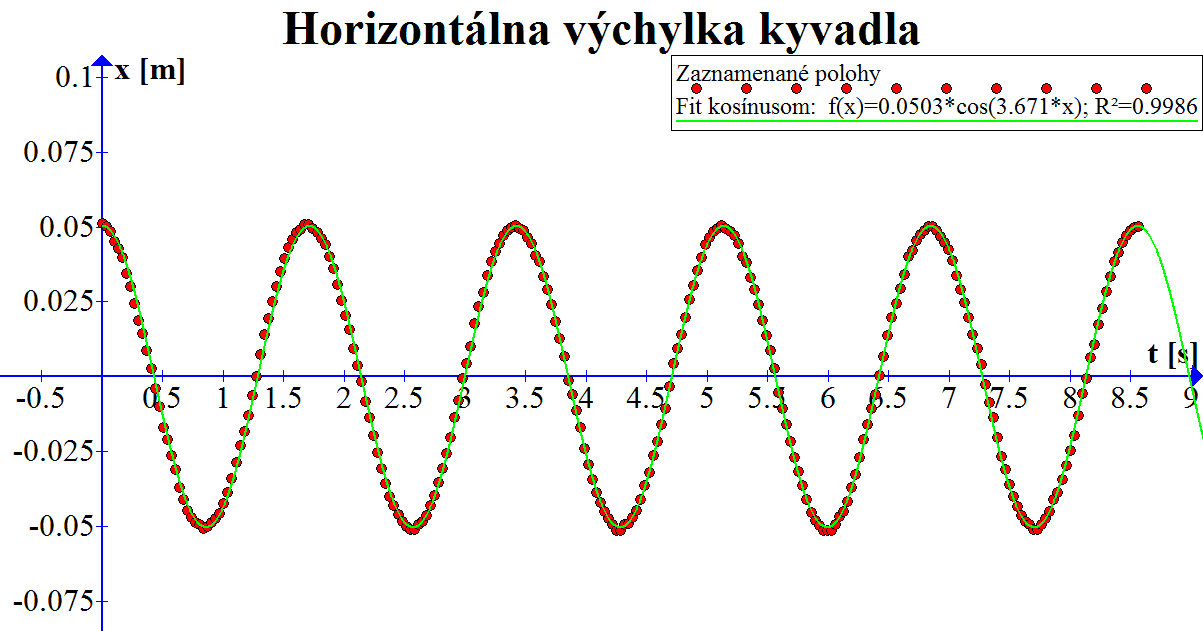
kde \(A\) je amplitúda kmitania a \(\omega\) uhlová frekvencia. Dáta sme opäť spracovali metódou najmenších štvorcov. Tentokrát voľnými parametrami boli práve amplitúda a uhlová frekvencia. Dopracovali sme sa k hodnotám \(A=\SI{5.03}{\centi\metre}\) a \(\omega=\SI{3.671}{\per\second}\). Koeficient determinácie je opäť vyše \(\num{0.99}\), takže matematický model dobre fituje namerané dáta. Ešte môžeme odhadnúť neistotu merania. Pre odhad smerodajnej odchýlky merania \(x\) dostávame \(\sigma_{x}=\SI{0.13}{\centi\metre}\). Odtiaľ možno odhadnúť smerodajnú odchýlku vlastnej frekvencie kyvadla ako \(\sigma_{\omega}\approx\frac{2\omega}{\pi A}\sigma_{x}=\SI{0.063}{\per\second}\).

Vieme, že vlastná frekvencia kmitania matematického kyvadla je daná vzťahom \(\omega=\sqrt{\frac{g}{l}}\). Vzhľadom na to, že \(l=\SI{73.0 \pm 0.2}{\centi\metre}\), môžeme jednoducho dopočítať hľadané tiažové zrýchlenie \[ g=\omega^{2}l=\SI{9.84}{\metre\per\second\squared}\text{.} \]

Podľa pravidiel o skladaní chýb dostávame \(\sigma_{g}=g\cdot\sqrt{\left(2\cdot\frac{\sigma_{\omega}}{\omega}\right)^{2}+\left(\frac{\sigma_{l}}{l}\right)^{2}}\approx\SI{0.34}{\metre\per\second\squared}\). Táto chyba je však veľmi nadhodnotená. V skutočnosti by sme mali uvažovať smerodajnú odchýlku priemeru definovanú ako \(\sigma_{\overline{x}}=\frac{\sigma_{x}}{\sqrt{N}}\), kde \(N\) je počet meraní. Keď vykonáme tie isté výpočty s touto novou hodnotou, dostaneme lepší odhad \(\sigma_{\overline{g}}\approx\SI{0.04}{\metre\per\second\squared}\). Aby sme dostali odhad krajnej chyby, treba túto hodnotu prenásobiť Studentovým koeficientom. Pre \(\SI{95}{\percent}\) mieru pravdepodobnosti je jeho hodnota približne \(\num{2}\), takže dostávame \[ g=\SI{9.84 \pm 0.08}{\metre\per\second\squared}\text{.} \]

Vykonali sme teda merania obomi prezentovanými spôsobmi. Metódou matematického kyvadla sme sa dopracovali k hodnote, ktorá je veľmi blízka skutočnej hodnote tiažového zrýchlenia. Metódou voľného pádu sme sa dopracovali len k veľmi hrubému odhadu tiažového zrýchlenia, ale to bolo dôsledkom nedostatočného technického vybavenia a nie dôsledkom presnosti metódy. V skutočnosti metóda založená na voľnom páde je presnejšia než metóda kyvadiel a v súčasnosti sa používa na kalibrovanie relatívnych gravimetrov.