4. Kovboj požiarnikom vzorové riešenie

Zadanie

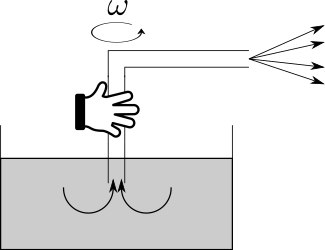
Dušan zistil, že aj obyčajná hadica sa dá použiť ako vodné čerpadlo. Ponorte jeden koniec do väčšej nádoby s vodou a začnite krútiť druhým koncom vo vzduchu, akoby ste mali laso. Budete pozorovať, že voda v hadici začne stúpať, prípadne až vystrekovať. Zmerajte závislosť výšky výstupu vody od obvodovej rýchlosti konca hadice. Prečo vlastne voda začala stúpať?

Teória

Máme systém voda + hadica + vzduch. Keď je tento systém statický, voda v hadici sa drží na úrovni hladiny vody. Zároveň je v hadici aj mimo nej atmosférický tlak.

V momente, keď začneme trubicou otáčať, dochádza k vzájomnému pohybu medzi voľným koncom hadice a okolitým vzduchom. Predstavme si, že sedíme na konci hadice, teda okolo nás prúdi vzduch rýchlosťou \(v\) (čiže pôvodné \(v = 0\) prešlo na \(v > 0\)). Podľa Bernoulliho rovnice zvýšenie rýchlosti spôsobí zníženie tlaku, takže vzniká podtlak:

\[\frac{1}{2} \rho_{\mathrm{vzduch}} v_1^2 + p_1 = \frac{1}{2} \rho_{\mathrm{vzduch}} v_2^2 + p_2\text{.}\]

V našom prípade je \(p_1\) tlak v trubici, keď ňou nehýbeme, \(v_1 = 0\) a \(v_2\) je obvodová rýchlosť.

Výsledkom je, že na jednom konci vzniká prúdenie vzduchu, a voda na druhom konci hadice je „vcucávaná“ do hadice. Úroveň hladiny vody v hadici stúpne. Úpravou Bernoulliho rovnice (pri položení \(v_1 = 0\)) vieme stanoviť rozdiel tlakov ako

\[\Delta p = \frac{1}{2} \rho_{\mathrm{vzduch}} v_2^2\text{.}\]

Zároveň z rovnice pre hydrostatiku poznáme vzťah \[\Delta p = \rho_{\mathrm{voda}} g h\text{.}\]

Z druhej a tretej rovnice vieme vyjadriť výšku \(h\), do ktorej voda vystúpa:

\[h = \frac{\rho_{\mathrm{vzduch}} v_{2}^2}{2 \rho_{\mathrm{voda}}g}\]

Z tohoto výrazu je pre nás dôležité, že výška výstupu hladiny vody v hadici je závislá kvadraticky od obvodovej rýchlosti, teda v grafe budeme očakávať parabolu.

Experiment

Pri tomto meraní bolo možné postupovať viacerými spôsobmi. Uvádzame merania troch riešiteľov – Mariána Poturnaya, Michaely Leinwatherovej a Mateja Hrma – ktoré nás zaujali pekným prevedením, či svojou originalitou. Výsledky ich meraní (grafy) uvádzame na konci.

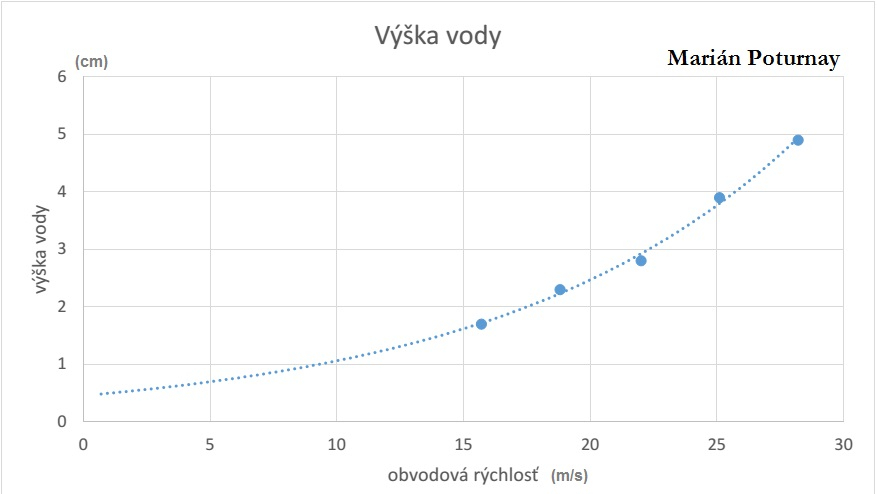
Marián Poturnay:

Počas experimentu som použil lavór plný vody, priehľadnú hadicu, telefón s kamerou, fixku a moje ružové Pikachu pravítko. Poprosil som brata, aby ma natáčal a ja som pritom zobral hadicu. Vždy som ju chytil za to isté miesto, aby polomer otáčania bol rovnaký (samozrejme som si ho odmeral: \(\SI{0.5}{\metre}\)). Potom som hadicu ponoril do vody tak, aby vždy bola pod vodou rovnaká časť (označené fixkou), a začal ňou krútiť. Voda vyšla do istej výšky. V mieste, kam až dosiahla voda, som chytil hadicu. Potom som ju vytiahol a odmeral výšku, do ktorej voda vystúpila. Následne som preštudoval videozáznam, z ktorého som zistil uhlovú rýchlosť otáčania hadice, z ktorej som vypočítal obvodovú rýchlosť.

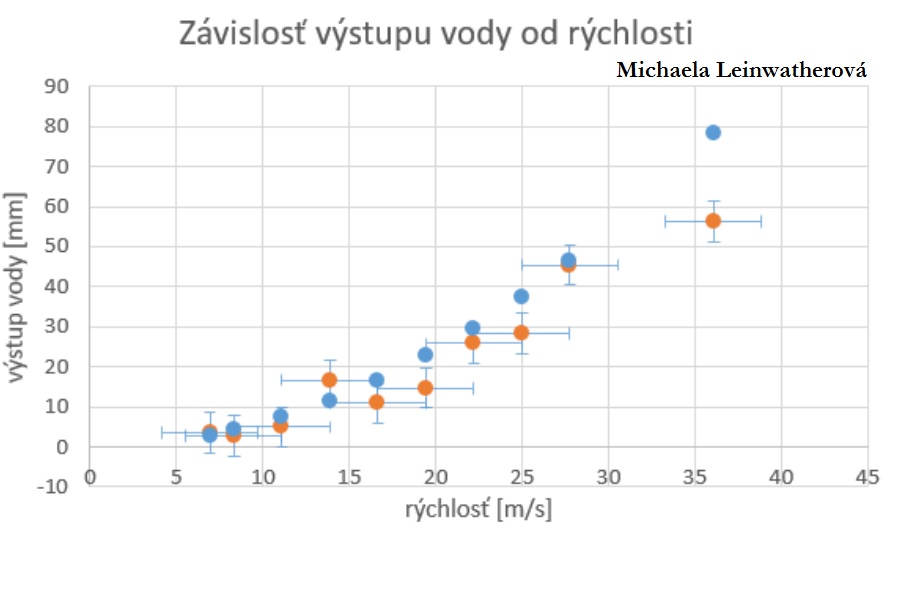
Michaela Leinwatherová:

Pre zvýšenie presnosti som sa rozhodla urobiť meranie v idúcom aute. Koniec hadice bol vystrčený z okna kolmo na smer jazdy. Hladinu vody v hadici som merala v závislosti od rýchlosti auta.

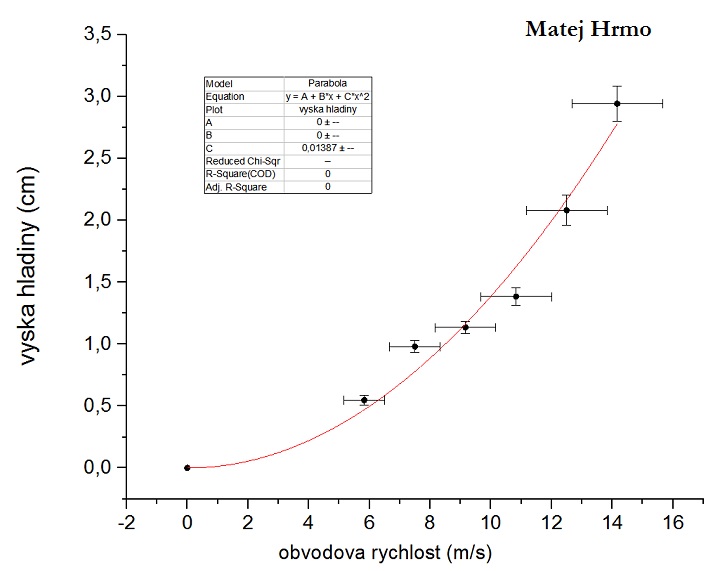
Matej Hrmo:

Zostavili sme si aparatúru z Lega, pričom sme použili motorček zo sady Technic. Pomocou jednoduchého prevodu (1:1) z ozubených koliesok sme zabezpečili otáčanie slamky ponorenej do vody. Gumenou hadičkou sme pripojili druhú slamku kolmo na prvú tak, aby sa mohla voľne otáčať vo vodorovnej rovine. Aby slamka nenarážala do konštrukcie a ostala v rovine, pridali sme malý kotúč z kartónu ako stabilizáciu.

Všetky tri uvedené merania boli úspešné, a teda na grafoch zobrazujúcich potrebnú závislosť môžeme vidieť kvadratický vyťah medzi obvodovou rýchlosťou a výškou výstupu hladiny.