5. Áno, trenie vzorové riešenie

Zadanie

Nina sa hrá s pružinkami. Minule zobrala dvojicu identických pružiniek s tuhosťou \(k\) a s nulovou pokojovou dĺžkou a pripevnila ich na protiľahlé steny kvádrika s hmotnosťou \(M\). Kvádrik potom položila na podložku a voľné konce pružiniek prichytila k dvojici pevných, protiľahlých stien. Následne kvádrik vychýlila z rovnovážnej polohy do vzdialenosti \(L\) a uvoľnila ho. Koľkokrát prejde kvádrik rovnovážnou polohou, než zastane? Koeficient trenia medzi kvádrikom a podložkou je \(f\).

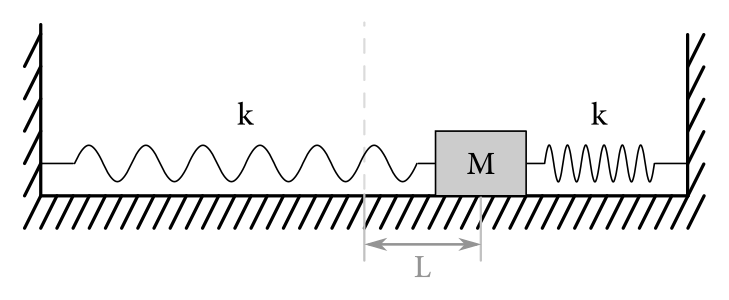
Zaveďme si súradnicovú sústavu tak, že \(x\) je vodorovná súradnica s počiatkom v rovnovážnej polohe závažia.

Uvažujme, že závažie je vychýlené do vzdialenosti \(x_{0}\). Nájdime, akou silou \(F_{p}\) pôsobia pružinky na závažie v tejto polohe. Predpokladajúc, že rovnovážna poloha závažia je od stien vzdialená \(D\), pružinky sú natiahnuté na dĺžky \(D\pm x_{0}\). Výsledná sila od pružiniek je teda \[ F_{p} = k\left(D + x_{0}\right) - k\left(D - x_{0}\right) = 2kx_{0}. \] Vidíme, že Ninina sústava pružiniek je ekvivalentná jedinej pružinke s tuhosťou \(K=2k\). Ďalej preto budeme počítať s takouto zástupnou pružinkou.

Vychýľme teda závažia do vzdialenosti \(x_{0}\) a preskúmajme dve po sebe idúce krajné polohy závažia. Nech po \(n\)-tom prechode rovnovážnou polohou je maximálna výchylka závažia \(x_{n}\) a po \(\left(n + 1\right)\)-om \(x_{n+1}\). Po \(n\)-tom prechode v krajnej polohe je celá mechanická energia sústavy uložená v potenciálnej energii pružinky \(E_{n} = \frac{1}{2}Kx_{n}^{2}\), po \(\left(n + 1\right)\)-om prechode \(E_{n + 1} = \frac{1}{2}Kx_{n+1}^{2}\). Straty energie sú spôsobené trením, preto rozdiel medzi týmito energiami je zrejme rovný práci trecej sily medzi polohami \(x_{n}\) a \(x_{n + 1}\). Veľkosť trecej sily je \(F_{t}=Mgf\) a pôsobila na dráhe \(\left|x_{n}\right|+\left|x_{n+1}\right|\), preto \[ \begin{aligned} E_{n} - E_{n+1} &= F_{t}\left(\left|x_{n}\right| + \left|x_{n+1}\right|\right) \\ \frac{1}{2}K\left|x_{n}\right|^{2}-\frac{1}{2}K\left|x_{n+1}\right|^{2} &= F_{t}\left(\left|x_{n}\right|+\left|x_{n+1}\right|\right) \\ \frac{1}{2}K\left(\left|x_{n}\right|-\left|x_{n+1}\right|\right) &= F_{t} \\ \left|x_{n+1}\right| &= \left|x_{n}\right|-\frac{2F_{t}}{K}. \end{aligned} \]

Zaveďme si označenie \(a_{n}\equiv\left|x_{n}\right|\), nech sa zbavíme absolútnych hodnôt. Pre amplitúdu výchylky po \(n\)-tom prechode rovnovážnou polohou dostávame jednoduchý rekurentný vzťah \[ a_{n}=a_{n-1}-\frac{2F_{t}}{K}. \] Skúsme ho opakovane do seba dosádzať a sledujme, čo dostaneme: \[ \begin{aligned} a_{n} &= a_{n-1} - \frac{2F_{t}}{K}= \\ &= a_{n-2} - 2\frac{2F_{t}}{K} = \ldots = \\ &= a_{n-m} - m\frac{2F_{t}}{K} = \ldots = \\ &= a_{0} - n\frac{2F_{t}}{K}. \end{aligned} \]

Nech závažie prekmitne rovnovážnou polohou práve \(N\)-krát. V takom prípade maximálna výchylka po \(N\)-tom prekmitnutí je \[ a_{N} = a_{0} - N\frac{2F_{t}}{K}. \]

Aby závažie neprekmitlo aj \(\left(N+1\right)\)-vý krát, zrejme musí byť potenciálna energia v krajnej polohe menšia než práca trecej sily z krajnej polohy do rovnovážnej polohy. Ak by bola čo i len o trošku väčšia, závažie by prekmitlo už \(\left(N+1\right)\)-vý krát, preto \[ \frac{1}{2}Kx_{N}^{2} \stackrel{!}{<} F_{t}\left|x_{N}\right|, \] odkiaľ \[ a_{N} \equiv \left|x_{N}\right| < \frac{2F_{t}}{K}. \] Zároveň vieme, že amplitúda je nezáporná. Dostávame teda podmienku \[ 0\leq a_{N}=a_{0}-N\frac{2F_{t}}{K}<\frac{2F_{t}}{K}. \]

Odtiaľ \[ \begin{gathered} a_{0} \geq N\frac{2 F_{t}}{K} > a_{0} - \frac{2F_{t}}{K} \\ \frac{K}{2F_{t}} a_{0} \geq N > \frac{K}{2F_{t}} a_{0} - 1 \\ N = \left\lfloor\frac{K}{2F_{t}} a_{0}\right\rfloor \end{gathered} \]

Po dosadení príslušných výrazov za \(K\) a \(F_{t}\) a uvážiac, že počiatočná amplitúda je \(a_{0}=L\), konečne dostávame¹ \[ N = \left\lfloor \frac{kL}{Mgf}\right\rfloor. \]