3. Polemika s tyčkou vzorové riešenie

Pozrime sa najprv na to, aké sily pôsobia na oba náboje. V miestnosti máme zadané homogénne elektrické pole (tj. pole rovnaké v každom jeho bode) s intenzitou \(E\). Toto pole bude preto na každý z nábojov pôsobiť po celú dobu konštantnou silou s veľkosťou \(F_e=QE\). Samozrejme, aj náboje samotné okolo seba vytvárajú nejaké elektrické pole, to sa ale prejaví iba ich vzájomným priťahovaním, ktoré bude vyrušené normálovou silou nehmotnej tyčky medzi nimi. Výslednou silou pôsobiacou na náboje bude teda jedine sila \(F_e\). Tá má smer vždy zhodný so smerom elektrickej intenzity \(\vec{E}\) a znamienko určené znamienkom daného náboja, teda pre kladný náboj \(\vec{F_{e_1}}=Q\vec{E}\) a pre záporný \(\vec{F_{e_2}}=-Q\vec{E}\). V prípade, keď je ešte tyčka rovnobežná so smerom \(\vec{E}\), pôsobia obe sily \(F_{e_1}\) aj \(F_{e_2}\) priamo proti nej, ale opačnými smermi. Navzájom sa teda vyrušia a výsledná sila je nulová - ide o rovnovážnu polohu. Keď ale Mözgáč tyčku pootočí o nejaký malý ale nenulový uhol \(\alpha_0\), dostane sa tak do polohy, kde na ňu už pôsobí nenulový moment sily. Sily \(F_{e_1}\) a \(F_{e_2}\) sa totiž v tomto prípade už nevynulujú celé, ale iba ich zložky rovnobežné s tyčkou. Zložky kolmé na tyčku ňou začnú otáčať v smere uhlu \(\alpha\).

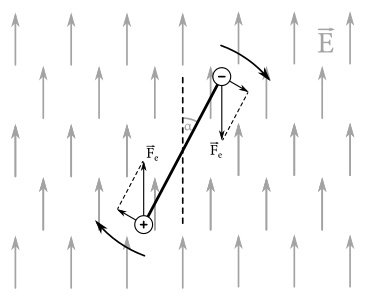
Obe kolmé zložky majú rovnakú veľkosť, a to \(F_e\sin\alpha\), takže os otáčania sa bude nachádzať presne v strede medzi nábojmi. Zároveň z toho vyplýva, že s rastúcim uhlom \(\alpha\) bude rásť aj moment sily, ktorý tyčku roztáča. To bude platiť, až kým \(\alpha\) neprekročí hodnotu \(\ang{90}\), kedy náboje dosiahnu svoje maximálne zrýchlenie. Odvtedy budú veľkosti kolmých zložiek \(F_{e_1}\) a \(F_{e_2}\) už iba klesať, až kým pre \(\alpha=\ang{180}\) nebudú opäť nulové. Tyčka sa tak dostane do stabilnej rovnovážnej polohy, v ktorej sú všetky výsledné sily nulové. Tak to ale nezostane nadlho. Keďže doteraz oba náboje neustále iba zrýchľovali, tyčka má zjavne v tomto momente svoju maximálnu uhlovú rýchlosť a bude sa preto otáčať aj ďalej. Po opustení rovnovážnej polohy začnú kolmé zložky síl \(F_{e_1}\) a \(F_{e_2}\) náboje naopak spomaľovať a pre uhol \(\alpha=\ang{270}\) budú pôsobiť maximálnym spomalením. Pohyb bude teda analogický k predchádzajúcej fáze pohybu, len bude akoby prebiehať odzadu. V prípade, že neuvažujeme žiadny odpor prostredia, sa tyčka zastaví až v momente, keď dosiahne stav ekvivalentný tomu počiatočnému. Takže ak Mözgáč tyčke na začiatku neudelil žiadnu uhlovú rýchlosť, zastaví sa na uhle \(\ang{360}-\alpha_0\). Ako ste si už isto uvedomili, ide o pohyb zhodný s pohybom matematického kyvadla a práve sme si popísali jeden jeho kyv. Keďže ale rozsah hodnôt výchylky \(\alpha\) nášho kyvadla je takmer \(\ang{360}\), nejde o štandardný lineárny oscilátor s malými výchylkami a harmonickým priebehom. To, že sila, ktorá vracia kyvadlo do rovnovážnej polohy (v našom prípade kolmá zložka \(F_e\)) nie je lineárne závislá od uhlu \(\alpha\) spôsobuje, že sa kyvadlo zdržiava dlhšie okolo hraničných hodnôt \(\alpha\) a kratšie v okolí rovnovážnej polohy. Ide teda o neharmonický kmitavý pohyb.

V druhej časti úlohy nás zaujíma hodnota maximálnej rýchlosti, ktorú náboje pri pohybe nadobudnú. Ako sme si už úvahou odvodili, pôjde o rýchlosť nábojov v rovnovážnej polohe, teda pre uhol \(\alpha=\ang{180}\). Keďže na túto rýchlosť boli náboje urýchľované iba silou (silami) \(F_e\) a uvažujeme, že sa mechanická energia sústavy zachováva, ich kinetická energia bude rovná práve práci sily \(F_e\). Teraz by sme si na určenie tejto práce mohli silu \(F_e\) rozkladať na zložku rovnobežnú s tyčkou a na zložku kolmú na tyčku a následne sčítavať príspevky tejto sily v smere trajektórie náboja, to ale vôbec nie je potrebné. Stačí si uvedomiť, že sila \(F_e\) je po celú dobu konštantná a prácu koná iba v smere rovnobežnom s ňou. V tomto smere prejde každý náboj iba dráhu \(L\), alebo ak chceme byť presní, tak dráhu \(\frac{L}{2}(1+\cos\alpha_0)\approx L\). Takže práca, ktorú vykoná sila \(F_e\) na jednom náboji bude \(W=QEL\). Z rovnosti tejto práce a kinetickej energie náboja dostávame hľadanú maximálnu rýchlosť nábojov. \[ \begin{aligned} 2 \cdot \frac{1}{2}mv^2 & = 2 \cdot QEL\\ v & = \sqrt{\frac{2QEL}{m}} \end{aligned} \]