5. Každý ročník treba valec! vzorové riešenie

Zadanie

Patrik si uvedomil, že trénovanie nových zručností je v móde. I vybral si aj on tú svoju – teleportáciu. Minule sa mu podarilo zobrať valec rotujúci okolo svojej osi uhlovou rýchlosťou \(\omega_0\), ktorý mal hmotnosť \(m\). Tento valec sa mu podarilo teleportovať na dlážku priamo k stene tak, ako vidíš na obrázku. Koľkokrát sa valec po teleportácii otočí okolo svojej osi, než úplne prestane rotovať? Medzi valcom a obomi stenami je koeficient trenia \(f\).

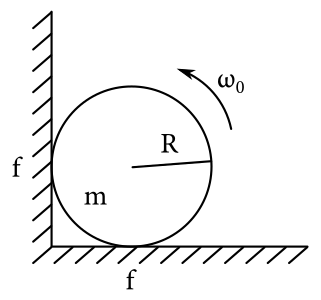
Ako to pri úlohách podobného typu chodí, na úvod si zostavíme rovnice pre sily a momenty síl. Treba si však dobre uvedomiť aké sily pôsobia a hlavne ktorým smerom.

Vo vertikálnom smere nám pôsobí trecia sila \(T_2\) od steny s pôsobiskom v bode dotyku a smerom, ktorý spomaľuje valec, teda smerom „hore“. Tiažová sila \(F_g\), ktorej pôsobisko bude v ťažisku valca so smerom „dole“ a nakoniec normálová sila \(N_1\) od podlahy s pôsobiskom v bode dotyku s podlahou a smerom hore.

V horizontálnom smere nám pôsobí normálová sila \(N_2\) od steny, s pôsobiskom v bode dotyku a so smerom „doprava“. Trecia sila \(T_1\) od podlahy s pôsobiskom v bode dotyku a smerom ktorý spomaľuje valec, teda „doľava“.

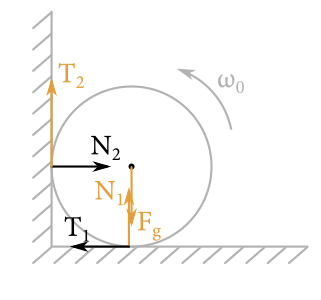
V poslednom kroku pred zostavením rovníc je dôležité si uvedomiť, ktoré sily budú mať vzhľadom na os rotácie valca moment. Sily \(F_g\), \(N_1\), \(N_2\) nemajú vzhľadom na os moment, takže v našej momentovej rovnici sa budú nachádzať jedine sily \(T_1\) a \(T_2\). Rovnako vieme, že rotácia valca sa postupne spomaľuje, preto je jeho moment \(I \epsilon\), kde \(I\) je moment zotrvačnosti a \(\epsilon\) uhlové zrýchlenie, resp. spomalenie.

Zostavme si teda rovnice: \[ \begin{aligned} T_2+N_1 &= F_g, \\ T_1 &= N_2, \\ I\epsilon &= -R \cdot \left(T_1 + T_2\right). \\ \end{aligned} \]

Vieme, že pre treciu silu platí \(T = f_N\), tiažová sila je \(F_g = mg\) a vzťah pre moment zotrvačnosti valca je \(I = \frac{1}{2}mR^2\). Preto naše rovnice napíšeme ako \[ \begin{aligned} fN_2+N_1 &= mg, \\ fN_1 &= N_2 \\ \frac{1}{2}mR^2\epsilon &= -Rf \cdot \left(N_1 + N_2\right). \\ \end{aligned} \]

Z druhej rovnice dosadíme \(N_2\) do prvej a vyjadríme si \(N_1\), \[ f^2 N_1 + N_1 = mg \quad\Rightarrow\quad N_1 = \frac{mg}{1 + f^2} \quad\Rightarrow\quad N_2 = \frac{fmg}{1 + f^2}. \]

Zistené \(N_1\) a \(N_2\) dosadíme do momentovej rovnice, no predtým v nej vykrátime jedno \(R\): \[ \begin{aligned} \frac{1}{2}mR\epsilon &= -f \cdot \left(\frac{mg}{1 + f^2} + \frac{fmg}{1 + f^2}\right), \\ \epsilon &= -\frac{2fg}{R} \cdot \frac{1 + f}{1 + f^2}. \\ \end{aligned} \]

Môžeme si všimnúť, že nám vyšlo uhlové zrýchlenie záporné, a teda sa jedná o spomalenie. Taktiež vidíme, že sme si ho vyjadrili cez všetky zadané parametre. Na to, aby sme zisitli počet otočiek, po ktorých valec zastane, potrebujeme si vyjadriť uhlovú rýchlosť v závislosti od času. Pre čas po ktorom valec zastane platí, že v ňom je rýchlosť nula, a preto \[ \Omega(t) = \omega_0-\left|\epsilon\right|t = 0 \quad\Rightarrow\quad t = \frac{\omega_0}{\left|\epsilon\right|}- \]

Pre uhol, o ktorý sa valec otočí, platí \[ \phi(t) = \omega_0 t - \frac{1}{2}\left|\epsilon\right|t^2 = \frac{\omega_0^2}{\left|\epsilon\right|} - \frac{1}{2}\left|\epsilon\right|\frac{\omega_0^2}{\left|\epsilon\right|^2} = \frac{1}{2}\frac{\omega_0^2}{\left|\epsilon\right|} \]

A teraz už máme vyhraté, pretože počet otočiek je vlastne iba opísaný uhol predelený uhlom jednej otáčky, čo je \(2\pi\): \[ N = \frac{\phi}{2\pi} = \frac{\omega_0^2}{4\pi\left|\epsilon\right|} = \frac{R\omega_0^2}{8fg\pi}\cdot\frac{1+f^2}{1+f}. \]

Počet otočiek, po ktorých valec zastane, je \(N = \frac{R\omega_0^2}{8fg\pi} \cdot \frac{1 + f^2}{1 + f}\).