7. Violet, indigo, blue, green, yellow, orange, red vzorové riešenie

Počas „cesty“ lúča sa stanú \(3\) zaujímavé veci: lom, odraz a zase lom. Tieto javy popisujú Zákon lomu a Zákon odrazu. Menej populárna časť z týchto zákonov hovorí, že zlomený či odrazený lúč ležia v rovine určenej dopadajúcim lúčom a kolmicou na povrch v mieste dopadu. Preto je táto úloha len dvojrozmerná, hoci vodná kvapka je trojrozmerná. Touto rovinou je rovina obsahujúca dopadajúci lúč a stred guľovej kvapky¹.

Všimnime si ešte jednu vec. Vyšlime z bodu, v ktorom nastal odraz, dva lúče. Jeden proti smeru dopadajúceho lúča a druhý v smere odrazeného lúča. Tieto dva lúče sú navzájom symetrické podľa priamky spájajúcej stred gule a bod, v ktorom sa lúč odrazí. Celá situácia tak musí byť symetrická podľa tejto priamky.

Teraz si už vieme nakresliť pekný obrázok toho, čo sa udeje:

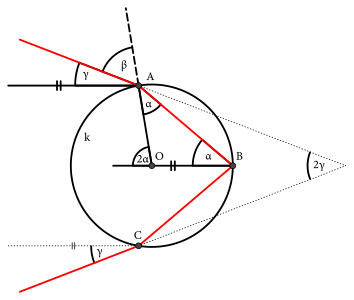
Už na obrázku sme si označili kružnicu, niekoľko bodov a niekoľko uhlov. Označili sme si:

• \(k\) kružnicu, ktorú vytne rovina, v ktorej sa nachádzajú lúče na povrchu kvapky,
• \(O\) stred guľovej kvapky²,
• \(A\) bod, kde nastal prvý lom,
• \(B\) bod, kde nastal odraz,
• \(C\) bod, kde nastal druhý lom,
• \(\alpha\) uhol \(ABO\),
• \(\beta\) uhol dopadajúceho lúča a priamky \(AO\),
• \(\gamma\) uhol dopadajúceho lúča a priamky \(BO\)³.

Nás bude najviac zaujímať ešte iný uhol – uhol dopadajúceho a vystupujúceho lúča. Ten vieme vyjadriť ako súčet dvoch uhlov. Uhla, ktorý zviera dopadajúci lúč s priamkou \(BO\), a uhla, ktorý zviera vystupujúci lúč s priamkou \(BO\). Pre prvý z týchto uhlov máme meno \(\gamma\) a druhý má zo symetrie podľa priamky \(BO\) tiež veľkosť \(\gamma\). Potrebujeme preto maximalizovať uhol \(2 \gamma\)⁴.

Hoci \(\gamma\) je ten uhol, ktorý potrebujeme nejako vyjadriť, máme o ňom málo informácií. O uhloch \(\alpha\) a \(\beta\) vieme toho povedať viac. Trojuholník \(OAB\) je totiž rovnoramenný, a teda aj uhol \(OAB\) má veľkosť \(\alpha\). Môžeme vidieť, že pri bode \(A\) je \(\beta\) uhol dopadajúceho lúča a \(\alpha\) uhol zlomeného lúča. Zo Snellovho zákona⁵ preto máme \[ \frac{\sin \beta}{\sin \alpha} = n. \qquad(1)\]

Tu \(n = \num{1.331}\) je relatívny index lomu na rozhraní voda-vzduch.

Stále však potrebujeme nejako vyjadriť \(\gamma\). Pozrime sa na uhly pri bode \(A\). Uhly \(\gamma\) a \(\beta\) spolu tvoria uhol medzi kolmicou dopadu a rovnobežkou s \(BO\). Vďaka rovnobežnosti s \(BO\) vieme tento uhol preniesť na súhlasný uhol k bodu \(O\). Tento uhol je susedný k uhlu \(AOB\), a preto má veľkosť \(2 \alpha\). Preto \[ \gamma = 2 \alpha - \beta. \qquad(2)\]

V podstate by nám v tomto momente stačilo vyjadriť napríklad \(\beta\) z rovnice 1 a nájsť maximum \(\gamma\) ako funkcie \(\alpha\). Vyjadrenie \(\beta\) by ale nebolo veľmi pekné a ani by neviedlo k o nič krajšiemu riešeniu. Preto sa touto cestou nevydáme⁶. To nám ale vôbec nebráni vnímať \(\beta\) ako nejakú funkciu \(\alpha\). Zatiaľ ju nijako bližšie nešpecifikujeme, ale vieme, že pre ňu platí rovnica 1.

Tým pádom sa nám ale podarilo vyjadriť \(\gamma\) ako funkciu jednej premennej⁷. Potrebujeme nájsť jej maximum. Na hľadanie extrémov funkcií jednej premennej máme veľmi silné kladivo – derivácie⁸.

Aby pre nejaký uhol \(\alpha\) nadobúdala funkcia \(\gamma (\alpha)\) extrém, musí byť jej derivácia podľa \(\alpha\) nulová. Derivovaním vzťahu 2 dostávame podmienku \[ 0 = \frac{\text{d} \gamma}{\text{d} \alpha} = 2 - \frac{\text{d} \beta}{\text{d} \alpha}. \qquad(3)\]

Potrebujeme ešte z rovnice 1 vyjadriť deriváciu \(\beta\) podľa \(\alpha\), preto zderivujme aj ju. Pritom nesmieme zabudnúť derivovať \(\sin \beta\) ako zloženú funkciu: \[ \begin{aligned} \frac{\text{d}\!\left(\sin \beta\right)}{\text{d} \alpha} &= n \frac{\text{d}\!\left(\sin \alpha\right)}{\text{d} \alpha}, \\ \cos \beta \frac{\text{d} \beta}{\text{d} \alpha} &= n \cos \alpha, \\ \frac{\text{d} \beta}{\text{d} \alpha} &= n \frac{\cos \alpha}{\cos \beta}. \end{aligned} \]

Po dosadení do (3) dostávame \[ 2 - n \frac{\cos \alpha}{\cos \beta} = 0 \implies 2 \cos \beta = n \cos \alpha. \qquad(4)\]

Spolu s upravenou rovnicou (1) tak riešime sústavu \[ \begin{aligned} 2 \cos \beta &= n \cos \alpha, \\ \sin \beta &= n \sin \alpha. \end{aligned} \]

Pri jej riešení by nám pomohlo, keby sme vedeli dať dokopy členy obsahujúce \(n\). Keď si spomenieme na vzorček \(\sin^2 \alpha + \cos^2 \alpha = 1\), ako dobrý nápad na úpravu vyzerá umocnenie oboch strán rovnice na druhú a sčítanie – zbavíme sa totiž premennej \(\alpha\): \[ 4 \cos^2 \beta + \sin^2 \beta = n^2. \]

Keď znova použijeme vzorček⁹ \(\sin^2 \alpha + \cos^2 \alpha = 1\), po pár úpravách prídeme k tomu, že \[ \begin{aligned} 4 \cos^2 \beta + (1 - \cos^2 \beta) &= n^2 \\ \cos^2 \beta &= \frac{n^2 - 1}{3} \\ \cos\beta &= \sqrt{\frac{n^2 - 1}{3}} \\ \beta &= \arccos\sqrt{\frac{n^2 - 1}{3}} = \ang{59;31;36}. \end{aligned} \]

Využitím (4) vieme ľahko nájsť aj \(\alpha\): \[ \begin{aligned} \cos \alpha &= \frac{2}{n} \cos\beta = \frac{2}{n} \sqrt{\frac{n^2 - 1}{3}} = \sqrt{\frac{4n^2 - 4}{3n^2}}, \\ \alpha &= \arccos \sqrt{\frac{4n^2 - 4}{3n^2}} = \ang{40;21;21}. \end{aligned} \]

Napokon z (2) máme hľadanú veľkosť uhla \(2 \gamma\): \[ 2\gamma = 4 \alpha - 2 \beta = 4 \arccos \sqrt{\frac{4n^2 - 4}{3n^2}} - 2 \arccos\sqrt{\frac{n^2 - 1}{3}} \doteq \ang{42;22;11}. \]

Na to, aby bol uhol dopadajúceho a vystupujúceho lúča čo najväčší, musíme na kvapku zasvietiť pod uhlom \(\beta = \ang{59;31;36}\). Uhol dopadajúceho a vystupujúceho lúča v tomto prípade bude \(2 \gamma = \ang{42;22;11}\).