5. Viete... Klin sa bodom vybíja vzorové riešenie

Na začiatok sa zamyslime, čo sa bude s klinom a hmotným bodom diať. Hmotný bod je ťahaný tiažou dole, no v ceste mu stojí naklonená rovina tvorená klinom. Tým samozrejme myslíme normálovú silu, ktorou klin pôsobí na bod, aby sa neprepadol cez jeho povrch. Newtonov 3. zákon však káže pre každú akciu, rovnako veľkú a opačnú reakciu, teda hmotný bod bude tlačiť opačnou silou na klin, čím spôsobí, že klin sa mu bude uhýbať zrýchlením, ktorého veľkosť označme \(A\). Podobne označme horizontálnu zložku zrýchlenia hmotného bodu \(a_x\).

Ak si teraz označíme horizontálnu zložku normálovej sily ako \(N_x\) a napíšeme Newtonov 2. zákon pre obe telesá v tomto smere, dostaneme \[ \begin{aligned} MA = N_x, \\ ma_x = N_x. \end{aligned} \]

Z toho jednoznačne vyplýva, že \[ ma_x = MA. \qquad(1)\]

Ďalej sa v riešení dá pokračovať aj cez energie, no my si ukážeme dve riešenia cez sily. Prvé sa dá veľmi ľahko aplikovať na všetky podobné príklady, druhé je síce čistejšie, no je ťažšie ho nájsť.

Riešenie 1 (pomocou fiktívnych (zotrvačných) síl a neinerciálnych sústav)

Predstavme si, že sa nachádzame vo vzťažnej sústave \(K\) spojenej s klinom. Klin však zrýchľuje vzhľadom na prednáškovú sálu, teda táto sústava je neinerciálna. V praxi to znamená, že na hmotný bod bude pôsobiť zotrvačná sila \(F_z = mA\), viď obrázok. Presne táto sila je to, čo nás tlačí do sedadla keď sedíme v zrýchľujúcom aute. Na hmotný bod v tejto sústave navyše pôsobia všetky sily, ktoré naň pôsobili v inerciálnej sústave (tiaž \(F_g\) a normálová sila \(N\)).

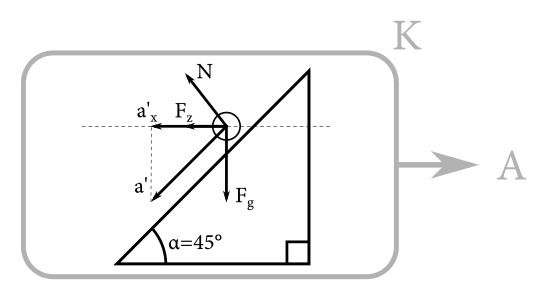
Prečo sa oplatí presunúť do zrýchľujúcej sústavy \(K\)? Predsa preto, že klin sa v tejto sústave nehýbe, a tak to vlastne vyzerá, akoby hmotný bod len skĺzol dole po naklonenej rovine zrýchlením \(a'\). Toto zrýchlenie nájdeme tak, že vypočítame priemet síl \(F_z\) a \(F_g\) na smer pohybu a použijeme Newtonov 2. zákon \[ ma' = F_g \sin \alpha + F_z \cos \alpha = \frac{1}{\sqrt{2}}(F_g + F_z) = \frac{1}{\sqrt{2}}\left(mg + mA\right). \]

Teraz chceme vyjadriť \(a_x\) pomocou \(a'\), aby sme mohli použiť (1). Prv nájdeme horizontálnu zložku \(a'_x\) zrýchlenia \(a'\) v sústave \(K\). Keďže \(a'\) smeruje pozdĺž naklonenej roviny, platí \[ a'_x = a'\cos \alpha = \frac{1}{\sqrt{2}}a'. \]

V horizontálnom smere sa teda bod pohybuje so zrýchlením \(a_x'\) vzhľadom na klin, ktorý sa pohybuje so zrýchlením \(A\) v opačnom smere vzhľadom na prednáškovú sálu. Tým pádom zrýchlenie \(a_x\) hmotného bodu vzhľadom na miestnosť nájdeme ako \[ a_x = a'_x - A = \frac{1}{2}\left(g - A\right). \]

Dosadením do rovnice (1) a úpravou dostaneme finálny výsledok \[ A = \frac{m}{m + 2M} g. \]

Riešenie 2

Avšak pokiaľ zo zrýchlení pociťujete závraty, riešiť sa dá aj v inerciálnej sústave. Prv sa zamyslíme po akej trajektórii sa bude bod pohybovať. V tom nám pomôže obrázok:

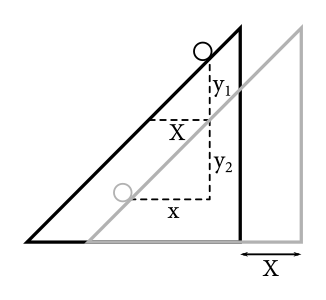
Vidíme, že keď sa bod pohne o \(x\) doľava a klin sa pohne o \(X\) doprava, tak na to, aby bod zostal na povrchu klinu, musí vertikálne klesnúť o \[ \begin{aligned} y &= y_1 + y_2 = X \tan \alpha + x \tan \alpha \\ &= X + x = x \left(1 + \frac{m}{M}\right), \\ \end{aligned} \] kde v poslednom kroku sme využili rovnicu 1, keďže \(x = \frac{1}{2}at^2\), \(X = \frac{1}{2}At^2\), \(mx = MX\). To ale znamená, že bod sa pohybuje po priamej trajektórii pod uhlom \(\beta\) voči horizontále, \[ \tan \beta = \frac{y}{x} = \left(1 + \frac{m}{M}\right). \]

V tejto (inerciálnej) sústave pôsobia na bod len dve sily, tiažová \(F_g\) a normálová \(N\). Aby sa bod hýbal po priamke, musí aj výsledná sila (vektorový súčet \(F_g+N\)) na bod smerovať po tejto priamke:

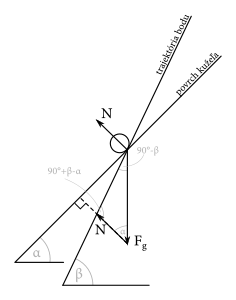
Všimnite si, že silu \(N\) sme prekreslili tak, aby začínala na konci \(F_g\) - tak sa graficky sčítavajú sily. Zo sínusovej vety v trojuholníku tvorenom vektormi \(N\) a \(F_g\) dostaneme \[ \begin{aligned} \frac{N}{\sin \left(\ang{90} - \beta\right)} &= \frac{F_g}{\sin \left(\ang{90} + \beta - \alpha\right)}, \\ N &= mg\frac{\cos \beta}{\cos \left(\alpha - \beta\right)} = mg\frac{\cos \beta}{\cos \alpha \cos \beta + \sin \alpha \sin \beta}, \\ N &= mg \frac{1}{\cos \alpha + \sin \alpha \tan \beta}, \\ N &= \sqrt{2} g \frac{mM}{m+2M}. \\ \end{aligned} \]

Teraz si už len stačí všimnúť, že horizontálna zložka normálovej sily je \[ N_x = N \sin \alpha = g\frac{mM}{m + 2M} \] a keďže \(N_x\) je jediná horizontálne pôsobiaca sila na klin, máme \(MA = N_x\), alebo \[ A = g\frac{m}{m+2M}. \]