3. Vive la résistance! vzorové riešenie

Zadanie

Nina odmieta počas koronakrízy stratiť kontakt s fyzikou. Zaumienila si, že bude klásť odpor. Aby lepšie vedela, aký odpor vlastne chce klásť, v priestore si predstavila dve skupiny uzlov, \(A\) a \(B\). Skupina uzlov \(A\) má \(a\) uzlov, skupina \(B\) má \(b\) uzlov. Následne každý uzol skupiny \(A\) spojila s každým uzlom skupiny \(B\) rezistorom s odporom \(R\).

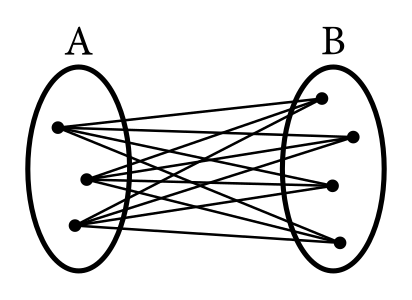
Ninu teraz zaujíma: Aký bude výsledný odpor medzi dvomi uzlami z rôznych skupín? A čo medzi dvomi uzlami tej istej skupiny?

Pre začiatok si zaveďme značenie, nech sa v tom celom ľahšie orientujeme. Uzly zo skupiny \(A\) nazvime \(A_1, A_2, \dots, A_a\); obdobne uzly zo skupiny \(B\) nazvime \(B_1, B_2, \dots, B_b\). Toľko pre začiatok.

Celé riešenie úlohy zvládneme jedným, veľmi jednoduchým trikom. Ak majú dva body v obvode rovnaký potenciál, netečie medzi nimi prúd. Netečie medzi nimi prúd ani v prípade, že sú prepojené vodičom, či rezistorom. Ako v ktoromsi svojom učebnom texte k FKS napísal kedysi Juro Tekel, keď je medzi takými dvoma bodmi vodič, môžeme ho kľudne rozpojiť, nakoľko by tadiaľ aj tak prúd netiekol; ak tam bol rezistor, môžeme ho predať a kúpiť si žuvačku.

Ako však možno zistiť, že dva body majú rovnaký potenciál, keď už je to také užitočné? (Aj vy máte radi žuvačky?) Existuje niekoľko trikov so zrkadlovým prevracaním schémy či počítaním napätí a teda potenciálov v jednotlivých bodoch. A potom existuje jedna naozaj jednoduchá úvaha. Ak máme v obvode dva body, do/z ktorých tečú rovnaké prúdy, ak sú to body symetrické a ich výmenou by sa nič nezmenilo, vtedy majú rovnaký potenciál.

Merajme teraz odpor medzi bodmi \(A_1, A_2\). Ak sa poriadne pozrieme na obvod, zistíme, že všetky body z \(B\) majú rovnaký potenciál – ak by sme napríklad medzi sebou prehodili body \(B_{42}\) a \(B_{47}\), situácia v obvode sa nezmení. A úplne to isté platí o bodoch \(A_3, A_4, ..., A_a\) – tiež majú všetky rovnaký potenciál. Rozpájanie v našom prípade príliš nehrozí – veď žiadne dva body z \(A\), resp. z \(B\) nie sú vzájomne spojené. Môžeme však všetky body s rovnakým potenciálom spojiť do jedného uzla! Pozrime, čo nám to spraví so schémou – tu už pamätajme, že každá z elíps predstavuje jeden bod.

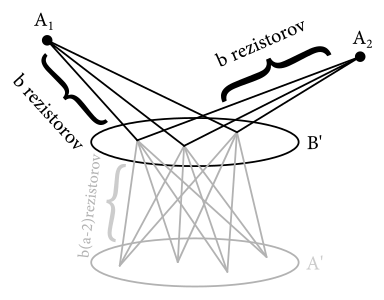
Vidíme, že z uzla \(A_1\) vedie do veľkého uzla s \(b\) bodmi \(b\) paralelne zapojených rezistorov, teda odpor medzi týmito dvoma uzlami je \(\frac{R}{b}\). Toto celé je k tomu pripojené ešte raz sériovo (medzi uzlami \(b\) a \(A_2\)), teda platí, že odpor medzi dvoma bodmi z \(A\) je rovný \(R_{AA} = \frac{2R}{b}\). Samozrejme, úplne symetricky, ak by sme vzali dva body z \(B\), odpor medzi nimi by bol rovný \(R_{BB} = \frac{2R}{a}\)

Ak budeme merať odpor medzi bodmi \(A_1\) a \(B_1\), opäť vieme scucnúť do jedného bodu \(A'\) všetky uzly z \(A\) a do bodu \(B'\) všetky body z \(B\) (samozrejme, okrem \(A_1\) a \(B_1\) - body \(A', B'\) budú potom obsahovať \(a-1\), resp. \(b-1\) pôvodných uzlov). Jeden rezistor vedie medzi bodmi \(A_1-B_1\); \(b-1\) rezistorov medzi bodmi \(A_1-B'\); \((a-1)(b-1)\) rezistorov medzi bodmi \(A'-B'\) a napokon \(a-1\) rezistorov medzi bodmi \(A'-B_1\). Opäť si môžeme nakresliť obrázok.

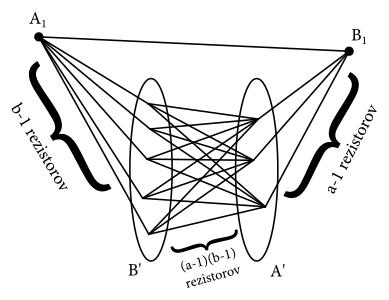
Jednoducho vieme povedať, že medzi \(A_1, B_1\) sú dve paralelné vetvy, jedna s odporom \(R\), druhá, zložitejšia, s odporom \(R_x\), ktorý dopočítame. Vieme však povedať, že celkový odpor medzi našimi dvoma bodmi je \(R_{AB} = \frac{1}{\frac{1}{R}+\frac{1}{R_x}}\), čo si vieme napísať i krajšie, tento výraz však platí pre práve dve paralelná odporné vetvy: \(R_{AB} = \frac{RR_x}{R+R_x}\). Odpor \(R_x\) predstavuje tri sériovo zapojené paralelné skupiny rezistorov, teda \(R_x = \frac{R}{b-1}+\frac{R}{(a-1)(b-1)}+\frac{R}{a-1}\), toto vieme upraviť na spoločného menovateľa, na tvar \[ R_x = \frac{(a-1) + 1 + (b-1)}{(a-1)(b-1)} R = \frac{a+b-1}{(a-1)(b-1)}R. \]

Toto vieme dosadiť do nášho vzťahu \[ \begin{aligned} R_{AB} = \frac{RR_x}{R + R_x} = \frac{\frac{a+b-1}{(a-1)(b-1)}R^2}{R+\frac{a+b-1}{(a-1)(b-1)}R} = \frac{\frac{a+b-1}{(a-1)(b-1)}R}{\frac{a+b-1+(a-1)(b-1)}{(a-1)(b-1)}} = \frac{a+b-1}{a+b-1+(a-1)(b-1)}R = \frac{a+b-1}{ab}R. \end{aligned} \]

A teda po nepekných, no jednoduchých úpravách dostaneme odpor medzi jedným z bodov z \(A\) a jedným z bodov z \(B\) je rovný \(R_{AB} = \frac{a+b-1}{ab}R\).