5. Blší kolotoč vzorové riešenie

Zadanie

Vladkov kariérny postup v komerčnej sfére bol taký rýchly, že si po pár mesiacoch mohol kúpiť nový superšportiak. Auto dokáže rovnomerne zrýchliť z \(0\) až na \(\SI{300}{\kilo\metre\per\hour}\) za desať sekúnd. Má klasický analógový rýchlomer, ciachovaný s dielikom \(\ang{1} / \SI{1}{\kilo\metre\per\hour}\), pričom jeho ručička je dlhá \(\SI{5}{\centi\metre}\). Ciferník rýchlomera je umiestnený tak, že os ručičky je vodorovná a polohe priamo hore zodpovedá rýchlosť \(\SI{150}{\kilo\metre\per\hour}\).

Na konci ručičky rýchlomera navyše sedí drobná blška. Aké maximálne preťaženie bude cítiť počas zrýchľovania, keď Vladko dupne na plyn?

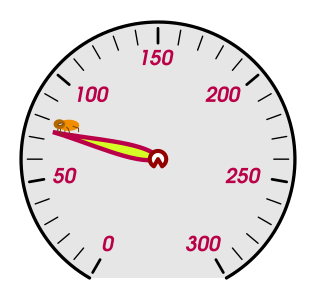
Započítajte všetky efekty. Ak je niektorý zanedbateľne malý, nestačí to len uviesť, treba to aj ukázať.

Než sa pustíme do riešenia samotnej úlohy, objasnime si, čo sa nás vlastne zadanie pýta. Máme spočítať preťaženie. Preťaženie je v istom zmysle len obyčajné zrýchlenie, avšak udáva sa v násobkoch tiažového zrýchlenia \(g\). Na človeka v pokoji na Zemi tak pôsobí preťaženie \(\SI{1}{g}\), technicky vzaté teda nejde o preťaženie. Ak ale sedí napríklad v rakete a smeruje na Mesiac, pocíti pri vzlete výrazne väčšie preťaženie.

Inak to nie je ani s blškou vo Vladkovom aute. Našou snahou bude identifikovať, s akým zrýchlením sa pohybuje blška. V tomto bode isto začínajú blikať výstražné kontrolky vo vašich hlavách, ktoré sa pýtajú „A v ktorej vzťažnej sústave?“. Skutočne, táto otázka je kľúčová pre vyriešenie úlohy. Blška sa nachádza v neinerciálnej sústave pevne spojenej s tachometrom. Ručičku tachometra pritom považujeme za jednu z osí tejto sústavy, zvyšné dve kolmé osi (ako je srdcu blízke) orientujeme v smere kolmom na tachometer a v smere otáčania sa ručičky tachometra. V tejto sústave nás bude zaujímať preťaženie (lebo v tejto sústave sa blška cíti byť). Definujeme ešte inerciálnu sústavu, tá bude spojená so Zemou. Neskôr sa zamyslíme, či je takáto definícia dobrá :).

Pokúsme sa lepšie charakterizovať, čo sa vlastne deje v neinerciálnej sústave. Po prvé, v neinerciálnej sústave pôsobí rovnaká reálna sila, ako v inerciálnej. Touto silou je sila tiažová, jej zrýchlenie už poznáme – \(\vec{g}\).

Po druhé si zahrajú tzv. neinerciálne (fiktívne) sily. Tieto sily sú štyri. Zrýchlenie, ktoré cíti blška, sa dá vyjadriť nasledovným vzťahom: \[ \vec{a}'=\frac{\vec{F}}{m}-\vec{a_0}-2\vec{\omega}\times \vec{v}' - \vec{\omega}\times(\vec{\omega}\times \vec{r}') - \vec{\varepsilon}\times \vec{r}' \]

Komplikovaný vzťah by sme mali napísaný, poďme si ho aj vysvetliť, pekne člen po člene. Najprv však dodajme, že čiarkované vektory sú vzhľadom na neinerciálnu sústavu.

Prvý člen je \(\frac{\vec{F}}{m}\). \(\vec{F}\) je tu reálna sila, ktorá pôsobí na blšku, vydelená hmotnosťou blšky nám dáva to slávne tiažové zrýchlenie. Tento člen je teda identicky rovný \(\vec{g}\).

Druhý člen je \(-\vec{a_0}\). Tento člen zodpovedá za zrýchlenie neinerciálnej sústavy vzhľadom na inerciálnu – ide o zrýchlenie auta. Zo zadania vieme, že má veľkosť \(a_0 = \frac{\SI{300}{\kilo\meter\per\hour}}{\SI{10}{\second}}=\frac{25}{3} \si{\meter\per\second\squared}\). Toto zrýchlenie prislúcha sile, ktorú normálne poznáme pod názvom zotrvačná. Vektoruchtivý čitateľ si akiste domyslí, že toto zrýchlenie má smer proti (pozor na to mínus!) pohybu auta. Je to presne tá „sila, ktorá nás tlačí do sedačiek“ keď na to dupneme :).

Tretí člen, \(-2\vec{\omega}\times\vec{v}'\), je slávny aj pod názvom Coriolisova sila – teda presnejšie jej príslušné zrýchlenie. \(\vec{\omega}\) je tu uhlová rýchlosť ručičky tachometra, \(\vec{v}'\) je rýchlosť blšky v sústave spojenej s tachometrom. Nakoľko sa však blška v tejto sústave (vzhľadom na ručičku tachometra) vôbec nehýbe, tento člen je rovný nule.

Štvrtý člen, \(-\vec{\omega}\times\left(\vec{\omega}\times\vec{r}\right)\), si častejšie predstavíme ako tzv. odstredivé zrýchlenie, zrýchlenie odstredivej sily. Pripomeňme si že \(\vec{r}'\) je vektor v sústave tachometra smerujúci k blške, teda je to vektor ručičky tachometra. Vektor uhlovej rýchlosti, smerovo zhodný s vektorom otáčania (určený známym pravidlom pravej ruky), je kolmý na \(\vec{r}'\), a vektorové súčiny (alebo iné pravidlo, tiež pravej ruky) nám prezradia, že smer tejto sily je smer ručičky tachometra, smer „od stredu“ tachometra, odkiaľ sa aj berie názov odstredivá. Pripomeňme, že tento smer sa počas pohybu mení! Ktorý smer nás vo výsledku bude zaujímať si povieme až trochu neskôr. Veľkosť uhlovej rýchlosti je \(\frac{\ang{300}}{\SI{10}{\second}}=\frac{\frac{5}{3}\pi}{\SI{10}{\second}}=\frac{\pi}{6}\si[per-mode=reciprocal]{\per\second}\), ručička tachometra má dĺžku \(\SI{0,05}{\meter}\), teda veľkosť tohoto člena je \(\frac{\num{0,05}\pi^2}{\num{36}} \si{\meter\per\second\squared} = \frac{5\pi^2}{\num{3600}} \si{\meter\per\second\squared}\). To už je celkom málo, ale stále to budeme brať v úvahu.

Piaty člen je \(-\vec{\varepsilon}\times\vec{r}'\). Príslušná sila sa nazýva Eulerova. Vidíme, že \(\vec{\varepsilon}\), ktorý je uhlovým zrýchlením tachometra, je zo zadania rovný nule, teda aj celý člen je nulový.

Teraz už vieme, ktoré neinerciálne členy skutočne hrajú rolu – zotrvačné a odstredivé zrýchlenie. Pridá sa aj reálne tiažové zrýchlenie. Najväčšia veľkosť výsledného zrýchlenia by bola vtedy, keby všetky vektory smerovali rovnakým smerom. To však dosiahnuť nevieme – jediné, čo vieme ovplyvniť, je smer vektora odstredivého zrýchlenia. Vieme ho sklopiť čo najviac do smeru tiažovej sily (do smeru zotrvačnej sily ho sklopiť nevieme, na tú bude vždy kolmý), a to vtedy, keď ručička tachometra smeruje čo najviac nadol - pri rýchlostiach \(0\) a \(\SI{300}{\kilo\meter\per\hour}\). Zo zadania poznáme uhol, ktorý pri takejto rýchlosti (napr. tej väčšej) vektory zvierajú, dokážeme teda vektor odstredivého zrýchlenia rozložiť do smeru tiažovej sily a smeru kolmého na obe zvyšné zrýchlenia. Sčítaním vektorov v tomto prípade dostaneme číselný výsledok približne rovný (uvažujúc \(g=\SI{9,81}{\meter\per\second\squared}\)) \(a'=\SI{12,8726}{\meter\per\second\squared} =\SI{1,3122}{g}\).

Teraz by sme si mohli povedať, že to stačí. Avšak zadanie nás urguje, aby sme každý efekt buď započítali, alebo prehlásili za neškodný. Čo sme teda ešte nezapočítali? Uviedli sme Zem ako inerciálnu sústavu, čo tak celkom nebude. Pre potreby nášho výpočtu je to ale dobré priblíženie, ako uvidíme nižšie.

Zem nie je rovná. Zem je guľa a auto po nej ide nejakou rýchlosťou, čo znamená, že sa pohybuje s dostredivým zrýchlením. Proti tomu je rovnaká „odstredivá“ sila, ako sme už opísali, ale jej zrýchlenie sa nám tentoraz ľahšie vyjadrí ako \(\frac{v^2}{R}\), a smer má proti tiažovému zrýchleniu. Ak ho započítame aj pri maximálnej rýchlosti \(\SI{300}{\kilo\meter\per\hour}\), opravu na tiažové zrýchlenie robí na treťom desatinnom mieste. Väčšej chyby sa teda už dopúšťame nezobrazím presnej hodnoty \(g\). Oprava na výsledku vzhľadom na tento efekt sa prejaví na štvrtom desatinnom mieste, číselný výsledok bude \(\SI{1,3122}{g}\). Tu príde na rad otázka, čo už zanedbať a čo ešte nie. Ak ste zanedbali tento efekt, treba si uvedomiť, že efekt odstredivej sily na tachometri je rádovo rovnaký. Potom by bolo potrebné zanedbať aj ten. Je dôležité zanedbávať „všade rovnako“, nemôžeme z dvoch rovnako vážnych efektov jeden zarátať a druhý vynechať. :)

Zem, ako guľa, sa točí okolo svojej osi. Našťastie, tu trochu zavádzam, toto sme započítali :). Tento efekt je už započítaný v hodnote tiažového zrýchlenia. Teda nás nemusí trápiť, že by sme ho obišli – ale nech tu explicitne je. V hodnote ale nie je započítané, že auto sa hýbe – teda tu bude pôsobiť Coriolisova sila vzhľadom na otáčanie sa Zeme. Asi ale nikoho neprekvapí, že tento efekt je skutočne zanedbateľný. Inak by sme predsa museli kompletne prerobiť naše ponímanie tiažového zrýchlenia pre telesá pohybujúce sa klasickými rýchlosťami :).

Zem obieha okolo Slnka. Tu si dovolíme tvrdiť, že tento efekt nespôsobuje preťaženie voči Zemi. Presne preto pre teleso v pokoji uvažujeme preťaženie \(\SI{1}{g}\).

Efektov sa dá nájsť skutočne veľa, tie vyššie opísané by sa dali považovať za najviac súvisiace s úlohou. Z vašich riešení chcem ešte oceniť počítanie odporu vzduchu blšky pri pohybe na tachometri, tento efekt skutočne nenapadol ani mne :)

Pozn.: V tomto vzorovom riešení neuvádzame odvodenie vzťahu pre neinerciálne sily. Rovnako to ani nepovažujeme za nutnú súčasť riešenia, teda za neprítomnosť odvodenia body strhávať nebudeme. Ak by vás zaujímalo odvodenie, s trochou porozumenia vektorom a deriváciám odporúčam text prednášok Doc. RNDr. Vladimíra Černého, v ktorom nájdete podrobné odvodenie.