Zadanie
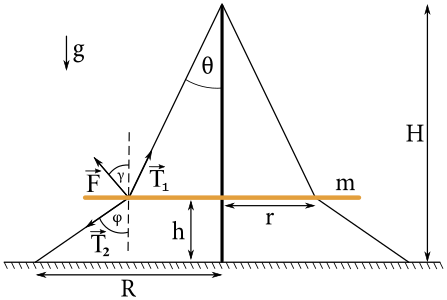
Inšpirované svetoznámejšími miestami, rozhodlo sa Kocúrkovo vybudovať veľký nápis „KOCÚRKOVO“ na neďalekom vŕšku. V záujme odbúrania byrokracie spojenej s verejným obstarávaním bola zákazka rozdelená na desať menších, a jedna zo stavieb písmen „O“ sa dostala svojho času do zaujímavej fázy. Písmeno v tvare sústredného medzikružia si celou svojou hmotnosťou \(m\) hovie vo vodorovnej polohe na dvoch dokonale tuhých lanách, pričom každé z nich je jedným z kocov pripevnené na stožiar výšky \(H\) taký, že leží na osi písmena, a druhým o zem vo vzdialenosti \(R\) od päty stožiara. Hovenie tohoto písmena s vnútorným polomerom \(r\) prebieha vo výške \(h\) nad zemou. Ako veľkou silou pôsobí každé z lán na písmeno?

Na to, aby sme vypočítali sily lán, ktoré pôsobia na písmeno O potrebujeme napísať rovnice, v ktorých budú tieto sily vystupovať. Hneď na začiatok sa zbavíme jednej rovnice. Keďže písmeno je po celý čas vo vodorovnej polohe, tak vieme že moment sily je nulový a teda sila od ľavého lana sa rovná sile od pravého). Tu sa však musíme na chvíľu pozastaviť a urobiť zopár predpokladov. Táto úloha sa dala preto riešiť viacerými spôsobmi, ktoré závisia od toho aké predpoklady uvažujeme. Predstavme si, že písmeno O tlačí na lano silou \(-\vec{F}\) a teda lano tlačí na písmeno rovnako veľkou, ale opačne orientovanou silou \(\vec{F}\), ktorej veľkosť chceme vypočítať. Ak by sme poznali smer sily \(\vec{F}\), tak by sme vedeli z geometrie písmena a stožiara napísať rovnicu, v ktorej by vystupovala. Avšak na to, aby mohla takáto situácia nastať musia byť splnené nasledovné predpoklady: hrany písmena musia byť zaoblené a nezanedbateľne hrubé (uvažujeme 3D objekt nie 2D) a trenie medzi lanom a písmenom je nulové. Uvažujme malý kúsok nehmotného lana. Keďže náš kúsok lana sa nijak nenaťahuje ani netrhá, vieme z toho usúdiť, že veľkosti síl, ktoré pôsobia na lano z susedných malých kúskov musia byť rovnako veľké. Z týchto vlastností vyplýva, že sila \(F\) má smer daný osou uhla, ktorý zviera dolná a horná časť lana.1
Skúsme teraz nájsť rovnicu, v ktorej bude vystupovať sila \(\vec{F}\). Asi najjednoduchšia cesta bude napísať si rovnicu, ktorá popisuje všetky sily pôsobiace na písmeno. Okrem sily od lana nám na písmeno pôsobí ešte aj gravitačná sila, avšak treba si uvedomiť, že všetky tieto sily majú rôzny smer, takže s nimi budeme pracovať ako s vektormi. Zavedieme si x-ovú os rovnobežne s písmenom O (prechádzajúcou cez body, v ktorých je písmeno pripevnené)a y-ovú os prechádzajúcu tyčou. Teraz si rozložme jednotlivé sily do smerov nami zadefinovaných osí (samozrejme bude potrebné použiť trochu trigonometrie).
Všeobecne je naša rovnica zadaná ako
\[ \vec{F_g} + \vec{F} = \vec{0}. \qquad(1)\]
V smere osi y
\[ -mg + 2F_y = 0 \qquad(2)\]
a v smere osi x
\[ F_x - F_x = 0. \qquad(3)\]
Tretia rovnica (3) nám nič nové nepovie, iba, že \(F_x=F_x\). V druhej rovnici (2) je \(F\) vynásobené 2, pretože písmeno držia dve laná. Na pravých stranách našich 3 rovníc je 0 (\(\vec{0}\)), pretože písmeno si iba hovie a nehýbe z čoho vyplýva, že celková sila je nulová.
Poďme si teraz vyjadriť silu \(F\) pomocou zadaných hodnôt. Sila \(F\) pôsobí pod uhlom \(\gamma\) vzhľadom na y-ovú os, takže môžeme napísať \(F_y = F\cos(\gamma)\). Zároveň vieme, že \(\gamma = \frac{\theta - \varphi}{2} + 90\). Rovnicu (2) vieme prepísať ako
\[ -mg + 2F\cos(\gamma) = 0, \qquad(4)\]
kde
\[ \cos(\gamma) = \sin(\frac{\varphi - \theta}{2}) = \frac{\sqrt{1 - \cos(\varphi)\cos({\theta}) - \sin(\varphi)\sin({\theta})}}{\sqrt{2}}. \]
Takže výsledok je
\[ F = \frac{mg}{2\cos(\gamma)} = \frac{mg}{2} \cdot \frac{\sqrt{2}}{\sqrt{1 - \cos(\varphi)\cos({\theta}) - \sin(\varphi)\sin({\theta})}}, \qquad(5)\]
pričom \(\cos(\theta) = \frac{H-h}{\sqrt{r^2+(H-h)^2}}\), \(\sin(\theta) = \frac{r}{\sqrt{r^2+(H-h)^2}}\), \(\cos(\varphi) = \frac{h}{\sqrt{(R-r)^2+h^2}}\) a \(\sin(\varphi) = \frac{R-r}{\sqrt{(R-r)^2+h^2}}\).
Pár poznámok na záver:
Viacerí z vás úlohu pochopili tak, že bolo potrebné vypočítať sily od spodnej a hornej časti lana. Ak si napíšeme rovnicu pre všetky sily pôsobiace na naše písmeno dostaneme všeobecne
\[ -mg + 2T_{1y} - 2T_{2y} = 0, \qquad(6)\]
avšak v našom prípade platí, že \(T_1 = T_2 = T\) z dôvodov, ktoré sme uviedli už na začiatku, preto dostávame rovnicu
\[ -mg + 2T\cos(\theta) - 2T\cos(\varphi) = 0, \qquad(7)\]
z toho vyplýva, že
\[ T = \frac{mg}{2(\cos(\theta) - \cos(\varphi))}. \qquad(8)\]
Ďalšiu malú poznámku by som venovala tomu, že k rovnici (4) sa dalo dopracovať aj cez momenty síl. Keďže si môžme vybrať ľubovoľný bod, vyberme si napr. bod, v ktorom sa lano dotýka písmena. Vieme, že v tomto bode je moment sily nulový, a preto môžme napísať rovnicu pre momenty síl ako
\[ \vec{r} \times \vec{F_g} + 2\vec{r} \times \vec{F} = 0, \qquad(9)\]
po rozpísaní vektorového súčinu dostávame
\[ -mgr + 2F\cos(\gamma)r = 0, \qquad(10)\]
alebo \(-mgr + 2T\cos(\theta)r - 2T\cos(\varphi)r = 0\)
po vydelení \(r\) dostávame rovnicu (8).
Na záver by som chcela spomenúť ešte iný spôsob riešenia tejto úlohy, a to pomocou virtuálnych prác. Pri tomto postupe nepotrebujeme robiť žiadne ďalšie predpoklady na rozdiel od prvého prístupu. Majme teda všeobecný prípad, čiže písmeno nemusí byť na vnútornom okraji zaoblené a medzi lanom a písmenom môže pôsobiť trecia sila. To znamená, že vo všeobecnosti sily \(T_1\) a \(T_2\) nie sú rovnaké. To, čo potrebujeme nájsť je uhol \(\gamma\), ktorý nepoznáme. Povedzme teda, že písmeno si už hovie vo svojej rovnovážnej polohe. Princíp virtuálnych prác nám hovorí, že ak vykonáme malé myslené posunutie v okolí rovnovážnej polohy, tak celková práca je nulová. Čo to ale znamená v našom prípade? Na bod, v ktorom sa lano dotýka obruče, pôsobí sila od lana \(T_1 \sin(\theta) - T_2 \sin(\varphi) = -\Delta T\). To však spôsobí napätie v písmene O a preto sa začne defromovať, takže si predstavme, že tento bod sa posunie o \(\delta r\) (zväčšenie vzdialenosti o \(\delta r\) medzi tyčou a bodom dotyku), avšak v dôsledku toho písmeno klesne o malú výšku \(\delta h\). Čiže práca, ktorú by sme vykonali pri posunutí \(\delta r\) sa rovná zmene potenciálnej energie a preto môžme napísať rovnosť
\[ 2\Delta T \delta r = mg \delta h. \qquad(11)\]
\(\Delta T\) je vynásobené faktorom 2, pretože na písmene sa nachádzajú dva body dotyku.
Ak by sme teda našli vzťah medzi \(\delta r\) a \(\delta h\), tak by sme vedeli túto rovnicu vyriešiť. Ale ako nájsť takúto rovnicu? Svietielkom na konci tunela by mohla byť konštantná dĺžka lán bez ohľadu na polohu písmena.
\[ l = \sqrt{(H - h)^2 + r^2} + \sqrt{h^2 + (R - r)^2} \qquad(12)\]
\[ l = \sqrt{(H - h + \delta h)^2 + (r + \delta r)^2} + \sqrt{(h - \delta h)^2 + (R - r -\delta r)^2} \qquad(13)\]
Celkom nepekný výraz, avšak nezabúdajme, že pracujeme s malými posunutiami, preto prichádza na rad zanedbávanie. Vieme, že platí nasledujúce priblíženie
\[ \sqrt{x + \delta x} = \sqrt{x}\sqrt{1 + \frac{\delta x}{x}} \approx \sqrt{x}(1 + \frac{\delta x}{2x}) = \sqrt{x} + \frac{\delta x}{2\sqrt{x}}. \qquad(14)\]2
Použime túto aproximáciu v rovnici (13) a zanedbajme členy rádu \(\delta x^2\). Dostaneme tak rovnicu
\[ l = \sqrt{(H - h)^2 + r^2} + \frac{(H - h)\delta h + r \delta r}{\sqrt{(H - h)^2 + r^2}} + \sqrt{h^2 + (R - r)^2} - \frac{h\delta h + (R - r) \delta r}{\sqrt{h^2 + (R - r)^2}}. \qquad(15)\]
Ak teraz dáme do rovnosti rovnice (12) a (15) dostávame
\[ \frac{(H - h)\delta h + r \delta r}{\sqrt{(H - h)^2 + r^2}} = \frac{h\delta h + (R - r) \delta r}{\sqrt{h^2 + (R - r)^2}}, \qquad(16)\]
pričom v rovnici spoznávame trigonometrické funkcie, ktoré sme popísali už pri vzťahu (5). Vyjadrime si \(\delta r\) a dosaďme do rovnice (11)
\[ T_1 \sin(\theta) - T_2 \sin(\varphi) = \frac{mg}{2} \frac{\sin(\theta) - \sin(\varphi)}{\cos(\theta) - \cos(\varphi)}. \qquad(17)\]
Takže teraz máme dve rovnice o dvoch neznámych - (17) spolu aj s rovnicou síl vo vertikálnom smere (7). Po ich vyriešení dostávame prekvapujúci výsledok
\[ T_1 = T_2 = \frac{mg}{2}\frac{1}{\cos(\theta) - \cos(\varphi)}, \]
čo znamená, že aj bez našich predpokladov sa sily \(T_1\) a \(T_2\) rovnajú, takže dostávame rovnaké riešenie ako v prvom prípade.
Náš malý kúsok lana tlačí na písmeno malou silou \(\delta \vec{F}\). Ak by sme zistili silu \(\delta \vec{F}\), potom by už len stačilo spočítať všetky takéto malé sily a tak by sme zistili celkovú silu \(\vec{F}\). Sčítaním síl od susediacich dielikov lana na náš malý kúsok získame silu \(\delta \vec{F}\). Dotyčnicové zložky sa vyrušia a teda zostane nám iba zložka smerujúce kolmo na povrch písmenka. Ak teraz opäť vektorovo sčítame všetky takéto malé zložky \(\delta \vec{F}\), tak dostaneme celkovú silu \(\vec{F}\) smerujúca v smere osi uhla, ktorý zviera dolná a horná časť lana.↩︎
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.