7. Radi(k)álne riešenie vzorové riešenie

Zem sa okolo Slnka pohybuje po elipse, pričom Slnko leží v jednom z ohnísk. V tejto úlohe sa tak budeme musieť vysporiadať s pohybom po elipse¹. Aby sme ho vedeli popísať, potrebujeme vedieť popísať polohu Zeme vzhľadom na Slnko. Musíme preto vybrať nejaké vhodné súradnice. Milovníkov kartézskych súradníc hneď sklameme, pretože tie nepoužijeme. Ako to už býva pri pohybe po niečom kruhovitom, oplatí sa používať polárne súradnice. Ich stred si umiestnime do Slnka, teda do ohniska elipsy.

Polohu Zeme vzhľadom na Slnko tak budeme popisovať dvojicou \((r,\theta)\), kde \(r\) predstavuje vzdialenosť Zeme a Slnka a \(\theta\) je orientovaný uhol, ktorý zviera úsečka spájajúca Zem a Slnko s úsečkou, ktorá spája ohniská elipsy (v jednom z nich je Slnko). Za kladný uhol určíme ten, v ktorom Zem obieha okolo Slnka.

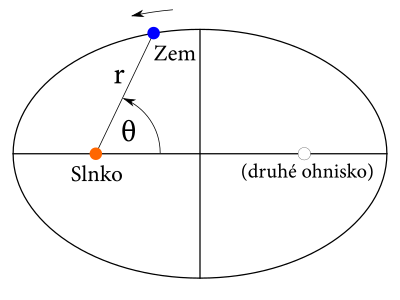
Keď už máme zadefinované polárne súradnice, pripomeňme si, že obe zložky polohy \(r\) aj \(\theta\) sa budú neustále meniť. Na druhej strane úloha od nás chce zistiť, kedy je radiálna rýchlosť najväčšia. V reči týchto súradníc to znamená, že chceme vedieť, kedy sa \(r\) najrýchlejšie mení².

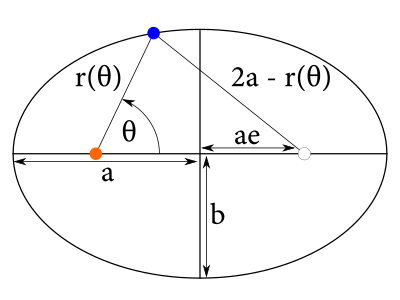
My navyše vieme, že máme danú elipsu. Preto poznáme dĺžky jej osí \(a\), \(b\), a teda aj jej excentricitu \(e\)³. Pre danú elipsu tak musíme byť schopní vyjadriť závislosť \(r\) od \(\theta\).

Preto uvažujme trojuholník tvorený ohniskami a Zemou. Vzdialenosť Zem-Slnko je \(r(\theta)\). Vzdialenosť ohnísk je \(2ae\). Napokon, pre každý bod elipsy platí, že súčet jeho vzdialeností od ohnísk je rovný \(2a\). Preto je vzdialenosť Zeme od druhého ohniska elipsy rovná \(2a-r(\theta)\). Z kosínusovej vety pre zmienený trojuholník tak dostávame:

\[\begin{aligned} (2a-r(\theta))^2&=r(\theta)^2+(2ae)^2-2(2ae)r(\theta)\cos\theta\\ 4a^2-4ar(\theta)+r(\theta)^2&=r(\theta)^2+4a^2e^2-4aer(\theta)\cos\theta\\ a-r(\theta)&=ae^2-er(\theta)\cos\theta\\ r(\theta)&=\frac{a(1-e^2)}{1-e\cos\theta} \end{aligned}\]

Tým máme vyjadrenú vzdialenosť radiálnej vzdialenosti \(r\) od uhla \(\theta\). Derivovaním tohto vzťahu podľa času, dostávame vzťah pre radiálnu rýchlosť⁴:

\[\dot r(\theta)=\frac{a(1-e^2)(e \sin\theta)\dot \theta}{(1-e\cos\theta)^2}\]

Z praktických dôvodov, ktoré uvidíme neskôr, si tento vzťah upravme tak, aby obsahoval aj \(r(\theta)\):

\[\dot r(\theta)=\frac{r(\theta) e \sin(\theta) \dot \theta}{1-e\cos\theta}\]

Pozorný čitateľ si už mohol všimnúť dve veci. Prvou z nich je, že sa nám vo vzťahu objavila \(\dot \theta\), teda uhlová rýchlosť v danom čase. Jej sa v ďalšom priebehu budeme chcieť zbaviť. Druhá vec, ktorú si čitateľ mohol všimnúť, je, že doteraz bolo toto vzorové riešenie len o matematike. Zišlo by sa tak použiť nejakú fyziku. Fyzikov Pavlovov reflex by sa mal pri úlohe s planétami hneď snažiť používať Keplerove zákony. Teraz príde náramne vhod druhý Keplerov zákon⁵. Jedna z formulácií druhého Keplerovho zákona je, že obsah plochy, ktorú opíše sprievodič za nejaký malý čas \(\mathrm{d}t\), je rovnaká pre každý takýto časový interval. Matematicky, \(\dot S=\frac{\mathrm{d}S}{\mathrm{d}t}\) je konštanta.

Aby sme vedeli využiť, čo nám povedal druhý Keplerov zákon, potrebujeme vypočítať \(\frac{\mathrm{d}S}{\mathrm{d}t}\). V tomto svete nekonečne malých vyzerá táto plôška ako rovnoramenný trojuholník s ramenami dĺžky \(r(\theta)\) a uhlom oproti základni \(\mathrm{d} \theta\). Tento trojuholník má preto obsah:

\[\mathrm{d}S=\frac{1}{2}r^2(\theta) \sin \mathrm{d} \theta\]

Keďže \(\mathrm{d} \theta \rightarrow 0\), tak \(\sin \mathrm{d} \theta = \mathrm{d} \theta\) a môžeme písať:

\[\frac{\mathrm{d}S}{\mathrm{d}t}=\frac{1}{2}r^2(\theta) \frac{\mathrm{d} \theta}{\mathrm{d} t} = \frac{1}{2}r^2(\theta) \dot \theta\]

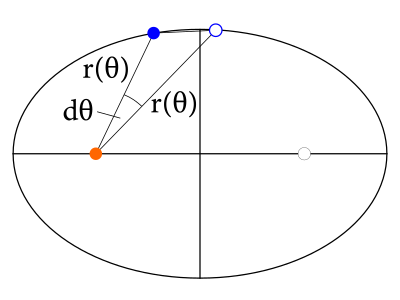
Podľa druhého Keplerovho zákona je preto \(\frac{1}{2}r^2(\theta) \dot \theta\) konštantné. Keď nasčítame takéto plôšky pre všetky časové intervaly \(\mathrm{d}t\) z periódy obehu Zeme \(T\), dostaneme ⁶:

\[\frac{S}{T}=\frac{1}{2}r^2(\theta) \dot \theta\]

Navyše o elipse vieme \(S=\pi a b\) a o Zemi vieme \(T\). Do vyjadrenia pre \(\dot r(\theta)\) sa nám zíde vedieť hodnotu \(r(\theta) \dot \theta\), tak ju odtiaľto vyjadrime:

\[r(\theta) \dot \theta = \frac{2 \pi a b}{r(\theta) T}\]

A dosaďme do vyjadrenia pre \(\dot r(\theta)\), do ktorej hneď potom dosaďme aj vyjadrenie \(r(\theta)\):

\[\begin{aligned} \dot{r}(\theta) &= \frac{2 \pi a b e \sin\theta}{T(1-e\cos\theta)r(\theta)}\\ \dot{r}(\theta) &= \frac{2 \pi b e \sin\theta}{T(1-e^2)} \end{aligned}\]

Konečne máme vyjadrenie radiálnej rýchlosti, v ktorom je jediná premenná uhol \(\theta\). Ostatné členy sú konštanty. Najväčšia radiálna rýchlosť sa preto dosahuje v extrémnych hodnotách \(\sin \theta\). To sú hodnoty \(1\) a \(-1\), ktoré sa líšia len v tom, že v jednom prípade sa takou rýchlosťou Zem približuje a v druhom vzďaľuje Slnku. Tieto hodnoty sa nadobúdajú vtedy, keď \(\theta = \frac{\pi}{2}\) a keď \(\theta = \frac{3\pi}{2}\).

Takže najvyššia radiálna rýchlosť sa dosahuje vtedy, keď sa Zem nachádza v takom bode, že úsečka spájajúca Zem a Slnko je kolmá na hlavnú os jej eliptického pohybu.