7. Satelitné sledovanie vzorové riešenie

Predtým, ako sa pustíme do riešenia, si skúsme napísať v bodoch ako rozumieme úlohe:

1. Protóny budú vyletovať zo Slnka do všetkých smerov rovnako, a teda ich počet na jednotku plochy bude klesať so štvorcom vzdialenosti. (Podobne ako svetelné lúče.)
2. Zrážky sú nepružné, preto sa energia nezachováva. Dokonca, protóny sa kvôli nepružnosti „nalepujú na satelit“, čím sa hmotnosť satelitu zvyšuje.¹ Na zistenie toho, ako sa bude satelit urýchľovať nám pomôže zákon zachovania hybnosti, ktorý platí aj pri neelastických zrážkach.
3. Hmotnosť jedného protónu je omnoho menšia ako hmotnosť satelitu. Toto je dôležité v tom, že nám to môže zjednodušiť inak škaredé výrazy.
4. Tým, že na satelit budú dopadať protóny, budú ho urýchlovať smerom od Slnka. Ako sa bude od Slnka vzďaľovať, počet dopadajúcich protónov sa bude zmenšovať. To bude zase meniť jeho urýchlovanie, čo bude meniť jeho vzdialenosť… Mohli by sme pokračovať donekonečna. Ako sa dá takáto vec zrátať? Jednou možnosťou je to nasimulovať v počítači (na to musíme však poznať presné číselné údaje, čo nevieme) alebo, našťastie, matematika prináša aparát, ktorý je vytvorený na riešenie takýchto problémov – diferenciálne rovnice. Nakoniec teda môžeme čakať, že budeme musieť spočítať nejakú diferenciálnu rovnicu.

Toľko ku prvotným insightom, teraz hor sa do riešenia!

Začnime tým, že sa pozrieme na zrážky. Ak po \(k\)-tom náraze bude mať satelit rýchlosť \(u_k\), jeho celková hmotnosť bude \(M + km\) a pre \((k+1)\)-ty náraz platí zákon zachovania hybnosti \[ (M + km) u_k + m v = \left(M + \left(k+1\right)m\right) u_{k+1} \] Ak vyjadríme \(u_{k+1}\) a následne odpočítame z oboch strán \(u_k\), aby sme získali zmenu rýchlosti; po premasírovaní výrazov dostaneme: \[ u_{k+1} - u_k = \frac{m }{M+ (k+1)m} \cdot (v-u_k) \] Všimnime si teraz čo nám táto rovnica hovorí. V prvom rade v menovateli máme \(M + (k+1)m\), čo je celková hmotnosť satelitu po \((k+1)\)-om náraze (teda aj so všetkými nalepenými protónmi ). Keďže ale hmotnosť protónu je veľmi malá, je vlastne jedno, či budeme používať hmotnosť po alebo pred nárazom tohto jedného protónu. Preto môžeme výraz v menovateli interpretovať ako hmotnosť pri \(k\)-tom náraze \(M_k\) \[ u_{k+1} - u_k \approx \frac{m}{M_k} \cdot (v - u_k) \] Ďalej v druhej časti výrazu vidíme \((v-u_k)\), čo je relatívna rýchlosť satelitu a protónov. Totiž, čím rýchlejšie sa bude satelit pohybovať, tým slabší efekt budú mať jednotlivé nárazy. Prvú časť máme za sebou – vieme, čo sa stane pri jednej zrážke.

Koľko protónov narazí do satelitu každú sekundu, ak sa nachádza vo vzdialenosti \(r\)? Protóny len tak nezanikajú, a teda platí štandardný argument²: počet protónov, čo dopadne na plochu \(S\) vo vzdialenosti \(r\) je úmerný pomeru plochy \(S\) a sféry s polomerom \(r\). Matematicky zapísané: \[ N = \frac{S}{4\pi r^2} n \] Toto by však platilo len pre stacionárny satelit – pre unikajúci je v skutočnosti počet narazených protónov menší! Predstavte si to takto: kebyže sa satelit hýbe tak rýchlo ako protóny, žiadne na ňu reálne nedopadnú, satelit ide predsa „s prúdom“. Ak chceme naozaj spočítať narazený počet protónov za čas \(\Delta t\), od počtu \(N \Delta t\) musíme odpočítať počet protónov vo vyšrafovanej ploche na obrázku, lebo im satelit uletel a oni ho nestihli dobehnúť.

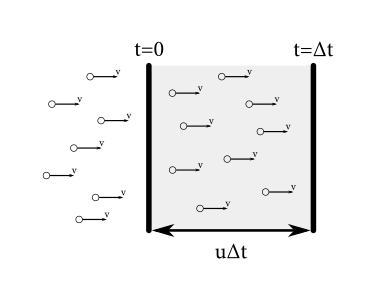
Keďže dĺžka plochy je \(u \Delta t\), protóny potrebujú čas \(\frac{u \Delta t}{v}\) na jej prejdenie, a teda od predošlého počtu musíme tieto protóny odpočítať; t.j. odpočítať \(N \frac{u \Delta t}{v}\). Počas krátkeho časového úseku \(\Delta t\) ich takto narazí \(N \Delta t (1-u/v)\). Preto zrýchlenie satelitu bude: \[ a(t) = \frac{u(t + \Delta t) - u(t)}{\Delta t} = (N\Delta t (1-u/v)) \frac{u_{k+1} - u_k}{\Delta t} \] Po dosadení za pravú stranu dostaneme rovnicu: \[ u'(t) = \frac{N(r) m}{M(t) v} (v- u(t))^2 \]

kde \(M(t) = \int_0^t N(r) m \,\mathrm dt\) a zároveň \(N(r) = \frac{Sn}{4\pi r^2}\). Toto je veľmi komplikovaná diferenciálna rovnica, ktorá zrejme nemá pekné analytické riešenie. Čo môžeme spraviť je zjednodušiť ju nejakými aproximáciami. Jednou z nich je, že môžeme predpokladať, že hmotnosť satelitu sa veľmi nebude meniť v čase. Je totiž nepravdepodobné, že by jeho hmotnosť výrazne narástla. Druhou approximáciou bude, že jeho vzdialenosť od Slnka sa veľmi nezmení (t.j., satelit je tak ďaleko od Slnka, že zmena polohy bude zanedbateľná voči jeho počiatočnej vzdialenosti od Slnka). Preto aproximujeme \(N(r)\) tak, že za \(r\) dosadíme iba jeho počiatočnú polohu. Takto sa nám písmenká \(N, M\) zmenia na konštanty a mi dostávame sympatickejšiu diferenciálnu rovnicu: \[ u'(t) = \frac{N m}{M v} (v- u(t))^2 \] Takáto rovnica sa dá riešiť celkom jednoducho. Rozpíšeme \(u'(t) = \frac{\mathrm du}{\mathrm dt}\) a separujeme premenné: \[ \frac{\mathrm du}{(v - u)^2} = \frac{Nm}{Mv} \mathrm dt \] a zintegrujeme obe strany. Integračné limity nastavíme tak, že začínajú od \(t=0\) a \(u=0\), lebo na počiatku sa satelit nehýbe. ³ \[ \int_0^u \frac{\mathrm du}{(v-u)^2} = \frac{Nm}{Mv} \int_0^t \mathrm dt \]

\[ \frac{1}{v-u} - \frac{1}{v} = \frac{Nm}{Mv} t \]

Nakoniec dostaneme: \[ u(t) = v\frac{Nmt}{{Nmt} + M} \]

kde \(N = \frac{Sn}{4\pi r_0^2}\).

Komentár ku riešeniam: Viacerí ste sa snažili zarátať aj gravitačné pole Slnka, čo vôbec nie je zlý krok, no výsledok bol, že diferenciálnu rovnicu vám to len skomplikovalo ešte viac – tak, že záchranou bolo iba numerické riešenie. V našom vzoráku sme ju nespomenuli, lebo aj tak neskôr zanedbávame zmenu vzdialenosti od Slnka, čím by bol jej efekt presne vyrušený odstredivou silou. Ak by sme spravili iné zanedbanie – kebyže zanedbáme rýchlosť rakety voči rýchlosti protónov a zmenu polohy tam necháme, gravitačná sila by bola nezanedbateľnou časťou rovnice. Pri hodnotení vašich riešení sme najmä dbali na správnosť fyziky pri nárazoch protónov a taktiež na konzistentnosti zanedbaní. Táto úloha bola naozaj veľmi ťažká a každému, kto sa ju aj pokúsil riešiť patrí gratulácia.