6. Reálna fyzika vzorové riešenie

Na začiatok sa asi patrí zdôrazniť, že v celom vzoráku budeme študovať metastabilitu a fázové prechody spôsobené zmenou tlaku. V škole ste sa asi stretli s tými, ktoré sú spôsobené zmenou teploty. V tomto prípade však bude naozaj názornejšie študovať izotermické procesy. Na výsledku to nič nezmení.

Rovnica, ktorú sme uviedli v zadaní sa nazýva van der Waalsova stavová rovnica a popisuje vzťah medzi stavovými veličinami v neideálnom plyne. Rozdiely oproti stavovej rovnici ideálneho plynu sú dva. Ako prvé to je parameter \(b\), ktorý označuje minimálny objem molekúl, na ktorý ich možno stlačiť. A ďalej to je parameter \(a\), ktorý zohľadňuje korekciu k tlaku spôsobenú interakciou medzi molekulami. Vzhľadom na obe tieto korekcie možno aspoň kvalitatívne popísať van der Waalsovou stavovou rovnicou okrem plynu aj kvapaliny v blízkosti fázového rozhrania kvapalina - plyn. To v tejto úlohe aj patrične využijeme.

Začnime teda tým, že zavedieme objem jedného molu častíc \(v=\frac{V}{n}\). Potom prejde van der Waalsova stavová rovnica do tvaru \[ p= \frac{RT}{v-b} - \frac{a}{v^2}, \] v ktorom sa nám bude lepšie hovoriť o termodynamických fázach. Veď \(n\) predsa nepoznáme a fáza je aj tak určená stavovými veličinami \(p\), \(v\), a \(T\). Načrtnime si teraz závislosť tlaku tekutiny od objemu, pre hodnoty stavových veličín blízko fázového prechodu.

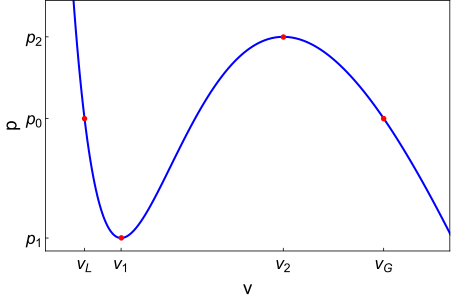
Graf si žiada pomerne podrobné vysvetlenie. Krivka na prvý pohľad ukazuje ako sa budú pri izotermickom deji, napríklad kompresii, správať zvyšné stavové veličiny. Je zjavné, že pri tlakoch menších ako \(p_1\) bude mať tekutina veľký objem, takže bude v plynnej fáze. Naopak pri tlakoch väčších ako \(p_2\) sa bude realizovať kvapalná fáza. Pre tlaky medzi \(p_1\) a \(p_2\) van der Waalsova stavova rovnica hovorí, že tekutina môže mať tri objemy. Čudné, že? Pravdou je, že v tomto intervale tlakov sú stabilné dve fázy, kvapalná aj plynná. Pre objemy menšie ako \(v_1\) je to kvapalná fáza a pre objemy väčšie ako \(v_2\) zas plynná fáza. Oblasť medzi týmito objemami, kde je krivka \(p(v)\) rastúca, je nefyzikálna. Predstavte si, že v nejakej oblasti tekutiny vznikne fluktuácia s vyššou hustotou častíc, a teda \(v\) lokálne klesne. To by znamenalo, že klesne tlak, čo povedie k ďalšiemu rastu hustoty v tejto oblasti, pretože naokolo je tlak tekutiny vyšší. Podobne fluktuácie s nižšou hustotou ako priemerná sa budú ďalej vyprázdňovať. Takýto systém sa teda spontánne rozpadne na zmes hustých a riedkych oblastí. Odborne sa tomu hovorí spinodálna dekompozícia.

Vráťme sa ale späť k otázke fázového prechodu. Kedy teda nastáva? Odpoveďou je, že pri dostatočne nízkej teplote, pre ktorú sme načrtli závislosť tlaku od objemu, kdekoľvek v intervale tlakov \(\langle p_1, p_2 \rangle\). A prečo sa potom štandardne kreslia vo fázových diagramoch ostré rozhrania medzi fázami? To je preto, že do fázových diagramov sa zakresľujú oblasti, v ktorých sú fázy globálne stabilné, to znamená s najmenšou (voľnou) energiou. Tomu sa tu však nebudeme venovať, nám stačí vedieť, že takýto fázový prechod medzi stavmi v termodynamickej rovnováhe by nastal na našom grafe pri tlaku \(p_0\). Vtedy má kvapalná a plynná fáza rovnakú energiu a tekutina môže pri tlaku \(p_0\) nadobúdať objem kdekoľvek medzi \(v_L\) a \(v_G\).

Keď to teda zhrnieme, kvapalná fáza je globálne stabilná pri tlakoch väčších ako \(p_0\) a plynná fáza je globálne stabilná pri tlakoch menších ako \(p_0\). Čo sa teda deje na tých zvyšných intervaloch, kde sú fázy stabilné? Ako už asi tušíte, tam sú iba lokálne stabilné, alebo teda metastabilné. To znamená, že tieto fázy môžu existovať, ale prežijú iba malé fluktuácie v hustote, respektíve energii. Akákoľvek väčšia fluktuácia spôsobí fázový prechod do globálne stabilnej fázy. Kvapalnej fáze medzi tlakmi \(p_1\) a \(p_0\) sa hovorí prehriata kvapalina a naopak plynnej fáze medzi tlakmi \(p_0\) a \(p_2\) sa hovorí podchladený plyn.

No dobre, a čo ak je teplota veľmi vysoká? Vtedy bude krivka \(p(v)\) monotónne klesať. Tam bude pre daný tlak existovať iba jeden prípustný objem a teda iba jedna fáza a žiadne fázové rozhranie. A to je presne to, čo by sme mali aj čakať. Pri teplotách a tlakoch vyšších ako sú tie kritického bodu sa plynná a kvapalná fáza nedajú rozlíšiť, a systém sa nachádza vo fáze superkritickej tekutiny.

V tomto momente by sme už mali rozumieť tomu, čo hovorí van der Waalsova stavova rovnica o fázových prechodoch a metastabilite. Zostáva nám tie oblasti/hranice metastability už iba nájsť. Presnejšie, pre hranicu metastability kvapalnej a plynnej fázy musíme postupne určiť body \(\left[p_1, v_1\right]\) a \(\left[p_2, v_2\right]\) pri rôznych teplotách. To už je práca pre cvičené opice. Zafixujeme \(T\) a začneme binárne vyhľadávať objem \(v\), pre ktorý tlak \(p\) dosahuje lokálne extrémy. Tí šikovnejší na to použijú počítač, a tí ešte šikovnejší funkciu \(p(v)\) zderivujú položia rovnú nule a vyriešia kubickú rovnicu.

Keďže som ten najšikovnejší, ja som si to zderivoval a kubickú rovnicu za mňa vyriešil počítač. Výsledky sú zakreslené okrem \(p\)–\(v\) diagramu aj v štandardnom \(p\)–\(T\) diagrame. Keďže hodnoty \(a\) a \(b\) sa môžu meniť a my ich nepoznáme, patrí sa na osi grafov vynášať hodnoty stavových veličín ako násobky prirodzených hodnôt systému, t.j. tlaku \(\frac{a}{b^2}\), objemu \(b\), a teploty \(\frac{1}{R} \frac{a}{b}\). Modrou farbou je v grafoch vyznačená hranica metastability kvapalnej fázy, oranžovou je hranica metastability plynnej fázy, a žltou farbou je vyznačená celá oblasť, v ktorej može byť tekutina podľa van der Waalsovej stavovej rovnice metastabilná. Termodynamické fázové rozhranie tam samozrejme zakreslené nie je, keďže to z van der Waalsovej stavovej rovnice nevieme zistiť.

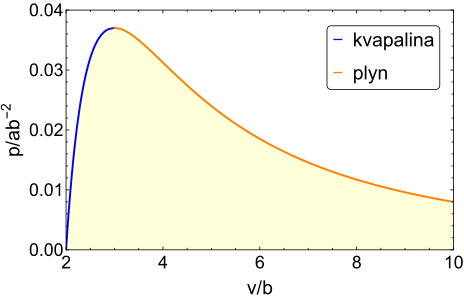
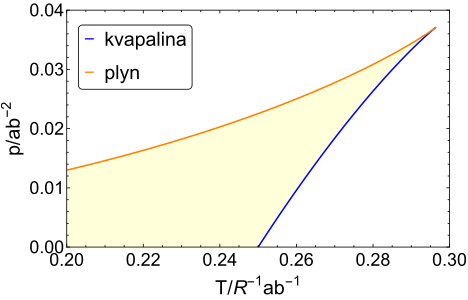
Na záver upozorníme ešte na dve veci. Hodnoty stavových veličín v kritickom bode sa dajú zistiť z van der Waalsovej stavovej rovnice presne. Vyjde \(p_c = \frac{1}{27} \frac{a}{b^2}\), \(T_c = \frac{8}{27} \frac{a}{Rb}\). V skutočnosti pri nízkych teplotách a vysokých tlakoch nebude kvapalina metastabilná. V tejto oblasti van der Waalsova stavová rovnica neplatí a na termodynamický popis systémov treba použiť úplne iné teórie, keďže sa tu zväčša realizuje pevná fáza hmoty.