3. Samoštúdium vzorové riešenie

Začnime tým, že si uvedomíme, čo sa tu deje. Akonáhle začneme nafukovať balónik, tak začne rásť jeho objem, pričom jeho hmotnosť sa takmer nemení. To znamená, že efektívne zväčšujeme vztlakovú silu pôsobiacu na balónik, pričom tiažová sila sa nemení. V istom momente je vztlaková sila dostatočne veľká na to, aby balónik vyplával. Ak budeme pokračovať v nafukovaní, balónik sa bude viac a viac vynárať, až konečne dosiahne nami požadovaný pomer ponorenej a vynorenej časti. Pekne priamočiare, že? Tak si to poďme zrátať!

Podľa Archimedovho zákona na teleso ponorené do kvapaliny pôsobí vztlaková sila, ktorej veľkosť je rovná tiaži vytlačenej kvapaliny. Nech \(k\)-tina objemu balóna je ponorená. Potom z Archimedovho zákona dostávame \[ kV\varrho=m\textrm{,} \qquad(1)\] kde \(V\) je objem balónika, \(m\) je jeho hmotnosť (aj s pieskom) a \(\varrho\) je hustota vody. Odtiaľ vieme priamo vyjadriť objem balónika čisto len pomocou známych veličín a dopočítať objem vzduchu v balóniku nie je problém, takže sa zdá, že máme vyhrané. Ale je tomu tak naozaj? Nezabúdajme, že naša nádoba je síce dostatočne veľká, čo sa týka plochy, no má len obmedzenú hĺbku. Patrilo by sa teda ešte overiť, či sa do nej takto nafúknutý balónik vôbec zmestí. Na to potrebujeme zistiť, ako hlboko musí byť balónik ponorený, aby bola ponorená práve \(k\)-tina jeho objemu, resp. ako vysoko prečnieva nad hladinou.

Nech výška guľového odseku prečnievajúca nad hladinu je \(v\). Objem vynorenej časti je zrejme \(\left(1-k\right)V\), kde \(V=\frac{4}{3}\pi r^{3}\). Zároveň tento objem vieme vyjadriť čisto len pomocou jeho výšky a polomeru gule¹ \[ \left(1-k\right)V=\pi v^{2}\left(r-\frac{v}{3}\right)\textrm{.} \qquad(2)\] Dosadiac príslušný výraz za \(V\) sa vieme po drobných úpravých dopracovať k nasledovnej rovnici: \[ k=1-\frac{3}{4}\left(\frac{v}{r}\right)^{2}+\frac{1}{4}\left(\frac{v}{r}\right)^{3}\textrm{.} \qquad(3)\] Jedinou neznámou v tejto rovnici je \(v\), ktoré sa práve snažíme zistiť. Nanešťastie ide o kubickú rovnicu, ktorú nevieme jednoducho vyriešiť. Preto to trochu obídeme. Zaveďme si parameter \[ p=\frac{v}{r}\textrm{,} \qquad(4)\] ktorý vyjadruje pomer medzi výškou balónika nad hladinou a jeho polomerom. Potom možno uvedenú rovnicu prepísať na: \[ k=1-\frac{3}{4}p^{2}+\frac{1}{4}p^{3}\textrm{.} \qquad(5)\] Táto rovnica dáva do súvisu parameter \(k\) s parametrom \(p\), takže ich môžeme medzi sebou kedykoľvek zamieňať. Odteraz budeme teda \(k\) považovať za funkciu parametra \(p\) a budeme to zapisovať \(k\left(p\right)\).

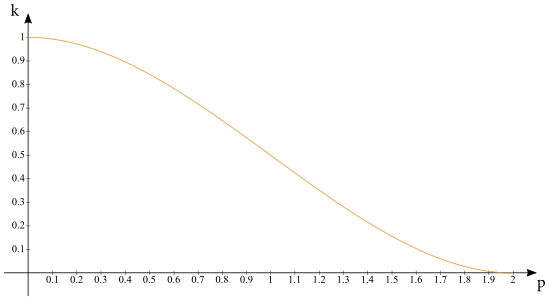
Vráťme sa späť k Archimedovmu zákonu. Vyjadrime si z neho polomer balónika \[ r\left(p\right)=\sqrt[3]{\frac{3m}{4\pi\varrho k\left(p\right)}}\textrm{.} \qquad(6)\] Výška guľového odseku nad hladinou je potom z definície \[ v\left(p\right)=pr\left(p\right)=p\sqrt[3]{\frac{3m}{4\pi\varrho k\left(p\right)}} \qquad(7)\] a hĺbka, do ktorej siaha balónik je \[ h\left(p\right)=2r\left(p\right)-v\left(p\right)=\left(2-p\right)r\left(p\right)=\left(2-p\right)\sqrt[3]{\frac{3m}{4\pi\varrho k\left(p\right)}}\textrm{.} \qquad(8)\]

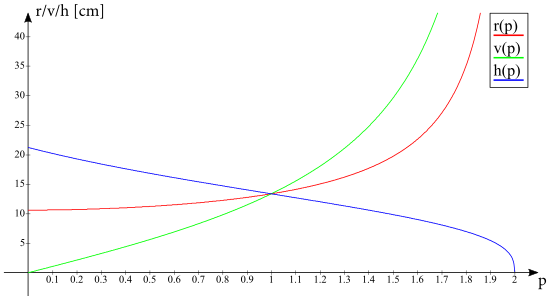
Teraz už máme všetko potrebné na to, aby sme vedeli túto úlohu vyriešiť. Začnime časťou a). Nad hladinou má vytŕčať \(\frac{1}{4}\) balónika. To znamená, že \(k=\num{0.75}\). Zistíme, aká hodnota parametra \(p\) tomu zodpovedá. Keďže to nevieme urobiť analyticky, urobíme to numericky. Vykreslíme si závislosť \(k\left(p\right)\) a z grafu odčítame príslušnú hodnotu. Zisťujeme, že \(p\approx\num{0.6527}\). Teraz už vieme dopočítať príslušnú hĺbku ponoru podľa Rovnica 8 \(h\approx\SI{15.7303}{\centi\metre}\), čo je menej než hĺbka vody v nádobe, takže všetko je v poriadku. Nič nám teda nebráni v tom, dopočítať objem vzduchu v balóniku, ktorý je rovný samotnému objemu balóniku zmenšenému o objem piesku, čiže \[ V_{a}=\frac{4}{3}\pi r^{3}-\frac{m}{\rho}\textrm{,} \qquad(9)\] kde \(r\approx\SI{11.6754}{\centi\metre}\) je polomer balónika vypočítaný podľa Rovnica 6 a \(\rho\) je hustota piesku. Konečne dostávame \(V_{a}\approx\SI{3.809}{\litre}\).

Presuňme sa na časť b). Tu budeme postupovať úplne rovnako. Nad hladinou má teraz pretŕčať \(\frac{1}{5}\) objemu, teda \(k=\num{0.8}\). Numericky nájdeme, že tomu zodpovedá hodnota parametra \(p\approx\num{0.5743}\). Hĺbka ponoru je potom \(h\approx\SI{16.2915}{\centi\metre}\). A tu narážame na problém. Hĺbka vody v nádobe je predsa len \(\SI{16}{\centi\metre}\)! Čo to presne znamená?

Vráťme sa v našich úvahách úplne na začiatok. Tam sme hovorili, že balónik nafukujeme, až v istom momente vypláva, a potom pokračujeme v nafukovaní, až vytŕča požadovaná časť balónika. Tento predpoklad teraz ale zjavne nie je splnený, a teda balónik musí pretŕčať o požadovanú časť objemu ešte pred tým, než sa odlepí odo dna. To nám paradoxne uľahší prácu, pretože Rovnica 5 musí byť splnená stále a my predsa vieme, že ponorených je presne \(h=\SI{16}{\centi\metre}\) balónika. Z definície totiž \(v=pr\) a zároveň \(h+v=2r\), teda balónik treba nafúknuť na polomer \(r=\frac{h}{2-p}\approx\SI{11.2226}{\centi\metre}\). Tomu zodpovedá podľa Rovnica 9 objem vzduchu \(V_{a}\approx\SI{3.064}{\litre}\).