4. Šarmantná fotka vzorové riešenie

Zadanie

To, že Marcel je vášnivý fotograf je známa vec. No, kto z vás vedel, že Marcel mimo iné vlastní aj pilotný preukaz? A teda keď sa tieto dva koníčky skombinujú, tak vzniknú aj takéto šarmantné fotky.

Keďže už aj tak mal Marcel čo robiť s riadením lietadla a fotením, tak už netuší, kde fotka vznikla – vie len, že kdesi nad Bratislavou. Čo najpresnejšie určte zemepisné súradnice a nadmorskú výšku odkiaľ bola fotka odfotená.

Pri riešení úlohy môžete používať výpočtový softvér.

Keby ste boli vekovo na úrovni Kvíka, okrem dinosaurov a prvého koncertu Helenky Vondráčkovej by ste si pamätali, že podobná úloha tu už kedysi bola. V nej sa šikovným spôsobom dalo využiť to, že sme mali k dispozícii viaceré význačné body a že sme na nej poznali horizont. Tu to však také jednoduché nie je.

Aj keď riešenie je určite jednoznačné (fotka je skutočná a fotoaparát niekde byť musel), bez ďalšej informácie ho veľmi presne zistiť nedokážeme. Môžeme si síce otvoriť nejaký vhodný softvér, napríklad Google Earth, pokúsiť sa nastaviť podobný pohľad a odčítať polohu – takáto metóda je však značne nepresná, závisí od zvoleného zorného poľa a ani po fyzikálnej stránke nie je práve hodnotná.

V obrázku však určitá dodatočná informácia skrytá je: budovy bývajú spravidla postavené tak, že ich steny sú zvislé. Keďže nie sme v Pise, ale niekde nad Bratislavou, môžeme predpokladať, že toto platí. Ak si na chvíľu odmyslíme, že Zem nie je dokonalá guľa, predĺženia hrán stien ležia na priamkach, prechádzajúcich stredom Zeme. Na fotke však sa samozrejme nemusia zobraziť ako zvislé, čo dokážeme využiť.

Nakreslime si niekoľko takýchto priamok na fotku, ako keby ich fotoaparát mohol vidieť, a predpokladajme, že ich vidíme aj vnútri Zeme. Stačia dve, pre názornosť ale skúsme aspoň tri. Na polohe striktne vzaté nezáleží¹, ale intuitívne by nám malo byť zrejmé, že bude najlepšie, ak budú na fotke čo najďalej od seba, aby sme minimalizovali chyby. Zvoľme si napríklad os vysielača na Kamzíku, os komína teplárne Polianky pri Dúbravke a najvyšší mrakodrap na Dlhých dieloch.

Tieto virtuálne priamky sa pretínajú v strede Zeme². Na fotografii sa nám pretnú kdesi pod spodným okrajom, čo nám na prvý pohľad veľmi nepomohlo… aspoň kým si neuvedomíme, že na toto miesto by sa takisto zobrazil stred Zeme. Viac ako stred nás bude zaujímať miesto na povrchu, ktoré sa nachádzalo presne pod Marcelovým lietadlom. To však leží na spojnici fotoaparátu a stredu Zeme, teda na fotke je na rovnakom mieste. Kde sa však toto miesto nachádza v skutočnom trojrozmernom svete?

To je jednoduché: pozrime sa opäť na tieto čiary a všimnime si, po akých miestach na povrchu prechádzajú na fotke. Ak ich pospájame – napríklad v Google Earth – a odignorujeme členitosť terénu, dostaneme znovu priamky, ale tentokrát na povrchu Zeme. Tam, kde sa pretnú, leží miesto priamo pod fotoaparátom, ktoré si označíme \(P\). Takto dostaneme súradnice približne \(\ang{48.1293}\) N, \(\ang{17.0714}\) E, blízko začiatku legendárnej diaľnice D1.

Zemepisnú šírku a dĺžku poznáme, čo však s výškou? Tu si pomôžeme nie zvislou priamkou, ale vodorovnou plochou. Opäť budeme hľadať nejakú dostatočne veľkú – dobre poslúži strecha Matfyzu alebo PriFUKu (olympijské obdĺžniky vľavo dolu) alebo Dúbravka. Nakreslime si na toto miesto na fotku štvorec a predstavme si, že zodpovedajú skutočné miesta posprejujeme farbou (aby sme neskôr, až nás chytia policajti, nemuseli veľa čistiť v rámci verejnoprospešných prác, postačí nám jeho obrys).

Ak je plocha dosť rovná, jeho spodná strana bude v skutočnosti úsečka, navyše kolmá na líniu pohľadu. Odmeriame jej skutočnú dĺžku a tiež dĺžku strany štvorca na obrázku – u nás to je \(\SI{394}{\metre}\) a \(\SI{176}{px}\). Jeden pixel teda v tejto vzdialenosti zodpovedá asi \(\SI{2.2}{\metre}\). Ľavá strana (na fotke zvislá) však kvôli perspektíve bude v skutočnosti podstatne dlhšia, u nás až \(\SI{894}{\metre}\). Natiahla sa totiž pri zobrazení pod uhlom \(\alpha\). Ak si to nakreslíme, zistíme, že preň bude musieť platiť vzťah \[ \cos\alpha = \frac{\SI{394}{\metre}}{\SI{894}{\metre}}. \]

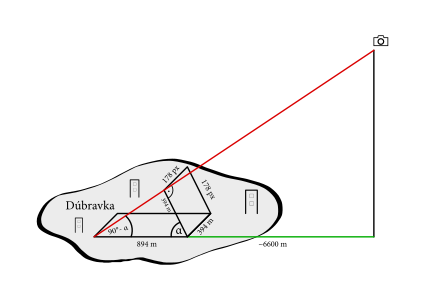
Nás zaujíma doplnok tohoto uhla do \(\ang{90}\), čo je uhol, pod ktorým by pozorovateľ v rohu štvorca videl lietadlo, merané od jeho horizontu. Po vyčíslení zistíme, že \(\ang{90} - \alpha \doteq \ang{26}\). Vzdialenosť od vrchola štvorca³ po bod \(P\) vieme opäť odmerať v Google Earth. V našom prípade je to asi \(\SI{6600}{\metre}\). Jednoduchou trigonometriou dopočítame, že lietadlo muselo byť vo výške asi \(\tan{\ang{26}} \cdot \SI{6600}{\metre} \doteq \SI{3240}{\metre}\) nad úrovňou štvorca, čo je nejakých \(\SI{3450}{\metre}\) nad morom. Vzorový súbor vo formáte kmz vyzerá takto.

Možných postupov je samozrejme viac. Miesto plochej Dúbravky by sme mohli použiť zvislý komín, alebo odmerať viacero kolmých úsečiek na fotke a v skutočnosti a dofitovať správnu geometrickú vzdialenosť.