2. Čo ti hrabe? (vzorové riešenie) - Fyzikálny korešpondenčný seminár

Zadanie

Majo minule nemal svoj deň. Po dlhom a náročnom upratovaní FKS miestnosti pri odchode stúpil na hrable. Ako už býva zvykom, hrable to vzali osobne a pokúsili sa vraziť Majovi do čela. Majo ako správny fyzik nezaváhal a položil si nasledujúcu otázku: „Ak sa rýchlo neuhnem, akou rýchlosťou ma hrable trafia do čela?“ Pomôže Majovi a odhadnite túto rýchlosť aj Vy. Potrebné údaje o hrabliach tiež čo najpresnejšie odhadnite alebo si ich nájdite.

Začnime analýzou skúmanej situácie spojenou s budovaním potrebného vedomostného aparátu. Rovnako ako na hrable, tak aj na Maja, ktorého hmotnosť odhadneme na $m_\text{M} = \SI{70}{\kilo\gram}$, pôsobí tiažová sila určená známym vzťahom $\vec{F} = m\vec{g} \doteq \SI{700}{\newton}$. Pri rotačnom pohybe je analógiou druhého Newtonovho zákona: \[ \vec{F} = \frac{\Delta \vec{p}}{\Delta t } = m\cdot\frac{\Delta \vec{v}}{\Delta t } = m\vec{a} \] vzťah \[ \vec{M} = I\vec{\epsilon}. \]

Analógia funguje nasledovne. - Ekvivalentom zvyčajnej sily $\vec{F}$ pre rotačný pohyb je moment sily $\vec{M} = \vec{r} \times \vec{F}$. Keď sa obmedzíme len na veľkosti¹, tak $M = rF_\bot = r F \sin\alpha$ (značenie podľa Obr. moment-sily ).

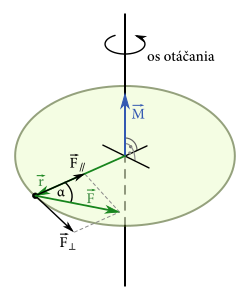
$G$ Moment sily $\vec{M}$ pôsobiaci na bod vo vzdialenosti $\vec{r}$ od osi otáčania pri pôsobení sily $\vec{F}$. Os otáčania aj moment sily sú kolmé na rovinu určenú vektormi $\vec{r}$ a $\vec{F}$.

Ekvivalentom hmotnosti $m$, je moment zotrvačnosti $I$. Hovorí nám, ako náročné je uviesť teleso do otáčavého pohybu vzhľadom na os rotácie. Moment zotrvačnosti bodu hmotnosti $m$ s kolmou vzdialenosťou od osi otáčania $r$ má hodnotu $I = mr^2$. Ľubovoľné teleso si vieme porozdeľovať na hmotné miničiastočky. Celkovým momentom zotrvačnosti potom bude súčet momentov zotrvačností týchto miničiastočiek. Aby sme sa však vyhli pokročilej matematike (integrálnemu počtu), výsledok pre tenkú tyč hmotnosti $m$ a dĺžky $L$ s osou otáčania kolmou na tyč a prechádzajúcou koncom tyče si môžeme nájsť napríklad na wikipédii: \[ I = \frac{1}{3}mL^2. \] Hrable si aproximujeme súčtom dvoch navzájom kolmých tyčí: kratšej² s dĺžkou $l_1 = \SI{10}{\centi\metre} = \SI{0.1}{\metre}$ a hmotnosťou $m_1 = \SI{0.5}{\kilo\gram}$ a dlhšej s hmotnosťou $m_2 = \SI{0.6}{\kilo\gram}$ a dĺžkou $l_2 = \SI{1.7}{\metre}$. Dĺžku $l_2$ budeme zároveň považovať aj za výšku, v ktorej sa nachádza Majovo čelo. Moment zotrvačnosti hrablí teda je \[ I_\text{hrable} = \frac{1}{3}\bigl(m_1l_1^2 + m_2 l_2^2\bigr) = \frac{1}{3}\bigl(\num{0,005} + \num{1,734}\bigr)\si[per-mode = reciprocal]{\kilo\gram\meter\squared} \doteq \SI{0.58}{\kilo\gram\meter\squared}. \] Vidíme, že príspevok za kratšiu tyč by sme mohli pokojne zanedbať. Popravde, keď ho vôbec neuvažujeme a výsledok zaokrúhlime na 2 desatinné miesta, dostávame tú istú hodnotu: $I = \SI{0.58}{\kilo\gram\meter\squared}$.
Ekvivalentom zrýchlenia $\vec{a}$ je uhlové zrýchlenie $\vec{\epsilon}$. Prirodzene, uhlové zrýchlenie nám hovorí, ako rýchlo sa mení uhlová rýchlosť $\frac{\Delta \phi}{\Delta t} = \vec{\omega} = \frac{\vec{r}\times\vec{v}}{r^2}$ v čase: \[ \vec{\epsilon} = \frac{\Delta \vec{\omega}}{\Delta t}. \]

Na hrable budú pôsobiť 3 sily. $\vec{F}_1$ – tiažová sila kovovej časti hrablí pôsobiaca v jej ťažisku, $\vec{F}_2$ – tiažová sila drevenej časti opäť pôsobiaca v jej ťažisku a $\vec{F}_\text{M}$ – sila, ktorou na hrable pôsobí Majo pri dostupovaní.

Sú len 3 možnosti, odkiaľ môžu pochádzať príspevky k sile $\vec{F}_\text{M}$.

Prvá možnosť sa týka zmeny hybnosti Majovej nohy. Hrable Majovi totiž bránia v tom, aby položil nohu prirodzene dopredu. Avšak uhol, pod ktorým Majo vtedy na hrable pôsobí, by mal tendenciu skôr otáčať drevenú tyč smerom do zeme než ju zdvíhať. Táto energia sa teda v podstate stratí, keďže s rotáciou hrablí nemá nič spoločné.
Kráčanie je vo všeobecnosti veľmi komplikovaný proces. Zoberme si napríklad naše ťažisko. To sa nepohybuje úplne vodorovne, ale skôr po akejsi jemnej sínusoide. Podobne tiež pri chôdzi presúvame váhu zboka na bok a taktiež zrýchľujeme a spomaľujeme naše končatiny. Na niektoré takéto zmeny pohybu potrebujeme využívať trenie so zemou. Pri chôdzi teda nepôsobíme výlučne iba smerom dole, ale aj trochu smerom dozadu. Týmto sa vyhýbame problému, že keď na ležiace hrable pôsobíme čisto vertikálnym smerom, tak ich nemáme šancu zrotovať. Budeme ale predpokladať, že to nie je príliš veľká sila a preto uhol $\phi$ (viď Obr. sily ) do takej miery, ako to bude možné, zanedbáme.
Tretia, najočividnejšia a najdôležitejšia možnosť, je tiažová sila. Táto sila bude samozrejme smerovať kolmo na zem a napriek tomu, že sa môže meniť od nuly po celú Majovu hmotnosť, prisúdime jej konštantnú veľkosť polovice Majovej tiaže. Čiže \[ \vec{F}_\text{M} = \frac{m_\text{M}\vec{g}}{\num{2}}. \]

V podstate sme teda celý proces spravili ekvivalentný s prípadom, kde kratšiu časť hrablí pritlačí k zemi závažie (hmotný bod) s hmotnosťou $\frac{m_\text{M}}{\num{2}}$, ktoré bude po celú dobu umiestnené na jej konci. Vďaka tomu teraz môžeme získať výsledok dvoma spôsobmi: cez sily (dynamiku) a zo zákona zachovania energie.

Dynamika - hrubý odhad

Pre jednoduchosť poďme ignorovať tiaž kratšej časti hrablí $F_1 = m_1g = \SI{5}{\newton}$.³ Do úvahy bude teda prichádzať len sila $\vec{F}_\text{M}$, ktorá sa bude usilovať o to, aby hrable Majovi vrazili do čela a sila $F_2 = m_2g = \SI{6}{\newton}$, ⁴ ktorá ju v tom bude trošku brzdiť. Pozrime sa teraz na silu $\vec{F}_\text{M}$. Ak závažie nepovažujeme za súčasť hrablí, tak $\vec{F}_\text{M} = \frac{1}{2}m_\text{M}(\vec{g}-\vec{a})$, kde $\vec{a} = \vec{\epsilon}\times\vec{l}_1$ je zrýchlenie konca kratšej časti hrablí a zároveň závažia. Teraz využijeme, že závažie je bodové. Vďaka tomu ho môžeme zobrať ako súčasť systému tak, že ho započítame do momentu zotrvačnosti: \[ I_\text{systém} = I_\text{hrable} + \frac{m_\text{M}}{2}l_1^2 = \SI{0.58}{\kilo\gram\metre\squared} + \SI{0.35}{\kilo\gram\metre\squared} = \SI{0.93}{\kilo\gram\metre\squared}. \] Tento krok (závažie je už súčasťou systému) nám umožnil používať $\vec{F}_\text{M} = \frac{m_\text{M}}{2}\vec{g}$. ⁵ Takže veľkosť momentu sily $\vec{M} = \vec{M}_\text{M} + \vec{M}_2$ bude \[ M = \frac{g}{2}\cdot \left( m_\text{M}l_1 \sin\alpha - m_2 l_2 \cos\alpha\right). \] a veľkosť uhlového zrýchlenia $\vec{\epsilon}$ \[ \epsilon(\alpha) = \frac{M}{I_\text{systém}} = \frac{g}{2} \cdot\frac{m_\text{M}\cdot l_1 \sin\alpha - m_2 l_2 \cos\alpha}{\SI{0.93}{\kilo\gram\metre\squared}}, \] \[ \epsilon(\alpha) = \left(\num{37.63}\sin\alpha - \num{5,48}\cos\alpha\right)\si[per-mode = reciprocal]{\per\second\squared}. \]

Všimnime si, že uhlové zrýchlenie závisí od uhla $\alpha$. My sme sa však s iným ako konštantným zrýchlením ešte nestretli. Zaujíma nás však len hrubý odhad. Preto si pre jednoduchosť $\epsilon$ konštantným spravme. Najrozumnejšie bude nahradiť ho jeho strednou (priemernou) hodnotou. Nekonštantnými prvkami sú len faktory $\sin\alpha$ a $\cos\alpha$. $\sin\alpha$ sa na intervale $\alpha \in \left[0,\frac{\pi}{2}\right]$ mení od $0$ po $1$ a $\cos\alpha$ od $1$ po $0$. Hrubo odhadnime strednú hodnotu týchto funkcií na danom intervale jednou polovicou⁶. Čiže zoberieme $\langle\sin\alpha\rangle = \langle\cos\alpha\rangle = \frac{1}{2}$ a teda \[ \epsilon = \frac{1}{2}\left(\num{37.63}\sin\alpha - \num{5,48}\cos\alpha\right)\si[per-mode = reciprocal]{\per\second\squared}= \SI[per-mode = reciprocal]{16.075}{\per\second\squared}. \]

Vieme, ako sa mení uhlová rýchlosť $\vec{\omega}$ a prejdený uhol v radiánoch $\vec{\alpha}$ v čase pri konštantnom uhlovom zrýchlení $\vec{\epsilon}$: \[ \vec{\omega}(t) = \vec{\omega}_0 + \vec{\epsilon}\cdot t, \] \[ \vec{\alpha}(t) = \vec{\alpha}_0 + \vec{\omega_0}t + \frac{1}{2}\vec{\epsilon}\cdot t^2. \] V našom prípade $\vec{\alpha}_0 = 0$, $\vec{\omega}_0 = \SI[per-mode = reciprocal]{0}{\per\second}$. Chceme získať rýchlosť konca hrablí (vo vzdialenosti $\SI{1.7}{\metre}$): \[ v(t) = \omega(t)\cdot\SI{1.7}{\metre} = \epsilon\cdot t\cdot\SI{1.7}{\metre}, \] keď $\alpha = \frac{\pi}{2}$. Správny čas získame zo vzťahu pre prejdený uhol: \[ \frac{\pi}{2} = \frac{1}{2}\epsilon t^2.\] \[ t = \sqrt{\frac{\pi}{\epsilon}} = \SI{0.44}{\second}. \] A teda \[ v(t) \doteq \SI[per-mode = reciprocal]{12}{\metre\per\second} \doteq \SI[per-mode = reciprocal]{43.3}{\kilo\metre\per\hour}. \] Od vás nám plne stačili len takéto rýchle, hrubé odhady. Poďme to však teraz zrátať presnejšie, nech si overíme, či sme sa trafili.

Dynamika – presnejšie

Vráťme do hry už aj tiaž kratšej časti hrablí. Veľkosť momentu sily $\vec{M} = \vec{M}_\text{M} + \vec{M}_1 + \vec{M}_2$, bude v tomto prípade \[ M = \frac{g}{2}\cdot \bigl( \left(m_1 + m_\text{M}\right)l_1 \sin\alpha - m_2 l_2 \cos\alpha\bigr). \] Veľkosť uhlového zrýchlenia $\vec{\epsilon}(\alpha)$ zas \[ \epsilon = \frac{M}{I_\text{systém}} = \frac{g}{2} \cdot\frac{(m_1 + m_\text{M})\cdot l_1 \sin\alpha - m_2 l_2 \cos\alpha}{\SI{0.93}{\kilo\gram\metre\squared}}, \] \[ \epsilon = \left(\num{37.9}\sin\alpha - \num{5.48}\cos\alpha\right)\si[per-mode = reciprocal]{\per\second\squared}. \]

Ako sme už spomínali, uhlové zrýchlenie závisí netriviálne od uhla $\alpha$. Čo iné, než zobrať priemernú hodnotu, by sme s aparátom, ktorý poznáme, vedeli spraviť? Môžeme čas rozbiť na nejaké malé časové úseky $\Delta t$ a skúsiť predpokladať, že zrýchlenie sa počas týchto časových úsekov nemení.⁷ Konkrétne, problém nasimulujeme nasledujúcim spôsobom. Pre každý časový úsek si zaktualizujeme uhlovú rýchlosť a uhlové zrýchlenie a následne sa posunieme o uhol, ktorý s danou rýchlosťou a zrýchlením ľubovoľný bod hrablí za $\Delta t$ prejde. Proces opakujeme, kým prejdený uhol neprekročí $\ang{90} = \frac{\pi}{2}$. Rýchlosť, ktorou hrable zasiahnu Maja do čela bude $v = \omega\cdot\SI{1.7}{\metre}$, kde $\omega$ je správne zaktualizovaná. Avšak predtým, než predstavím možný kód pre takúto simuláciu, vykreslime si ešte, ako tá závislosť $\epsilon(\alpha)$ vyzerá (Obr. epsilon ).

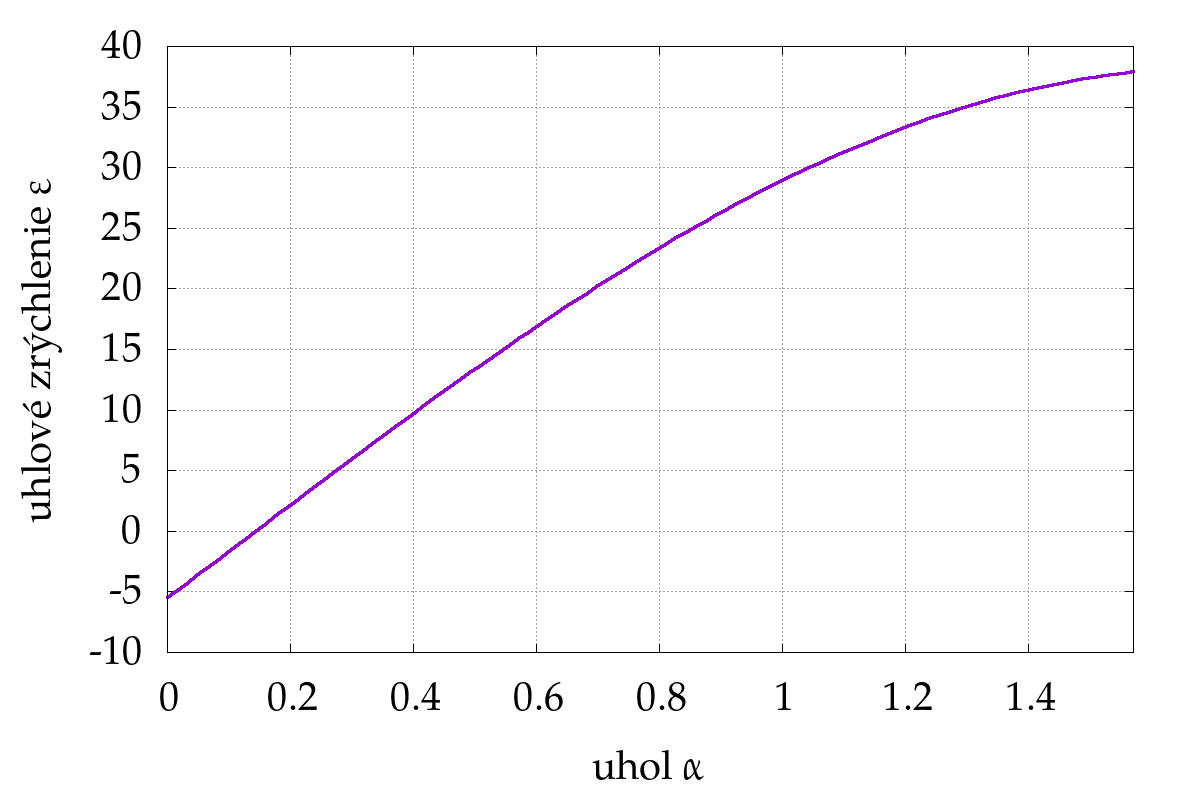
Závislosť uhlového zrýchlenia $\epsilon$ od uhla $\alpha$ pri $\phi = 0$.

Všimnime si, že pre malé uhly je $\epsilon$ záporné. To nechceme. Vôbec to totiž nepopisuje situáciu, ktorú pozorujeme. Podľa daného grafu, by sme hrable z horizontálnej polohy ($\alpha = 0$) nikdy nezdvihli – na zdvihnutie by zrýchlenie muselo byť kladné už pre $\alpha = 0$. Majo teda naozaj musí pôsobiť na hrable aj smerom dozadu – príspevok k sile $\vec{F}_\text{M}$ z bodu 2, označme ho $\vec{F}_{\text{M}_\text{hor}}$, teda nemôžeme zanedbať úplne. Vyjadrime si jeho príspevok k uhlovému zrýchleniu: \[ \epsilon_{\text{M}_\text{hor}} = \frac{M_{\text{M}_\text{hor}}}{I_\text{systém}} = \frac{l_1\cdot F_{\text{M}_\text{hor}}\cdot\cos\alpha}{I_\text{systém}}. \] Je zrejmé, že na to, aby sme docielili kladné uhlové zrýchlenie od začiatku, $\epsilon_{\text{M}_\text{hor}}(\alpha = 0)$ musí byť väčšie ako $\SI[per-mode = reciprocal]{5.48}{\per\second\squared}$. Zoberme teda napríklad $\epsilon_{\text{M}_\text{hor}}(\alpha = 0) = \SI[per-mode = reciprocal]{5.49}{\per\second\squared}$, čo zodpovedá sile $F_{\text{M}_\text{hor}} = \SI[per-mode = reciprocal]{51.06}{\newton}$. Pre jednoduchosť predpokladajme, že sila $\vec{F}_{\text{M}_\text{hor}}$ bude po celú dobu konštantná. Nový vzťah pre uhlové zrýchlenie teda bude: \[ \epsilon = \left(\num{37.9}\sin\alpha + \num{0.01}\cos\alpha\right)\si[per-mode = reciprocal]{\per\second\squared}. \]

Kód v pythone by mohol vyzerať napríklad takto:

from math import cos, sin, pi

def epsilon(alpha):
    return 37.9*sin(alpha) + 0.01*cos(alpha)

delta_t = 0.00001

alpha = 0
omega = 0
while alpha < pi/2:
    zrychlenie = epsilon(alpha)
    alpha += omega*delta_t + (zrychlenie*delta_t**2)/2
    omega += zrychlenie*delta_t
print(omega*1.7)

Výsledok pre $\Delta t = \SI{e-5}{\second}$ je \[ v = \SI[per-mode = reciprocal]{14.8}{\metre\per\second} \doteq \SI[per-mode = reciprocal]{53.28}{\kilo\metre\per\hour}. \] Pre kontrolu či časový úsek $\Delta t = \SI{e-5}{\second}$ je vhodná voľba, skontrolujme, či o rád menší a o rád väčší časový úsek dajú podobné výsledky. $\Delta t = \SI{e-4}{\second}$ dáva $v = \SI[per-mode = reciprocal]{14.806}{\metre\per\second}$ a pre $\Delta t = \SI{e-6}{\second}$ je $v = \SI[per-mode = reciprocal]{14.803}{\metre\per\second}$.

Zákon zachovania energie

Potenciálna energia bodového závažia a kovovej časti hrablí sa premení na prírastok potenciálnej energie drevenej tyče, rotačnú kinetickú energiu hrablí a kinetickú energiu bodového závažia: \[ \frac{m_\text{M}}{2} g l_1 + m_1 g \frac{l_1}{2} = m_2 g \frac{l_2}{2} + \frac{1}{2} I_\text{hrable} \omega^2 + \frac{1}{2} \frac{m_\text{M}}{2} l_1^2 \omega^2. \] Nás zaujíma, akou rýchlosťou zasiahnu hrable Majovo čelo. Túto rýchlosť môžeme vyjadriť ako \[ v = \omega\cdot\SI{1.7}{\metre}. \] Po vyjadrení veľkosti uhlovej rýchlosti $\omega$ zo zákona zachovania energie dostávame \[ v = \sqrt{\frac{m_\text{M} g l_1 + m_1 g l_1 - m_2 g l_2}{I_\text{hrable} + \frac{1}{2}m_\text{M}l_1^2}}\cdot\SI{1.7}{\metre}, \] \[ v \doteq \SI[per-mode = reciprocal]{13.69}{\metre\per\second} \doteq \SI[per-mode = reciprocal]{49.28}{\kilo\metre\per\hour}. \]

Záver

V porovnaní s riešením cez energie, hrubým odhadom sme sa dopustili chyby $\SI[per-mode = reciprocal]{1.69}{\metre\per\second} = \SI[per-mode = reciprocal]{6.084}{\kilo\metre\per\hour}$. Keby sme použili presnú strednú hodnotu $\langle\sin\alpha\rangle = \langle\cos\alpha\rangle = \num{0.637}$, dostali by sme $v = \SI[per-mode = reciprocal]{13.58}{\metre\per\second} = \SI[per-mode = reciprocal]{48.89}{\kilo\metre\per\hour}$ a teda chybu $\SI[per-mode = reciprocal]{0.11}{\metre\per\second} = \SI[per-mode = reciprocal]{0.396}{\kilo\metre\per\hour}$. To vôbec nie je zlé! Horizontálna sila, ktorú sme pridali pri presnejšom riešení cez sily, pridala zhruba $\SI[per-mode = reciprocal]{1.11}{\metre\per\second} \doteq \SI[per-mode = reciprocal]{4}{\kilo\metre\per\hour}$. Zarátanie vplyvu kratšej časti hrablí zas zhruba $\SI[per-mode = reciprocal]{0.06}{\metre\per\second} \doteq \SI[per-mode = reciprocal]{0.2}{\kilo\metre\per\hour}$.

Skutočná dynamika ale môže výrazne závisieť aj od toho, ktorou časťou nohy na hrable dopadneme – ak napríklad dopadneme na hrable tak, že pätu ešte nemáme položenú na zemi, je dosť možné, že nohu reflexívne potiahneme dozadu, kým sa päta zeme nedotkne.⁸ Tým by tá horizontálna zložka sily mohla spraviť výraznejší rozdiel. Rovnako, ako dostupujeme, čím ďalej tým viac sa na nohu zavažujeme. Na druhú stranu, kým máme nohu vyvýšenú, ťažšie sa na ňu prenáša váha. Polovica Majovej hmotnosti je teda naozaj hrubý odhad. Celkovo však odhadujeme, že hrable Maja zasiahnú rýchlosťou okolo $\SI[per-mode = reciprocal]{50}{\kilo\metre\per\hour}$, čo musí dosť bolieť.

Budeme používať notáciu, kde vektorové veličiny bez šípky navrchu (napr. $\vec{F}\to F$) značia veľkosť.↩︎
U kratšej časti budeme pre jednoduchosť ignorovať, že je v skutočnosti súčtom dlhších zubov a kratších ‘medzizubových spojív’ a pre účely určenia momentu zotrvačnosti si ju predstavíme ako kovový obdĺžnik, ktorý je už len súčtom pásikov (tyčí) zubovej dĺžky. Ak si obdĺžnik rozdelíme na $n$ totožných tenkých pásikov (os otáčania prechádza spodnou hranou tohto obdĺžnika), tak $I = n\cdot\left(\frac{1}{3}\frac{m_1}{n}l_1^2\right) = \frac{1}{3}m_1l_1^2$, čo je rovnaký výsledok¸ aký by sme dostali pre tenkú tyč s dĺžkou $l_1$ a hmotnosťou $m_1$.↩︎
Nakoľko je zanedbateľná v porovnaní so silou od Maja a tiež príslušný moment sily $\vec{M}_1$ má hodnotu len $\SI{0.5}{\newton\meter}$.↩︎
Veľkosťou je táto sila podobná tej, ktorú zanedbávame, tu je však už veľkosť momentu sily $M = \SI{5.2}{\newton\meter}$.↩︎
Nadštandardné (nelámte si týmto príliš hlavu) výpočtové znázornenie ekvivalencie týchto dvoch možností. Začneme so silou $\vec{F}_\text{M} = \frac{1}{2}m_\text{M}(\vec{g}-\vec{\epsilon}\times\vec{l}_1)$ v kombinácii s momentom zotrvačnosti hrablí bez bodového závažia ($I_\text{hrable}$) a úpravami sa dostaneme k bodovému závažiu započítanému do momentu zotrvačnosti ($I_\text{systém}$) a sile $\vec{F}_\text{M} = \frac{1}{2}m_\text{M}\vec{g}$. \[I_\text{hrable}\vec{\epsilon} = \vec{M}_\text{M} + \vec{M}_2 = \vec{l}_1\times \vec{F}_\text{M} + \vec{M}_2 = \frac{m_\text{M}}{2}\cdot\bigl(\vec{l}_1\times\vec{g} - \vec{l}_1\times(\vec{\epsilon}\times\vec{l}_1)\bigr) + \vec{M}_2,\] \[I_\text{hrable}\vec{\epsilon}+\frac{m_\text{M}}{2}\vec{l}_1\times(\vec{\epsilon}\times\vec{l}_1) = \frac{m_\text{M}}{2}\vec{l}_1\times\vec{g} + \vec{M}_2. \] Teraz využijeme identitu: $\vec{a}\times(\vec{b}\times\vec{c}) = (\vec{a}\cdot\vec{c})\vec{b} - (\vec{a}\cdot\vec{b})\vec{c}$. V našom prípade $\vec{l}_1\times(\vec{\epsilon}\times\vec{l}_1) = (\vec{l}_1\cdot\vec{l}_1)\vec{\epsilon} - (\vec{l}_1\cdot\vec{\epsilon})\vec{l}_1 = l_1^2\vec{\epsilon}$. Čiže: \[I_\text{systém}\vec{\epsilon} = (I_\text{hrable}+\frac{m_\text{M}}{2}l_1^2)\vec{\epsilon} = \vec{l}_1\times\frac{m_\text{M}}{2}\vec{g} + \vec{M}_2.\]↩︎
Skutočná stredná hodnota (zaokrúhlená na $3$ desatinné miesta) je $\num{0.637}$.↩︎
Konštantné časové úseky $\Delta t$ by sme mohli vymeniť za konštantné uhlové úseky $\Delta \alpha$ tým, že by sme vzali \[ \Delta t (\alpha) = \frac{-\omega(\alpha) + \sqrt{\omega^2(\alpha) + 2\cdot\Delta\alpha\cdot\epsilon(\alpha)}}{\epsilon(\alpha)}. \] Získali by sme tým napríklad istotu, že výslednú rýchlosť máme pre $\alpha = \ang{90}$. Ak ale zoberieme $\Delta t$ dostatočne malé, výrazný rozdiel by to spraviť nemalo. Skúsila som oba spôsoby simulácie a rozdiel bol až na treťom desatinnom mieste.↩︎
Presnejšie odhady by sa dali spraviť experimentálne.↩︎

Diskusia

Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.

Pre pridávanie komentárov sa musíš prihlásiť.

2. Čo ti hrabe? vzorové riešenie