2. Meranie trenia vzorové riešenie

Zadanie

Majo vymyslel nový spôsob, ako merať šmykové trenie medzi briežkom pred svojím domom a svojím obľúbeným hmotným bodom s hmotnosťou \(m\). Briežok má tvar naklonenej roviny so sklonom \(\alpha\) a je nasledovaný rovinkou. Majo položí hmotný bod na briežok do výšky \(h\). Potom ho pustí a hmotný bod sa zošmykne tak, že zastane vo vodorovnej vzdialenosti \(l\) od miesta, kam ho položil. Teraz by z týchto údajov chcel určiť koeficient šmykového trenia \(f\) medzi bodom a briežkom. Trenie medzi bodom a briežkom je rovnaké, ako medzi bodom a rovinkou. Určite z týchto údajov aj Vy, aký by mal byť tento koeficient.

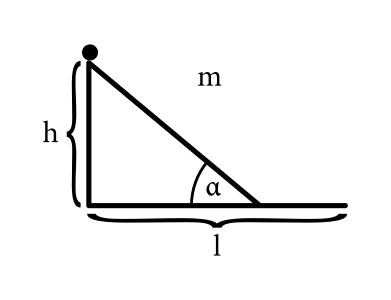
Môžete predpokladať, že bod prejde spojom medzi briežkom a rovinkou bez akéhokoľvek narazenia, t. j. stále sa hýbe po povrchu zeme.

Na úvod sa zamyslime, prečo by sa hmotný bod umiestnený na vrchu briežka mal začať pohybovať. Pozrime sa, aké sily naň pôsobia. Pôsobí naň tiažová sila \(F_G = mg\). Tá sa dá rozložiť na dve zložky. Rozkladá sa na tlakovú zložku \(F_T = m g \cos \alpha\), ktorá pôsobí v smere kolmom na briežok, a na pohybovú zložku \(F_{p}=mg \sin\alpha\), ktorá pôsobí v smere rovnobežnom s briežkom.

Keďže hmotný bod pôsobí nejakou tlakovou silou na briežok, zo zákona akcie a reakcie vieme povedať, že aj briežok musí pôsobiť na hmotný bod rovnako veľkou, ale opačnou normálovou silou \(F_{N}=mg \cos\alpha\). Z toho ale máme, že trecia sila, ktorá bráni hmotnému bodu v pohybe, má veľkosť najviac \(F_{t} \leq fF_{N} = mgf \cos\alpha\). Ak ale platí, že pohybová zložka tiažovej sily \(F_{p}\) je menšia, ako táto trecia sila, Majov hmotný bod sa nikdy nepohne. Vtedy platí \[ \begin{aligned} F_{p} &\leq F_{t} \\ mg \sin \alpha &\leq mg\,f \cos\alpha, \\ f &\geq \tan\alpha \\ \end{aligned} \]

Ak teda platí, že koeficient šmykového trenia \(f\) je aspoň \(\tan\alpha\), Majov hmotný bod sa nepohne. To ale znamená, že v tomto prípade Majo nevie presne určiť, akú hodnotu má koeficient šmykového trenia \(f\).

Ako je to ale v prípade, že \(f < \tan\alpha\)? V tom prípade je výsledná sila, ktorá pôsobí na Majov hmotný bod v smere pohybu, nenulová. Keďže rozdiel týchto síl nezávisí od polohy hmotného bodu na briežku, na hmotný bod bude v každom bode jeho pohybu po briežku pôsobiť sila s nenulovou veľkosťou v smere jeho pohybu. Takže určite nezastaví na briežku, ale niekde na rovinke.

Zamyslime sa, aké sily pôsobia na hmotný bod na rovinke. Stále pôsobí tiažová sila \(F_{G}=mg\). Tá ale teraz celá zodpovedá tlakovej zložke \(F_{T}\)¹, a teda čo do veľkosti aj normálovej sile \(F_{N}\). Na hmotný bod tak pôsobí trecia sila s veľkosťou \(F_{t}=mgf\), ktorá pôsobí proti smeru pohybu hmotného bodu. V tomto prípade ale nemáme pohybovú zložku tiažovej sily, ktorá by pôsobila na hmotný bod, a tak je trecia sila jediná, ktorá má vplyv na to, ako sa bude hmotný bod pohybovať. A keďže je jej veľkosť nenulová, hmotný bod niekedy určite zastať musí.

Keď už sme sa zamysleli kvalitatívne nad tým, čo sa v tejto situácii deje, poďme všetko vyjadriť kvantitatívne. Prípad, kedy by bolo \(f \geq \tan\alpha\) sme už vyriešili, a tak riešme už iba to, čo sa stane, ak \(f < \tan\alpha\). V tomto prípade hmotný bod zastaví niekde na rovinke. Ak si túto výšku zvolíme ako hladinu nulovej výšky (a teda aj nulovej potenciálnej energie), potenciálna energia hmotného bodu na vrchole briežka musela byť \(E_{p} = mgh\). V tomto momente sa hmotný bod nehýbal, a teda mal nulovú kinetickú energiu. Jeho celková mechanická energia \(E\) tak na začiatku bola rovná jeho potenciálnej energii \(E_{p}\). Na konci je bod na rovinke, takže má nulovú potenciálnu energiu. Navyše sa nehýbe, čiže má nulovú kinetickú energiu. Mechanická energia tohto bodu na konci je teda nulová. To znamená, že v priebehu svojho pohybu musel stratiť energiu \(E = E_{p}\).

Hmotný bod mohol stratiť svoju energiu iba pri tom, ako konal prácu, prípadne ju získať, ak by na ňom bola konaná nejaká práca. Prácu na hmotnom bode konala iba tiažová sila, a to na dráhe \(h\) (lebo hmotný bod prekonal výškový rozdiel \(h\)). To ale v skutočnosti zodpovedá tomu, že na začiatku mal potenciálnu energiu \(E_{p}=mgh\). Túto energiu už máme zahrnutú v našich myšlienkach. Na druhej strane strácal hmotný bod svoju energiu tak, že musel prekonávať treciu silu. V danom okamihu síce trecia sila pôsobila na hmotný bod, ale zo zákona akcie aj reakcie musel aj hmotný bod pôsobiť silou na podložku. A keďže touto silou pôsobil na nejakej dráhe, konal prácu, a teda strácal energiu.

Takto strácal energiu na dvoch úsekoch – na briežku a na rovinke. Keď bol na briežku, mala trecia sila (a teda aj reakčná sila) veľkosť \(F_{t}=mgf \cos\alpha\) a táto sila pôsobila na dráhe \(s=\frac{h}{\sin\alpha}\). Takže hmotný bod na tomto úseku stratil energiu \[ E_1 = mgfh \frac{\cos\alpha}{\sin\alpha} = mgfh \cot\alpha. \]

Na rovinke mala trecia sila veľkosť \(F_{t}=mgf\) a pôsobila na dráhe \(s=l-h \cot\alpha\) (táto dráha je kladná, a teda má zmysel iba vtedy ak \(l > h \cot\alpha\), čiže ak \(\frac{h}{l} < \tan\alpha\)). Na tejto časti tak hmotný bod stratil energiu \[ E_{2} = mgf \left(l - h \cot\alpha\right) = mgfl - mgfh \cot\alpha. \]

Celková strata energie hmotného bodu teda je \[ E = E_1 + E_2 = mgfh \cot\alpha + mgfl - mgfh \cot\alpha = mgfl\]

Vieme, že táto strata energie sa má rovnať potenciálnej energii na začiatku, a teda má platiť \[ mgh = mgfl. \]

Odtiaľ už jednoducho vyjadríme veľkosť \(f\) (všimnime si, že vďaka podmienke \(\frac{h}{l} < \tan\alpha\) sme stále v prípade \(f < \tan\alpha\)) \[ f=\frac{h}{l}. \]

Tým sme zistili, že ak pre koeficient šmykového trenia \(f\) platí \(f < \tan\alpha\), vieme ho vypočítať ako \(f=\frac{h}{l}\), a že inak ho zo zadaných informácií vypočítať nevieme.