7. Model slnečnej sústavy vzorové riešenie

Zadanie

Terka si chcela zútulniť svoju novú izbu. Rozhodla sa vyrobiť si model slnečnej sústavy, ktorý si zavesí nad posteľ. Keďže najguľatejšia vec, čo mala poruke, bolo koleso polomeru \(r\), začala s ním. Pripevnila ho na koniec tyče dĺžky \(R\). A hotovo! Aspoň zatiaľ. Koniec tejto tyče voľne upevnila vo výške \(r\) nad zemou. A roztočila koleso rýchlosťou \(\omega\). To začalo obiehať bez prešmykovania okolo bodu upevnenia. Aká je jeho kinetická energia, ak viete, že hmotnosť obruče kolesa je \(m\), a hmotnosti špicí a osí sú zanedbateľné?

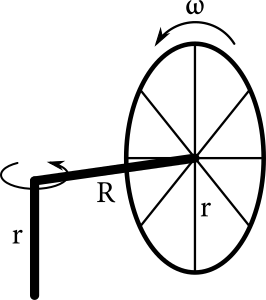
Táto úloha na prvý pohľad nevyzerala veľmi vábne, no v skutočnosti to vôbec nebolo také bolestivé. Ako prvé si uvedomíme, že forma kinetickej energie bude v tomto prípade rotačná, ktorú vypočítame ako \(\frac{1}{2}I\omega^2\), kde \(I\) je moment zotrvačnosti telesa vzhľadom na nejakú os a \(\omega\) je uhlová rýchlosť okolo tejto osi. Máme tu dva rotačné pohyby: jeden očividný, a to otáčanie kolesa okolo vlastnej osi uhlovou rýchlosťou \(\omega\) a druhý pozostáva z otáčania tyče dĺžky \(R\) spolu s kolesom okolo tyče dĺžky \(r\). Zo zadania vieme, že počas druhého pohybu sa koleso otáča po zemi bez prešmykovania, a teda jeho translačná rýchlosť \(v_t\) je rovnaká ako obvodová \(v_o\): \[ v_o =\omega r = v_t. \]

Ďalej si musíme uvedomiť, že translačná rýchlosť kolesa je vlastne obvodová rýchlosť točiacej sa tyče dĺžky \(R\). Z toho vyplýva, že jej uhlová rýchlosť, nazvime ju \(\Omega\), bude \[ \Omega = \frac{v_t}{R} = \frac{\omega r}{R}. \]

Keď už sme si vyjasnili rýchlosti, poďme sa pozrieť na to druhé – moment zotrvačnosti. Zaznačme si do obrázka tri osi, na ktoré sa budeme odkazovať.

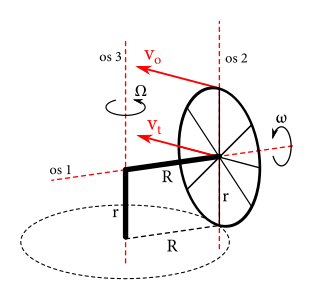
Prvá prechádza stredom kolesa, druhá je kolmá na tyč dĺžky \(R\) a prechádza rovinou kolesa a tretia je predĺžením tyče dĺžky \(r\). Vybavme najskôr prvý otáčavý pohyb, teda točenie kolesa okolo osi 1. Keďže naše koleso má hmotnosť \(m\) so zanedbateľnými priečkami, každý element jeho hmotnosti je rovnako vzdialený od osi \(1\) a to presne polomer \(r\). Jeho moment zotrvačnosti bude jednoducho \(I_1 = mr^2\). Keď to skombinujeme s tým, že okolo osi \(1\) sa koleso točí uhlovou rýchlosťou \(\omega\), získame prvú časť výsledku, a teda že rotačná energia tohto pohybu je \[ E_{r1} = \frac{1}{2}I_1\omega^2 = \frac{1}{2}mr^2\omega^2. \]

Ako sme vraveli, druhá časť rotačnej energie bude pochádzať z pohybu okolo osi \(3\), kde rýchlosť točenia je \(\Omega\). Aký je však moment zotrvačnosti kolesa vzhľadom na túto os? Na to použijeme Steinerovu vetu, ktorá vraví, že ak poznáme moment zotrvačnosti telesa \(I_0\) vzhľadom na os prechádzajúcu jeho ťažiskom a chcem vypočítať moment zotrvačnosti \(I\) okolo rovnobežnej osi neprechádzajúcej ťažiskom vzdialenú \(d\) od prvej osi, platí \(I=I_0+md^2\).

To znamená, že by bolo pre nás výhodné, keby sme poznali moment zotrvačnosti kolesa vzhľadom na os \(2\), lebo potom by sme si ten okolo osi \(3\) mohli jednoducho dopočítať. To nie je žiadny problém, lebo moment zotrvačnosti kolesa vzhľadom na os \(2\) v rovine kolesa prechádzajúcu jeho ťažiskom je ľahko nájditeľný na internete (pre integrovania nechtivých), a je \(I_2=\frac{1}{2}mr^2\). Moment zotrvačnosti kolesa vzhľadom na os \(3\) bude podľa Steinerovej vety \[ I_3 = I_2 + mR^2 = \frac{1}{2}mr^2 + mR^2 = m\left(\frac{r^2}{2} + R^2\right). \]

Toto bol posledný kúsok skladačky. Vieme, že okolo osi \(3\) obieha koleso uhlovou rýchlosťou \(\Omega\), a že tyč dĺžky R je nehmotná, a teda môžeme vypočítať druhú časť rotačnej energie \[ E_{r2} = \frac{1}{2} I_3\Omega^2 = \frac{1}{2}m\left(\frac{r^2}{2} + R^2\right)\Omega^2 = \frac{1}{2}m \left(\frac{r^2}{2} + R^2\right)\left(\frac{\omega r}{R}\right)^2 = \frac{1}{2}m\left(\frac{\omega r^4}{2R}+\omega^2r^2\right). \]

Ostáva nám už len spokojne tieto energie sčítať a radovať sa \[ E = E_{r1} + E_{r2} = \frac{1}{2}mr^2\omega^2 + \frac{1}{2}m\left(\frac{\omega r^4}{2R} + \omega^2r^2\right) = \frac{1}{2} mr^2 \omega^2\left(\frac{r^2}{2R} + 2\right). \]