5. Presun eráru vzorové riešenie

Zadanie

Zvyčajne sa v zadaniach fyzikálnych príkladov pod pojmom pružina chápe mierne zidealizovaná vec z reálneho sveta. Konkrétne taká, ktorá po natiahnutí z pokoja o \(x\) ťahá späť silou priamo úmernou predĺženiu, t.j. \(F=-kx\), kde kladná konštanta \(k\) je zvaná tuhosťou pružiny. Inak tomu nie je ani tu.

Pri veľkom letnom presune eráru z už spomínanej miestnosti F1-229 do miestnosti T2¹ si Krtko v skrini s dokonalými fyzikálnymi pomôckami všimol päť rovnakých pružín. Chvíľu sa s nimi hral a pospájal ich tak, že medzi dve z nich sériovo pripevnil paralelne spojenú zvyšnú trojicu. Potom zmeral tuhosť a zamyslel sa. Po chvíli vyrátal rovnakú tuhosť a spokojne odložil pružiny nazad do skrine. Aká je tuhosť takejto konštrukcie?

---

1. miestnosť Korešpondenčného Seminára z Programovania↩︎

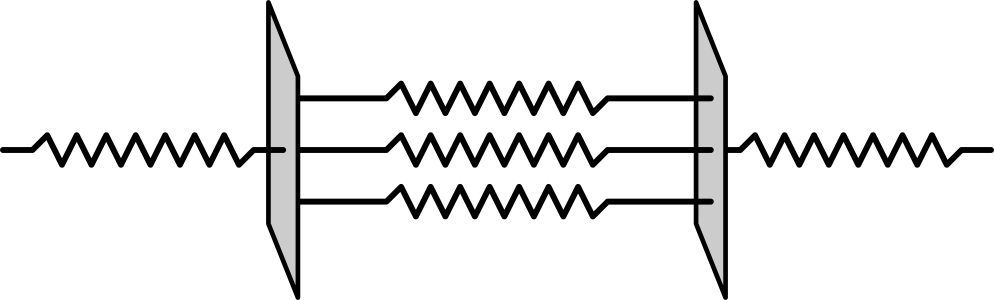
Tuhosť pružiny je naozaj veľmi jednoduchý koncept. Už jej jednotka \(\si{\newton\per\metre}\) nám napovedá, že pôjde o silu, ktorou by sme mali ťahať, aby sme pružinu predĺžili o \(\SI{1}{\metre}\). Poďme sa pozrieť, ako sa budú pružinky správať pri ich sériovom a paralelnom zapojení!

Vieme, že tuhosť \(k\) vyjadríme ako \(\frac{F}{x}\), kde \(F\) je sila a \(x\) predĺženie.

Ak zapojíme za seba, teda sériovo \(n\) pružiniek s tuhosťou \(k_1, k_2, \ldots, k_n\) za seba, novú tuhosť nazvúc \(k_s\), vieme, že pri rovnakej sile (na všetky skutočne pôsobím rovnakou silou) sa nám \(i\)-ta z nich predĺži o \(\frac{F}{k_i}\), teda spolu sa predĺžia o \(F \cdot (\frac{1}{k_1}+\frac{1}{k_2}+\ldots+\frac{1}{k_n})\). Môžeme teda vyjadriť, že \(\frac{1}{k_1}+\frac{1}{k_2}+\ldots+\frac{1}{k_n} = \frac{x}{F}\), čo je ale prevrátenou hodnotou tuhosti, teda \(\frac{1}{k_s}\). Potom však vieme, že \(k_2s = \frac{1}{\frac{1}{k_1}+\frac{1}{k_2}+\ldots+\frac{1}{k_n}}\).

Pri paralelnom zapojení, teda za sebou môžeme k vyjadreniu novej tuhosti \(k_p\) vzniknuvšieho súpružinia využiť elementárne pozorovanie, že pri predĺžení o \(x\) pôsobí \(i\)-ta pružinka silou \(k_ix\). Teda v súčte vieme povedať, že \(F = k_1x+k_2x+\ldots+k_nx = (k_1+k_2+\ldots+k_n)x\). Opäť vieme úpravou dostať tvar vyjadrujúci \(\frac{F}{x}\), teda celkovú tuhosť paralelného súpružinia: \(\frac{F}{x}= k_1+k_2+\ldots+k_n = k_p\)

Naša sústava sú teda sériovo zapojené tri celky - dva razy jedna pružina a medzi tým jedno paralelné súpružinie a všetky pružinky majú tuhosť \(k\). Poďme si to teda rozpísať! \(k_c = \frac{1}{\frac{1}{k}+\frac{1}{k+k+k}+\frac{1}{k}}=\frac{1}{\frac{3+1+3}{3k}}=\frac{3}{7}k\)

Tuhosť sústavy je teda \[ k\ \si{\newton}\SI[parse-numbers = false]{\frac{7}{3}}{\metre} = \frac{3}{7} k\ \si{\newton\per\metre}. \]