6. Ja s tebou zatočím! vzorové riešenie

Začnime tým, že si odhadneme, koľko otočiek by palička urobila, ak by sa nerozpadala. Keďže palička padá voľným pádom, pád z výšky \(H\) by jej trval \(t=\sqrt{\frac{2H}{g}}\). Označme periódu otáčania paličky \(\tau\). Potom by palička vykonala \(N_{0}=\left\lfloor \frac{t}{\tau}\right\rfloor =\left\lfloor \frac{1}{\tau}\sqrt{\frac{2H}{g}}\right\rfloor\) otočiek pred dopadom. Pre numerické hodnoty zo zadania \(N_{0}=22\). Toto číslo je užitočným odhadom. Vieme totiž, že na paličku nepôsobia žiadne vonkajšie sily, preto ťažisko paličky musí poklesnúť o rovnakú výšku za daný čas bez ohľadu na to, či sa palička rozpadá alebo nie. Ak viem rozpadaním docieliť, že niektorý kúsok paličky dopadne skôr ako ťažisko, tak toto číslo slúži ako horný odhad. Ak by všetky kúsky dopadli naraz, tak je toto číslo riešením.

Poďme sa teraz pozrieť, čo sa deje pri rozpadaní paličky. Uvažujme paličku hmotnosti \(m\) a dĺžky \(l\), ktorej ťažisko sa pohybuje rýchlosťou \(u_{0}\) nadol a ktorá rotuje okolo svojho ťažiska uhlovou rýchlosťou \(\omega_{0}\) vo vertikálnej rovine. V istom momente, keď je palička práve vo vodorovnej polohe, sa táto palička rozpadne presne v strede. Nájdime, aké budú rýchlosti a uhlové rýchlosti jednotlivých polovíc paličky.

Na paličku nepôsobia žiadne vonkajšie sily ani momenty síl. Tým pádom sa zachováva hybnosť i moment hybnosti. Okrem toho pri rozpadaní palička nekoná prácu, preto platí aj zákon zachovania energie. Jednou z možností je teda napísať si ZZH, ZZMH a ZZE, čo predstavuje sústavu siedmich rovníc, a z nich vybúchať hľadané rýchlosti a uhlové rýchlosti. Alebo druhou možnosťou je zapojiť hlavu a uľačiť si život. Napríklad si môžeme uvedomiť, že translačný pohyb musí prebiehať len vo zvislom smere a rotačný pohyb len v jednej zvislej rovine danej počiatočnou rotáciou paličky. Tým sa problém zredukuje na 1D a stačí nám písať skalárne verzie ZZH a ZZMH, čím sa počet rovníc, ktoré treba riešiť, zredukuje na tri. Riešeniu danej sústavy sa však dá aj úplne vyhnúť. Teda presnejšie povedané, riešenie sa dá uhádnuť, a potom si ho vieme overiť dosadením do danej sústavy.

Začnime tým, že si napíšeme výrazy pre hybnosť, moment hybnosti a energiu pred rozpadom a po rozpade. Hybnosť (vertikálna) pred rozpadom je jednoducho \[ p_{0}=mu_{0}\text{.} \] Moment hybnosti budeme písať vzhľadom na ťažisko paličky. Tým pádom príspevok translačného pohybu k momentu hybnosti je nulový, lebo rameno hybnosti je nulové, a zostáva tak len príspevok za rotáciu \[ L_{0}=J\omega_{0}=\frac{1}{12}ml^{2}\omega_{0}\text{.} \] Energia pred rozpadom pozostáva z translačnej kinetickej energie a rotačnej kinetickej energie \[ E_{0}=\frac{1}{2}mu_{0}^{2}+\frac{1}{2}J\omega_{0}^{2}=\frac{1}{2}mu_{0}^{2}+\frac{1}{24}ml^{2}\omega_{0}^{2}\text{.} \]

Označme rýchlosti polovičiek paličky po rozpade \(u_{1}^{+}\) a \(u_{1}^{-}\) a uhlové rýchlosti \(\omega_{1}^{+}\) a \(\omega_{1}^{-}\), pričom horný index \(^{+}\) značí polovicu, ktorá odletí po rozpade nadol, a index \(^{-}\) tú, ktorá odletí nahor. Pripomeňme, že nové hmotnosti a dĺžky sú polovičné. Hybnosť po rozpade je potom \[ p_{1}=\frac{m}{2}u_{1}^{+}+\frac{m}{2}u_{1}^{-}=\frac{m}{2}\left(u_{1}^{+}+u_{1}^{-}\right)\text{.} \] Moment hybnosti píšeme opäť vzhľadom na ťažisko pôvodnej paličky. Tentoraz aj translačné zložky pohybu prispievajú k celkovému momentu hybnosti, pretože ich rameno je nenulové. Moment hybnosti po rozpade je \[\begin{eqnarray*} L_{1} & = & \frac{m}{2}u_{1}^{+}\frac{l}{4}-\frac{m}{2}u_{1}^{-}\frac{l}{4}+\frac{1}{12}\frac{m}{2}\left(\frac{l}{2}\right)^{2}\omega_{1}^{+}+\frac{1}{12}\frac{m}{2}\left(\frac{l}{2}\right)^{2}\omega_{1}^{-}=\\ & = & \frac{1}{8}ml\left(u_{1}^{+}-u_{1}^{-}\right)+\frac{1}{96}ml^{2}\left(\omega_{1}^{+}+\omega_{1}^{-}\right)\text{.} \end{eqnarray*}\] Energia po rozpade je súčtom translačnej a rotačnej kinetickej energie \[\begin{eqnarray*} E_{1} & = & \frac{1}{2}\frac{m}{2}\left(u_{1}^{+}\right)^{2}+\frac{1}{2}\frac{m}{2}\left(u_{1}^{-}\right)^{2}+\frac{1}{2}\frac{1}{12}\frac{m}{2}\left(\frac{l}{2}\right)^{2}\left(\omega_{1}^{+}\right)^{2}+\frac{1}{2}\frac{1}{12}\frac{m}{2}\left(\frac{l}{2}\right)^{2}\left(\omega_{1}^{-}\right)^{2}=\\ & = & \frac{1}{4}m\left[\left(u_{1}^{+}\right)^{2}+\left(u_{1}^{-}\right)^{2}\right]+\frac{1}{192}ml^{2}\left[\left(\omega_{1}^{+}\right)^{2}+\left(\omega_{1}^{-}\right)^{2}\right]\text{.} \end{eqnarray*}\]

Teraz už len stačí dať nájdené výrazy do rovnosti, čím dostaneme tri spomínané zákony zachovania, a potom už len tieto rovnice vyriešiť. My si ale počítanie uľahčíme tým, že riešenie uhádneme.

Predstavme si paličku ako objekt pozostávajúci z malých kúskov, ktoré sa pevne držia za ruky tak, že sa palička ako celok javí byť tuhá. Rozpadnutie paličky potom zodpovedá tomu, že sa dva dieliky uprostred pustia. Je jasné, že tým nevykonajú žiadnu prácu a nijako tým neovplyvnia ostatných susedov – teda nie aspoň v prvom momente po pustení. To znamená, že každý dielik si zachová svoju okamžitú rýchlosť.

Ponechajme označenie ako doteraz a zaveďme označenie pre okamžitú rýchlosť dielika vo vzdialenosti \(r\) od stredu paličky \[ v_{0}^{+,-}\left(r\right)=u_{0}\pm\omega_{0}r\text{.} \] Po rozpadnutí paličky sa ťažiskom polovičky stáva dielik, ktorý bol vo vzdialenosti \(r=\frac{l}{4}\), preto \[ u_{1}^{+,-}\equiv v_{0}^{+,-}\left(\frac{l}{4}\right)=u_{0}\pm\omega_{0}\frac{l}{4}\text{.} \] Okamžitá rýchlosť dielika, ktorý je teraz vo vzdialenosti \(r\) od stredu polovičky paličky, ktorá smerovala pri rozpade nadol, sa dá vyjadriť ako \[ v_{1}^{+,-}\left(r\right)=u_{1}^{+}\pm\omega_{1}r=u_{0}+\omega_{0}\frac{l}{4}+\omega_{1}r\text{.} \] Povedali sme ale, že pri rozpade sa nemení okamžitá rýchlosť jednotlivých dielikov, preto musí platiť napríklad pre koniec paličky \[\begin{eqnarray*} v_{0}^{+}\left(\frac{l}{2}\right) & = & v_{1}^{+}\left(\frac{l}{4}\right)\text{,}\\ u_{0}+\omega_{0}\frac{l}{2} & = & u_{0}+\omega_{0}\frac{l}{4}+\omega_{1}\frac{l}{4}\text{,}\\ \omega_{0} & = & \omega_{1}\text{.} \end{eqnarray*}\]

Dopracovali sme sa k záveru, že pri rozpade sa uhlová rýchlosť paličky zachováva, teda možno značiť \(\omega_{0}=\omega_{1}\equiv\omega\), a že translačné rýchlosti ťažísk polovičiek paličky sú \(u_{1}^{+,-}=u_{0}\pm\frac{1}{4}\omega l\). Dosadením tohto riešenia do zákonov zachovania sa ľahko môžeme presvedčiť o tom, že naše úvahy boli správne.

Keď už teraz vieme, ako sa správa palička pri delení, môžeme pristúpiť k analýze pádu paličky. Ako \(v_{i}\) budeme značiť rýchlosť ťažiska polovice kúsku paličky počas \(i\)-teho delenia a \(s_{i}\) bude dráha, ktorú polovička kúska paličky smerujúca nadol urazí po \(i\)-tom delení za jednu periódu \(\tau=\frac{2\pi}{\omega}\).

Začnime tým, že sa pozrieme na to, ako sa vyvíja rýchlosť \(v_{i}\). Pri prvom delení má ťažisko polovičky smerujúcej nadol rýchlosť \[ v_{1}=\frac{1}{4}\omega l\text{.} \] Následne táto polovička zrýchľuje so zrýchlením \(g\) po dobu \(\tau\) , kedy dôjde k ďalšiemu deleniu. V momente delenia má tentu kúsok paličky rýchlosť \(v_{1}+g\tau\) a polovička tohto kúska smerujúca nadol bude mať po delení rýchlosť \[ v_{2}=v_{1}+g\tau+\frac{1}{8}\omega l\text{.} \] Toto sa opakuje znovu a po ďalšom delení bude mať polovička smerujúca nadol rýchlosť \[ v_{3}=v_{2}+g\tau+\frac{1}{16}\omega l\text{.} \] Ľahko vieme odpozorovať rekurentný vzťah \[ v_{i}=v_{i-1}+g\tau+\frac{1}{2^{i}}\frac{1}{2}\omega l\text{.} \] Opakovaným vnáraným dosádzaním tohto vzťahu vieme nájsť vzťah pre rýchlosť po \(n\)-tom delení \[ v_{n} = \left(n-1\right)g\tau+\frac{1}{2}\omega l\sum_{i=1}^{n}\left(\frac{1}{2}\right)^{i}=\left(n-1\right)g\tau+\frac{1}{2}\omega l\left(1-2^{-n}\right). \]

Pozrime sa teraz na dráhy \(s_{i}\), ktoré urazí kúsok paličky medzi jednotlivými deleniami. Ide zrejme o zvislý vrh nadol, preto \[ s_{i}=v_{i}\tau+\frac{1}{2}g\tau^{2}\text{.} \] Využijúc nájdený vzťah pre rýchlosť paličky po \(n\)-tom delení, vieme ľahko vyjadriť dráhu, ktorú prejde kúsok paličky po tomto delení do ďalšieho v poradí \[ s_{n}=\left(n-\frac{1}{2}\right)g\tau^{2}+\frac{1}{2}\omega l\left(1-2^{-n}\right)\tau\text{.} \]

Teraz už môžeme dopočítať, akú celkovú dráhu prejde najrýchlejší dielik paličky po \(N\) deleniach do \(\left(N+1\right)\)-ho delenia \[\begin{eqnarray*} s & = & \sum_{n=1}^{N}s_{n}=\sum_{n=1}^{N}\left[\left(n-\frac{1}{2}\right)g\tau^{2}+\frac{1}{2}\omega l\left(1-2^{-n}\right)\tau\right]=\\ & = & g\tau^{2}\sum_{n=1}^{N}n+\sum_{n=1}^{N}\frac{1}{2}\tau\left(\omega l-g\tau\right)-\frac{1}{2}\omega l\tau\sum_{n=1}^{N}2^{-n}=\\ & = & \frac{1}{2}N\left(N+1\right)g\tau^{2}+\frac{1}{2}N\omega l\tau-\frac{1}{2}Ng\tau^{2}-\frac{1}{2}\omega l\tau\left(1-2^{-N}\right)=\\ & = & \frac{1}{2}g\tau^{2}N^{2}+\frac{1}{2}\omega l\tau N-\frac{1}{2}\omega l\tau\left(1-2^{-N}\right)\text{.} \end{eqnarray*}\] Využijúc \(\omega\tau=2\pi\) možno tento výraz ešte zjednodušiť na tvar \[ s=\frac{1}{2}g\tau^{2}N^{2}+\pi lN-\pi l\left(1-2^{-N}\right)\text{.} \]

My potrebujeme zistiť, ku koľkým rozpadnutiam dôjde, než prvý dielik dopadne na zem. Matematicky vyjadrené, potrebujeme nájsť najväčšie celočíselné riešenie nerovnice \[ s\left(N\right)=\frac{1}{2}g\tau^{2}N^{2}+\pi lN-\pi l\left(1-2^{-N}\right)\leq H\text{.} \] Táto nerovnica nemá analytické riešenie kvôli prítomnosti člena \(2^{-N}\). Tento člen je však zanedbateľne malý voči \(1\) v prípade, že \(N\gg1\). Vtedy môžeme uvažovať približnú nerovnicu \[ \frac{1}{2}g\tau^{2}N^{2}+\pi lN-\pi l\lesssim H\text{.} \]

V hraničnom prípade platí približná rovnosť \[ N^{2}+\frac{2\pi l}{g\tau^{2}}N-\frac{2\left(\pi l+H\right)}{g\tau^{2}}\approx0\text{.} \]

Jej kladným riešením je \[ N\approx-\frac{\pi l}{g\tau^{2}}+\sqrt{\left(\frac{\pi l}{g\tau^{2}}\right)^{2}+\frac{2\left(\pi l+H\right)}{g\tau^{2}}}. \]

Do momentu, kým dopadne na zem prvý dielik paličky, teda dôjde k \[ N=\left\lfloor -\frac{\pi l}{g\tau^{2}}+\sqrt{\left(\frac{\pi l}{g\tau^{2}}\right)^{2}+\frac{2\left(\pi l+H\right)}{g\tau^{2}}}\right\rfloor \] rozpadnutiam. Pre číselné hodnoty zo zadania to dáva \(N=16\). Vidíme teda, že sme naozaj mohli zanedbať člen \(2^{-N}\) voči \(1\).

Ak by nás zaujímal naozaj celkový počet rozpadnutí, a nie len momentov rozpadnutí, tak si stačí uvedomiť, že pri prvom delení dôjde k jednému rozpadu, pri druhom k dvom, pri treťom k štyrom, atď. To znamená, že celkový počet rozpadnutí vieme nájsť ako \[ M=\sum_{i=1}^{N}2^{i-1}=2^N-1 \] a pre \(N=16\) dostávame \(M=65535\).

Na záver nám zostáva už iba zodpovedať bonusovú úlohu. Predpokladajme, že Adam dokáže paličku rozkrútiť ľubovoľne rýchlo a zamyslime sa nad krajnými prípadmi. Ak by ju rozkrútil príliš pomaly, tak by počet otočení paličky narastal len veľmi pomaly, a teda by aj k deleniu dochádzalo len zriedkavo. Na druhej strane ale aj nárast rýchlosti by bol pomalší, nakoľko príspevok k rýchlosti od rotácie by bol minimálny. No palička zrýchľuje aj vďaka gravitácii, takže ak by perióda otáčania prekročila dobu trvania voľného pádu paličky, k deleniam by už nedochádzalo.

Na druhej strane, ak by Adam roztočil paličku šialene rýchlo, tak by k rozpadom paličky dochádzalo často, čím by aj rýchlosť dielikov rýchlo rástla, takže by pád trval krátko, na napriek tomu by k nejakým otáčkam došlo, pretože tie sú veľmi rýchle. V hraničnom prípade, keby Adam roztočil paličku nekonečne rýchlo, tak by bola polovička paličky hneď vymrštená nekonečnou rýchlosťou, no zároveň by jedna otočka trvala nekonečne krátko. Otázka teda znie, ku koľkým rozpadnutiam dôjde, ak je perióda rotácie šialene malá. Aby sme ju rozlúskli, poďme pracovať s naším výsledkom. Vieme ho upraviť na tvar \[ N=\left\lfloor \frac{\pi l}{g\tau^{2}}\left[\sqrt{1+\frac{2g\tau^{2}\left(\pi l+H\right)}{\pi^{2}l^{2}}}-1\right]\right\rfloor \text{.} \]

Vo výsledku sa nám vyskytuje výraz typu \(\sqrt{1+x}\), ktorý možno pre \(x \ll 1\) aproximovať ako \(\sqrt{1+x}\approx1+\frac{x}{2}\). Pre dostatočne krátke periódy teda platí \[ N=\left\lfloor \frac{\pi l}{g\tau^{2}}\left(1+\frac{g\tau^{2}\left(\pi l+H\right)}{\pi^{2}l^{2}}-1\right)\right\rfloor =\left\lfloor 1+\frac{H}{\pi l}\right\rfloor = 32. \]

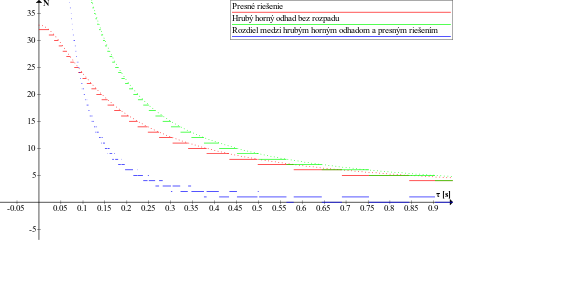
To, ako závisí počet rozpadnutí na perióde otáčania, najlepšie uvidíme na grafe. Červenou je zaznačené naše presné riešenie, zelenou náš prvotný hrubý odhad, no a žltou ich rozdiel. Vidíme, že hrubý odhad diverguje pre krátke periódy, pretože vo vysokofrekvenčnom prípade je práve príspevok k rýchlosti od rotácie dominantným faktorom, no a ten v hrubom odhade nebol započítaný.