2. Starý inventár vzorové riešenie

Zadanie

Kvík v lete brigádoval v prírodovednom múzeu. A veľmi sa mu tam páčilo. Bodaj by aj nie – veď vekovo bol takmer medzi svojimi. Obzvlášť ho zaujali stehenné kosti dinosaurov v zbierke. Chcel ich ukázať aj ostatným vedúcim, no pochopiteľne im ich nemohol priniesť, preto len vyhotovil fotografie a poslal im ich. Povedal im, že sú to kosti velociraptora a T-Rexa, no neprezradil im, ktorá patrí ktorému. „A ktorá je ktorá?“ vyzvedali vedúci, ktorí dobre vedeli, že tyranosaurus bol niekoľkokrát väčší než velociraptor. No ale čo z toho, keď na tých fotkách sú obe rovnako dlhé? „Ste predsa nejakí fyzici! Musíte na to prísť sami.“ odvetil Kvík. A veruže po chvíľke zamyslenia na to aj prišli. Prídete na to aj vy?

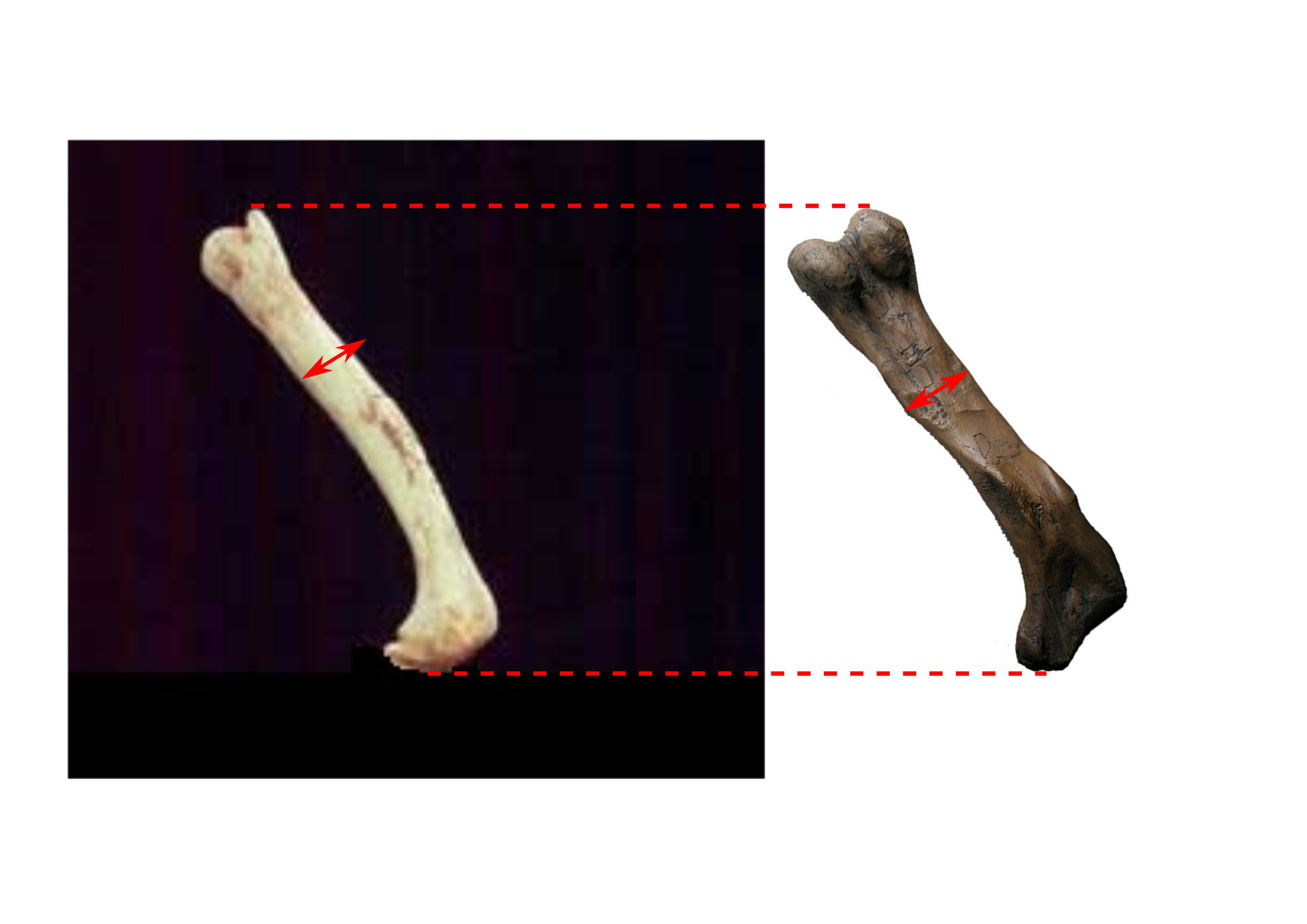
Zistite, ktorá kosť patrí ktorému dinosaurovi. Nezabudnite to odargumentovať po fyzikálnej stránke a svoje argumenty podložte aj matematicky. Môžete predpokladať, že oba dinosaury mali veľmi podobnú stavbu tela. Červené šípky na obrázku majú rovnakú dĺžku. Na záver sa skúste zamyslieť, prečo rozmery kostí presne nesledujú teoretickú predpoveď.

Kľúčom k vyriešeniu tejto úlohy je škálovanie. Zo zadania vieme, že oba dinosaury mali podobnú stavbu tela, preto stehenné kosti oboch jedincov boli zaťažované zhruba rovnako, preto aj ich proporcie by mali byť rovnaké. Z obrázka síce nevieme povedať, ktorá z kostí je väčšia, no vieme určite porovnať pomer dĺžky kosti k jej priemeru \(\frac{l}{d}\). Poďme ho teda preskúmať.

Zaveďme charakteristický rozmer dinosaura \(\lambda\). Potom výška dinosaura \(H\) či jeho dĺžka \(L\) sú úmerné tomuto charakteristickému rozmeru, čiže \(H\propto\lambda\) i \(L\propto\lambda\). Pre nás je dôležité, že i dĺžka kostí je úmerná tomuto charakteristickému rozmeru \(l\propto\lambda\). Hmotnosť \(m\) je zase úmerná tretej mocnine charakteristického rozmeru \(m\propto\lambda^{3}\). Tým pádom i tiaž dinosaura rastie s treťou mocninou charakteristického rozmeru \(F_{G}\propto\lambda^{3}\). To znamená, že s treťou mocninou rozmeru rastie normálová sila \(F_{n}\), ktorou sú v priereze namáhané kosti.

Lenže normálová sila je limitovaná mechanickými vlastnosťami kostí. Pre normálovú silu na základe teórie deformácie pevných látok platí \(F_{n}=\sigma_{n}S\), kde \(\sigma_{n}\) je normálové napätie v kosti a \(S\) je plocha jej prierezu. Maximálna možná normálová sila je daná prierezom kosti a nejakým medzným napätím¹.

Môžeme predpokladať, že dinosaurus dorastá do takej výšky, do ktorej mu to dovoľuje pevnosť jeho kostí daná ich prierezom. Vieme teda, že pevnosť kostí, a teda aj normálová sila rastie s druhou mocninou priemeru² a zároveň s treťou mocninou charakteristického rozmeru, pretože tak rastie tiaž, ktorú musia nohy uniesť. Môžeme teda písať \(F_{n}\propto d^{2}\propto\lambda^{3}\). To ale znamená, že priemer kostí závisí na charakteristickom rozmere ako \(d\propto\lambda^{\frac{3}{2}}\), no a potom \[ \frac{l}{d}\propto\frac{\lambda}{\lambda^{\frac{3}{2}}}=\lambda^{-\frac{1}{2}}\text{.} \]

Nech je charakteristický rozmer T-Rexa \(\lambda_{TR}\) \(k\)-krát väčší než charakteristický rozmer velociraptora \(\lambda_{v}\), čiže \(\lambda_{TR}=k\lambda_{v}\). Vieme, že pomer \(\frac{l}{d}\) je úmerný \(\lambda^{-\frac{1}{2}}\), preto môžeme písať \(\frac{l}{d}=\alpha\lambda^{-\frac{1}{2}}\). Potom zrejme platí \[ \left.\frac{l}{d}\right|_{TR}=\alpha\lambda_{TR}^{-\frac{1}{2}}=\alpha k^{-\frac{1}{2}}\lambda_{v}^{-\frac{1}{2}}=k^{-\frac{1}{2}}\left.\frac{l}{d}\right|_{v}\text{.} \] Vidíme, že pomer dĺžky kosti T-Rexa k jej priemeru má byť \(\sqrt{k}\)-krát menší než u velociraptora.

Uvedomme si, že na jednej fotke je dĺžka i priemer kosti zmenšený rovnako. Tým pádom pomer \(\frac{l}{d}\) na fotke je rovnaký ako v skutočnosti. To isté platí aj pre druhú fotku, no toto zmenšenie je vo všeobecnosti iné než na prvej fotke. Vieme však, že na fotkách \(l_{TR}=l_{v}\). Potom teda pre priemery na fotkách platí \[ d_{TR}=\sqrt{k}d_{v}\text{.} \] Priemer kosti T-Rexa je na fotke \(\sqrt{k}\)-krát väčší než priemer kosti velociraptora, preto kosť T-Rexa je tá s bielym pozadím.

Na záver sa pozrime, či naša analýza zodpovedá skutočnosti. Na internete si nájdeme, akých rozmerov dorastali uvažované dinosaury. Výška T-Rexa bola \(H_{TR}\approx\SI{3.7}{\metre}\) a jeho dĺžka \(L_{TR}\approx\SI{12.3}{\metre}\), výška velociraptora zas \(H_{v}\approx\SI{0.5}{\metre}\) a dĺžka \(L_{v}\approx\SI{2.1}{\metre}\). Ako sme ukázali rozmerovou analýzou, má platiť \[ k=\frac{\lambda_{TR}}{\lambda_{v}}\approx\frac{H_{TR}}{H_{v}}\approx\frac{L_{TR}}{L_{v}}\text{.} \] Pre uvedené hodnoty je hodnota \(k\) niekde okolo \(6\) až \(7\).

Môžeme sa ešte pozrieť, či to sedí aj pre hmotnosti. Hmotnosť T-Rexa \(m_{TR}\) je medzi \(\SI{8.4}{\tonne}\) a \(\SI{14}{\tonne}\), hmotnosť velociraptora \(m_{v}\) medzi \(\SI{15}{\kilo\gram}\) a \(\SI{19.7}{\kilo\gram}\). Keďže \(m\propto\lambda^{3}\), tak \(k\approx\sqrt[3]{\frac{m_{TR}}{m_{v}}}\). To dáva odhad \(k\) niekde medzi \(8\) a \(9\). Je to spôsobené tým, že T-Rex bol predsa len mohutnejší, a preto odhad z hmotností vedie na vyššiu hodnotu \(k\). To je dané tým, že velociraptor bol akýmsi medzičlánkom od dinosaurov ku vtákom, preto jeho telo bolo celkovo ľahšie a zrejme aj kosti boli ľahšie a menej pevné.³

Na záver sa pozrime, ako by mali kosti na fotkách podľa nášho modelu vyzerať. Keďže kosť T-Rexa má mať na fotke \(\sqrt{k}\)-krát väčší priemer, tak podľa toho, aké \(k\) zoberieme, by mala byť zhruba \(\num{2.5}\)- až \(3\)-krát hrubšia než kosť velociraptora. To dokumentuje, že tu náš model zlyháva, aj keď ako rádový odhad je správny. Je to dané hlavne tým, že velociraptor mal ďaleko hrubšie kosti, než by podľa nášho modelu potreboval. Jedným z dôvodov je evolučná stránka – velociraptor je predchodca vtákov, preto jeho telo bolo odľahšené, no kosti zostali hrubé, aj keď nie možno až také pevné. Druhý dôvod je fyzikálny. Také tenké kosti, aké vyšli podľa nášho modelu, by možno dokázali uniesť telo velociraptora, no boli by náchylné na zlomenie ohybom, ktorý sme v našom modeli neuvažovali.

Komentár opravovateľa:

Mnohí ste riešili tento príklad správne, avšak mnohí ste zabudli na matematickú formuláciu vašich záverov. V tomto smere vám Jarov vzorák môže byť výbornou inšpiráciou. Takže do budúcna – nezabúdajte čítať s porozumením :)