6. Biliardové triky vzorové riešenie

Zadanie tohoto príkladu mohlo byť pomerne ťažké interpretovať. Tento vzorák predpokladá nasledujúce:

• medzi guľou a stolom je nulové trenie,
• medzi guľou a tágom zas dostatočne veľké na to, aby sa tágo po guli nemohlo kĺzať
• a tágom do gule udierame v smere rovnobežnom so stolom.

Čo sa teda stane, keď tágom šťuchneme do gule? Impulz, ktorý guľa dostala rozložme na zložku rovnobežnú s povrchom a kolmú na povrch. Sily, pôsobiace v mieste šťuchnutia budú \[ F_\perp = F \cos\alpha \qquad\text{a}\qquad F_\parallel = F \sin\alpha. \] a spôsobia zmenu hybnosti v bode dotyku \[ p_\perp =p \cos\alpha \qquad\text{a}\qquad p_\parallel = p\sin\alpha. \]

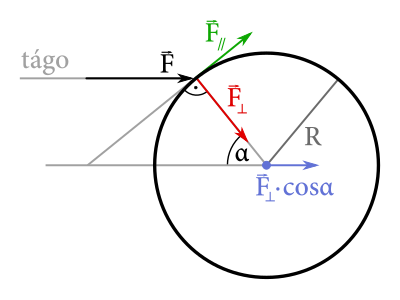
Aby guľa neprešmykovala, musí po šťuchnutí nastať stav, kedy lineárna rýchlosť \(v\) bude ekvivalentná uhlovej rýchlosti \(\omega\), teda \[ v=\omega R. \qquad(1)\]

Lineárnu rýchlosť \(v\) si vieme jednoducho vyjadriť z hybnosti odovzdanej impulzom. K posunu budú prispievať zložky impulzu sily v smere pohybu \[ v = \frac{p_{\perp} }{m} \cos\alpha + \frac{p_{\parallel} }{m} \sin\alpha = \frac{p}{m} \cos^2\alpha + \frac{p}{m} \sin^2\alpha = \frac{p}{m}. \qquad(2)\] K rovnakému výsledku dospejeme jednoducho aj zo zákonu zachovania hybnosti.

Uhlovú rýchlosť získame z momentu hybnosti \(L\). Z definície platí \[ L = R\times p_\parallel \] a pre veľkosť momentu hybnosti \[ \left|L\right| = I\omega. \]

Využijeme, že moment zotrvačnosti gule I je rovný \(\frac{2}{5}MR^2\) a uhlovú rýchlosť \(\omega\) vyjadríme ako \[ \omega = \frac{5p_\parallel}{2mR}=\frac{5p\sin\alpha}{2mR} \qquad(3)\]

Teraz dosadíme rovnice 2 a 3 do rovnice 1 a vyjadríme \(\alpha\) \[ \frac{p}{mR} = \frac{5p\sin\alpha}{2mR} \qquad\Rightarrow\qquad \sin\alpha=\frac{2}{5}. \]

Teda výška nad stredom gule, do ktorej musíme tágom udrieť, bude rovná \[ h = R\sin\alpha = \frac{2}{5}R. \]