Zadanie
O solárnych článkoch sa vraví, že sú ekologickým zdrojom energie budúcnosti. Je to však naozaj tak? Uvažujte vodorovný solárny panel s plochou \(\SI{1}{\square\metre}\) umiestnený niekde na Slovensku. Aký je celoročný priemerný výkon tohoto článku?
Viete, že solárna konštanta je \(\SI[per-mode=symbol]{1360}{\watt\per\square\metre}\).
Solárna konštanta nám vyjadruje tok slnečnej energie prechádzajúcej cez \(\SI{1}{\metre\squared}\) za \(\SI{1}{\second}\) v strednej vzdialenosti Zeme od Slnka. Avšak keď predpokladáme, že Zem je guľatá, vo vyšších zemepisných šírkach nastane situácia, že \(\SI{1}{\metre\squared}\) plochy na povrchu Zeme nebude reprezentovať tok slnečnej energie cez \(\SI{1}{\metre\squared}\). Potrebujeme teda vypočítať zdanlivú plochu solárneho panelu z pohľadu slniečka.
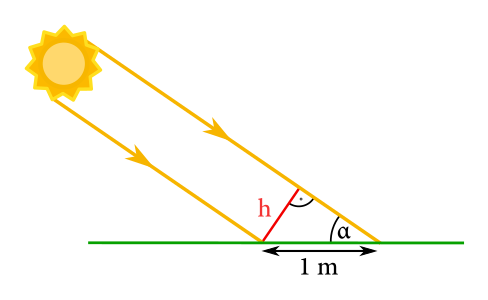
Ako vidíme, zdanlivá výška panelu je \(h = \sin\alpha\). Uhol slnečných lúčov sa počas roka mení a rovnako počet hodín, kedy je slnko na oblohe, preto sa nám hodí spraviť si prieskum, ako tieto hodnoty vyzerajú. Po mesiacoch (za rok 2018) to je:
| mesiac | počet sln. hodín | priemerný uhol sln. lúčov | vykonaná práca [\(\si{\mega\joule}\)] |
|---|---|---|---|
| január | 62 | ||
| február | 93 | ||
| marec | 157 | ||
| apríl | 214 | ||
| máj | 271 | ||
| jún | 286 | ||
| júl | 307 | ||
| august | 284 | ||
| september | 226 | ||
| október | 147 | ||
| november | 71 | ||
| december | 50 |
Práca článku za mesiac \(i\) je rovná \[ W_i = k \cdot h_i \cdot T_i \cdot 3600 = k \cdot \sin \alpha_i \cdot T_i \cdot 3600, \] kde \(k\) je slnečná konštanta a \(T_i\) počet slnečných hodín v danom mesiaci.
Nech \(W\) je súčet prác v jednotlivých mesiacoch. Potom priemerný ročný výkon solárneho panelu bude \[ P = \frac{W}{3600 \cdot 24 \cdot 365} \doteq \SI{251.62}{\watt}. \]
Samozrejme, mohla vám vyjsť aj trochu iná hodnota, závisí od zdroja dát, s ktorými ste pracovali.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.