3. Piestýš vzorové riešenie

Zadanie

Našu úpornú snahu poodhaliť taje termodynamiky sa niekto pokúša zhatiť. Do valca s piestom s plochou \(S\) s \(N\) časticami ideálneho plynu umiestnil pružinu s tuhosťou \(k\) a nulovou pokojovou dĺžkou. Týmto kanadským žartíkom sa však nenecháme odradiť. Ako vyzerajú pre náš plyn jednoduché termodynamické deje (izobarický, izochorický, izotermický a adiabatický) v \(pV\), \(pT\) a \(VT\) diagramoch, kde \(p\) nie je skutočný tlak plynu, ale zdanlivý tlak daný dodatočnou silou, ktorou treba tlačiť piest nadol, aby zostal nehybný?

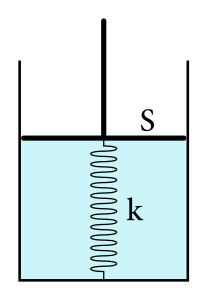
Mary sa prihodilo, že tento kanadský žartík má rozlúsknuť. Najprv zistila, že nulová pokojová dĺžka znamená, že čím je piest vyššie, tým viac sa pružina pokúša ťahať piest nadol, lebo je predĺžená. Teda platí \(F=-k x\).

Ako bude vyzerať stavová rovnica uvažovaná pre náš plyn? Vieme, že pre sily platí \(F_{\mathrm{my}} = F_{\mathrm{plyn}} - F_{\mathrm{pružina}}\). Tieto sily vyjadríme cez príslušné tlaky (plochy sú rovnaké, vykrátia sa): \[ p_{\mathrm{my}} = p_{\mathrm{plyn}} - p_{\mathrm{pružina}}. \]

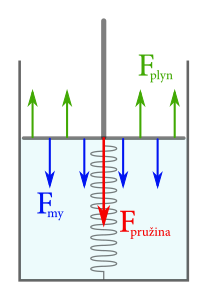
Tlak plynu vyjadríme pomocou stavovej rovnice \(p_{\mathrm{plyn}}=\frac{N k_B T}{V}\). Pre tlak pružiny dostaneme \[ p_{\mathrm{pružina}} = \frac{F}{S} = \frac{-kx}{S} = \frac{-k V}{S^2}. \] Tu sme predĺženie pružiny \(x\) sme vyjadrili ako aktuálnu výšku uzavretej nádoby \(\frac{V}{S}\).

Dosadíme \(p_{\mathrm{plyn}}\) a \(p_{\mathrm{pružina}}\) do rovnice s tlakmi a dostaneme stavovú rovnicu pre náš tlak (odteraz budeme písať \(p \equiv p_{\mathrm{my}}\)): \[ p = \frac{N k_B T}{V} - \frac{-k V}{S^2}. \]

Teraz ju už len treba príslušne upravovať – podľa toho, aký dej prebieha.

Izotermický dej

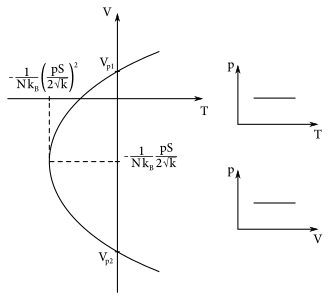
Vidíme, že \(p\) je dané funkciou \(\frac{1}{V}-V\). To je akoby funkcia \(y=\frac{1}{x}-x\). Ľahko určíme priesečník s osou \(V\) – stačí, ak \(p=0\), viď obrázok. Ostatné diagramy sa veľmi líšiť nebudú.

Prečo ide tlak do záporných hodnôt? Je to tlak, akým tlačíme my. Ak je záporný, zodpovedá to zápornej sile a teda v takomto prípade piest ťaháme hore. Nastane to práve vtedy, keď objem plynu je veľký, teda piest je natiahnutý a pružina už priveľmi tlačí späť a túto silu musíme kompenzovať smerom hore. Pri veľkom objeme je i tlak plynu zanedbateľný, pretože zlomok \(\frac{N k_B T}{V}\) bude malý.

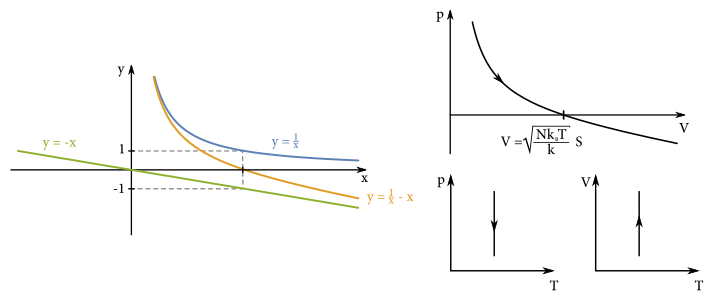
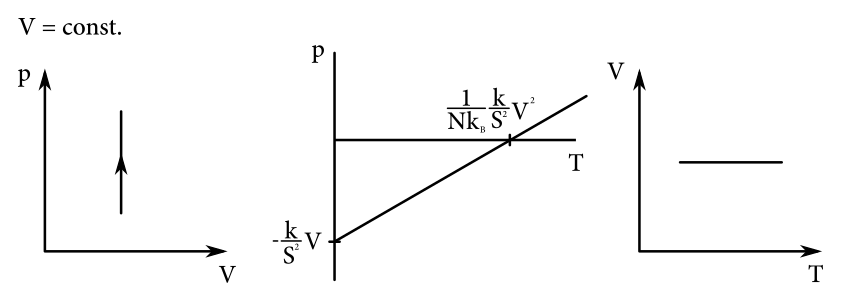
Izochorický dej

\(pV\) a \(VT\) diagramy sú zrejmé. Ešte \(pT\). Vždy pri kreslení diagramov vychádzame zo stavovej rovnice. Vidíme, že \(p\) je úmerné \(T\). Bude to preto akoby lineárna funkcia, avšak posunutá (píšem „akoby“, pretože diagramy nezaznačujú funkcie, ale všetky stavy, v ktorých plyn spĺňa stavovú rovnicu deja). Posunutie začiatku určíme, ak sa pozrieme na prípad \(p = 0\). Dostaneme \[ \frac{N k_B T}{V}=\frac{k V}{S^2}, \] a odtiaľ \[ T = \frac{k V^2}{S^2} \frac{1}{N k_B}, \] čo je bod, kedy je \(p = 0\), a teda je to bod, kde diagram pretína os \(T\). Obdobne, keď položíme \(T = 0\) zistíme, kedy pretne os \(p\), viď graf.

Izobarický dej

Nezabudneme na zadanie, že vždy keď sa hovorí o tlaku, myslí sa tlak, ktorý vyvolávame my. Keďže \(p\) je konštantný, \(pV\) a \(pT\) diagramy sú zrejmé. Avšak \(VT\) diagram treba rozlúsknuť. Ako na to? Je to opäť hra s funkciami. Treba si uvedomiť, že s meniacou sa teplotou sa príslušne bude meniť objem, pretože tlak, ktorým pôsobíme, musí byť konštantný. Budeme sa snažiť nájsť nejakú funkčnú závislosť \(V\) od \(T\), v ktorej \(p\) bude konštanta. Upravíme stavovú rovnicu nasledovne: \[ pV = N k_B T - \frac{k V^2}{S^2}. \]

Po úprave na štvorec dostaneme \[ \left(\frac{p S}{2 \sqrt{k}} + \sqrt{k}\frac{V}{S}\right)^2 - \left(\frac{p S}{2 \sqrt{k}}\right)^2 = N k_B T. \]

Ešte predelíme \(N k_B T\) a z tejto formy vyčítame, kam sa nám posunie začiatok „súradnicovej sústavy“.

Ktoré osi a kde ich diagram pretne? Máme kvadratickú rovnicu: \(\frac{k V^2}{S^2} + p V - N k_B T=0\). Predstavme si to ako funkciu \(x^2\). Vypočítame korene (cez diskriminant) a dostaneme \[ V = -\frac{p}{2 k} \mp \frac{S^2}{2 k} \sqrt{p^2+4 \frac{k N k_B T}{S^2}}. \]

To budú naše priesečníky na „véčkovej osi“, lebo sme to počítali pre \(V\). A máme diagram.