2. Kvíkove nabité gule vzorové riešenie

Zadanie

Kvíkovi pri hre s jeho obľúbenými geomagovými guličkami prišla na um nasledujúca myšlienka – čo keby vo vákuu rozostavil šesť nábojov do tvaru pravidelného šesťuholníka tak, že sa kladný náboj \(q\) a záporný náboj \(-q\) striedajú. Akými smermi by sa tieto náboje začali pohybovať, ak predpokladáme, že v čase \(t = 0\) každý z nich nehybne stál na svojom mieste?

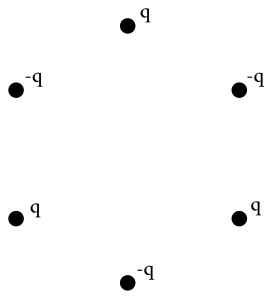
Vieme, že náboje s rovnakými znamienkami sa odpudzujú a náboje s opačnými znamienkami sa priťahujú. Poďme sa teda pozrieť, ako ďaleko by sme zašli len s touto informáciou. V prvom rade si môžeme všimnúť symetriu celého problému. Všetky náboje sú rozmiestnené symetricky do tvaru šesťuholníka a veľkosť ich nábojov je stále rovnaká, mení sa len ich znamienko. Ak sa budeme na situáciu pozerať z pohľadu jedného náboja a potom z pohľadu jeho suseda, musí pre každý z nich nastať rovnaká situácia. Každý náboj má po stranách dva príťažlivé náboje, potom dva odpudivé, a oproti jeden príťažlivý. Takže tá istá symetria bude aj v ich pohybe.

Pozrime sa ďalej, ako sú náboje rozmiestnené. Ak priložíme ku kladnému náboju kladný, odpudia sa a začnú sa pohybovať po priamke na ich spojnici. Sila potom pôsobí vždy smerom rovnobežným so spojnicou dvoch nábojov. V našom hexagóne sa teda zložky síl v smere kolmom na os symetrie prechádzajúcu cez náboj musia vykompenzovať. Výsledkom teda bude, že jediná možnosť je pohyb nábojov v smere do stredu hexagónu alebo od neho.

Aby sme vedeli zodpovedať túto otázku, musíme poznať správanie elektrostatickej sily. V našom prípade vyplýva z Coulombovho zákona \[ F = \frac{-Q_1Q_2}{4\pi\epsilon_0 r^2}, \] ktorý tvrdí, že sila závisí od vzdialenosti nepriamo úmerne druhej mocnine vzdialenosti a priamo úmerne veľkosti nábojov. Platí teda \[ F \propto \frac{Q_1Q_2}{r^2}. \]

Takýto príspevok sily môžeme vektorovo sčítať od každého z nábojov a získame výslednú silu, ktorá pôsobí na skúmaný náboj. Označme zápornú silu ako príťažlivú a dĺžku strany hexagónu \(a\). V našom prípade, ako sme už spomínali, bude jediná nenulová zložka pôsobiť pozdĺž osi symetrie. Jednotlivé vzdialenosti si teda vieme vypočítať z výšky trojuholníka, prípadne uhlov. Pre výslednú silu dostávame \[ \begin{aligned} F_{\mathrm{os}} &\propto 2 \frac{-Q^2}{a^2} \cos\ang{60} + 2\frac{Q^2}{3a^2}\cos\ang{30} + \frac{-Q^2}{4a^2}, \\ F_{\mathrm{os}} &\propto \frac{-Q^2}{a^2}+\frac{Q^2}{3a^2}\sqrt{3}+\frac{-Q^2}{4a^2}, \\ F_{\mathrm{os}} &\propto \frac{Q^2}{a^2}\left(-1+\frac{\sqrt{3}}{3}-\frac{1}{4}\right) < 0. \\ \end{aligned} \]

Aha, dostávame pre výslednú silu zápornú hodnotu. Teda príťažlivá sila bude pôsobiť do stredu hexagónu, čím sa k sebe náboje pritiahnu, ale nezmenia formáciu.