Zadanie
Adam, vyzbrojený svojim ostrovtipom, sa rád prechádza po širokých bratislavských uliciach. Keď ho pri jednej z jeho prechádzok zbadá Jaro, ktorý je často živým terčom jeho vtipov, rozhodne sa pred Adamom radšej schovať. Jediné, čo mu v rýchlosti napadne, je skryť sa za stĺp, ktorý sa nachádza medzi ním a Adamom. Adam sa pohybuje po priamke v kolmej vzdialenosti \(D\) od stĺpa rýchlosťou \(u\). Ako rýchlo sa má pohybovať Jaro po priamke vzdialenej od lampy \(d\), rovnobežnej so smerom Adamovho pohybu, ak nechce byť spozorovaný?
Na začiatok si vyjadrime Adamíkovu rýchlosť \(u\) a Jarovu rýchlosť \(v\): \[ \begin{aligned} u &= \frac{S}{t},\\ v &= \frac{s}{t},\\ \end{aligned} \] pričom \(t\) je nejaký čas, ktorý budú mať oba tvory stále rovnaký. Po vyjadrení \(t\) z oboch rovníc zistíme, že hľadaný čas \(v\) bude vyzerať takto: \[ v = \frac{s}{S}u. \]
Nakreslime si teraz, ako to vyzerá, keď sa Jaro \(J\) skrýva za stĺpom \(T\) pred Adamíkom \(A\).
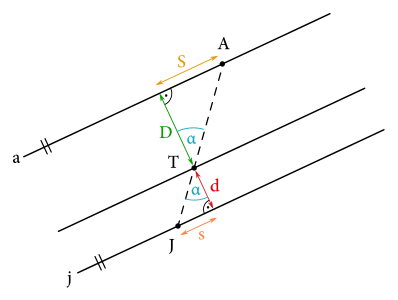
Z obrázka vidíme, že aby Jara \(J\) nebolo za stĺpom vidno, musia ležať body \(J\), \(T\) a \(A\) na jednej priamke. To nám úplne vyhovuje, pretože v tom prípade musia byť uhly \(\measuredangle ATX\) a \(\measuredangle JTY\) stále rovnaké. Z podobnosti trojuholníkov nám potom vyplýva, že \[ \frac{S}{D} = \frac{s}{d} \] a teda \[ \frac{s}{S} = \frac{d}{D}. \]
Po dosadení do prvej rovnice potom vidíme, že chudák Jaro bude musieť udržiavať konštantnú rýchlosť \[ v = \frac{s}{S}u = \frac{d}{D}u. \]
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.