3. Mary a jej väzby vzorové riešenie

Mary si povedala, že väzbová energia sa dá prirovnať práve teplu, ktoré musíme dodať, aby látky prešli z pevného skupenstva (kde je kryštalická mriežka) až po plynné skupenstvo (kde je štruktúra voľná). Prečo?

Dodávaním energie sa ióny v mriežke rozkmitávajú. Mriežka sa začne narúšať. Keď dosiahneme teplotu tesne nad teplotou topenia, tak táto mriežka už neexistuje. Ďalším dodávaním energie sa ióny (teraz už kvapalného skupenstva) rozkmitávajú viac a viac až dosiahnú teplotu varu. Pri ďalšom dodávaní energie sa väzby medzi nimi narúšajú¹, až dosiahneme plynné skupenstvo. A v plynnom skupenstve už častice na seba skoro nepôsobia, preto tento proces môžeme prirovnať rozbíjaniu chemickej väzby. V prípade \(\mathrm{H}_2\mathrm{O}\) ide o van-der-Waalsove väzby medzi molekulami, v prípade \(\mathrm{Na}\mathrm{Cl}\) ide o iónovú väzbu. Pri rozbíjaní chemickej väzby treba dodať také množstvo energie, aby sme vzdialili dva atómy, prípadne ióny natoľko, že nebudú na seba silovo pôsobiť (jednoducho povedané).

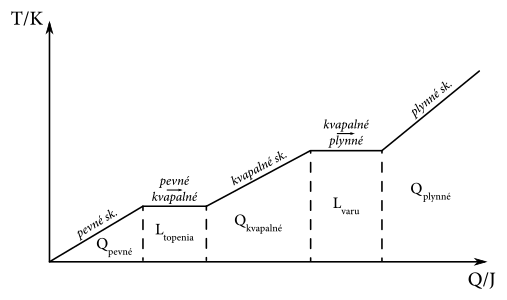
Teda našej Mary treba spočítať všetky teplá, ktoré musí látka prijať aby zvýšila svoju teplotu a menila skupenstvá. Spomenula si na obrázok (viď dole), ktorý nakreslila jej učiteľka na základnej škole. Teda vie, že výsledná energia, ktorú musí dodať látke, bude rovná: teplo potrebné na ohriatie z \(\SI{0}{\kelvin}\) na teplotu topenia + teplo potrebné na zmenu skupenstva z pevného na kvapalné + teplo na ohriatie látky z teploty topenia na teplotu varu + teplo potrebné na zmenu skupenstva z kvapalného na plynné.

Ako prvé spočíta teplá pre \(\mathrm{H}_2\mathrm{O}\), konkrétne teplo potrebné na premenu \(\SI{100}{\gram}\) vody z \(0K\) na teplotu vyparovania. Keďže na výpočet tepla je potrebná hmotnosť vzorky, tak si hmotnosť zvolí a pre ľahkosť výpočtu bude uvažovať \(\SI{100}{\gram}\). Je jedno aké množstvo si zvolí. Aj tak to nakoniec prepočíta na energiu jednej molekuly.

Na zohriatie vody z \(T_0 = \SI{0}{\kelvin}\) na teplotu topenia \(T_t = \SI{273.15}{\kelvin}\) potrebujeme látke v “pevnom” skupenstve dodať teplo \[ Q_p = m \cdot c_p \cdot \left(T_t - T_0\right), \] kde \(m\) je hmotnosť našej vzorky a \(c_p\) je merná tepelná kapacita ľadu. Z tabuliek alebo internetu máme pre \(c_p = \SI{2.05}{\joule\per\gram\kelvin}\). Dostávame \(Q_p = \SI{100}{\gram} \cdot \SI{2.05}{\joule\per\gram\per\kelvin} \cdot \SI{273.15}{\kelvin} \doteq \SI{56}{\kilo\joule}\).

Na skupenský prechod z ľadu na vodu, to je z pevného skupenstva na kvapalné, potrebujeme teplo na roztopenie celej vzorky, ktoré je \(L_t=l_t m\). Z tabuliek máme pre \(l_t=\SI{332.4}{\joule\per\gram}\). Dosadíme a máme \[ L_t = \SI{332.4}{\joule\per\gram} \cdot \SI{100}{\gram} = \SI{33.24}{\kilo\joule}. \]

Na zvýšenie teploty z teploty topenia \(t_t = \SI{273.15}{\kelvin}\) na teplotu varu \(t_v = \SI{373.15}{\kelvin}\) potrebujeme teplo “kvapaliny” \(Q_k = m \cdot c_k \cdot (t_v-t_t)\). Tu je \(c_k\) merná tepelná kapacita látky v kvapalnom skupenstve. Opäť vyhľadáme v tabuľkách mernú tepelnú kapacitu vody. Dostávame \[ Q_k = \SI{100}{\kelvin} \cdot \SI{4.18}{\joule\per\gram\per\kelvin} \cdot \SI{100}{\joule} = \SI{41.8}{\kilo\joule}. \]

Ako posledné potrebujeme látku vypariť, prejsť z kvapalného skupenstva na plynné. Pre teplo potrebné na “vyparenie” platí \(L_v=l_v \dot m\). Merné skupenské teplo vyparovania vody našla na internete, že je \(\SI{40.7}{\kilo\joule\per\mole}\) (až neskôr našla skupenské teplo vyparovania aj v \(\si{\joule\per\gram}\), že je \(l_v = \SI{2259}{\joule\per\gram}\)). Vidí, že má dané merné skupenské teplo vyparovania v hmotnosti na mol. Mary síce nepozná zo školy vzorček (buď nemali alebo si nepamätá). Pozná však trik, že môže urobiť analýzu jednotiek. Navyše, stále má dostatok čokolády, aby rozmýšľala. Urobí takúto úvahu: buď potrebuje dostať hmotnosť do jednotiek \(\si{\gram\per\mole}\) alebo zadanú konštantu do jednotiek \(\si{\joule\per\gram}\) aby jej sedeli jednotky. Rozhodne sa pre druhé, a preto vydelí nájdenú konštantu mólovou hmotnosťou vody a pre teplo dostáva \[ L_v = \SI{100}{\gram} \cdot \frac{\SI{40.7}{\kilo\joule\per\mole}}{\SI{18.00}{\gram\per\mole}} \doteq \SI{226.1}{\kilo\joule}. \]

Teraz všetky teplá sčíta a približne má \[ Q = Q_p + L_t + Q_k + l_v = \SI{56}{\kilo\joule} + \SI{33.24}{\kilo\joule} + \SI{41.8}{\kilo\joule} + \SI{226.1}{\kilo\joule} = \SI{357.14}{\kilo\joule}. \]

Ešte to dostať do jednotiek elektrónvolty. Ako? Vieme, že \(\SI{1}{\electronvolt} = \SI{1.6e-19}{\joule}\). Teda \(\SI{357140}{\joule} = \SI{2.23212e24}{\electronvolt}\).

Mary nezabúda, že výsledok má byť v eV na jednu molekulu. V \(\SI{100}{\gram}\) vody sa nachádza približne \(\SI{5.5}{\mole}\) vody, lebo molárna hmotnosť je \(M_v = \SI{18}{\gram\per\mole}\) (hmotnosť vzorky predelíme molárnou hmotnosťou, ktorá určuje, akú má hmotnosť jeden mol látky a tak dostaneme množstvo látky v móloch). Prenásobením Avogadrovou konštantou dostaneme počet častíc v \(\num{5.5}\) móloch, čo je \(\num{3.3121e24}\) molekúl vody. Už jej len ostáva vydeliť výslednú energiu v \(\si{\electronvolt}\) počtom častíc. Teda \[ \frac{\num{2.23212e24}}{\num{3.3121e24}} \si{\electronvolt} = \SI{0.674}{\electronvolt}. \]

Teda, väzbová energia na jednu molekulu \(\mathrm{H}_2\mathrm{O}\) je približne \(\SI{0.674}{\electronvolt}\)

A teraz rovnaké výpočty urobí pre soľ. Konštaty opäť vyhladá v tabuľkách. Tiež bude uvažovať \(\SI{100}{\gram}\) vzorky. Teplota topenia \(\mathrm{Na}\mathrm{Cl}\) je \(\SI{1075}{\kelvin}\). Na zvýšenie teploty tuhého \(\mathrm{Na}\mathrm{Cl}\) na teplotu topenia potrebujeme teplo \[ Q_p = \SI{100}{\gram} \cdot \SI{0.99}{\joule\per\gram\per\kelvin} \cdot \SI{1075}{\kelvin} \doteq \SI{107.5}{\kilo\joule}. \]

Na zmenu skupenstva z pevného na kvapalné potrebujeme teplo \(\SI{48.2}{\kilo\joule}\). Teplota vyparovania \(\mathrm{Na}\mathrm{Cl}\) je \(\SI{1686}{Kelvin}\). Preto na zvýšenie teploty na teplotu vyparovania potrebujeme \[ Q_k = \SI{100}{\gram} \cdot \SI{1.22}{\joule\per\gram\per\kelvin} \cdot \left(\SI{1686}{\kelvin} - \SI{1075}{\kelvin}\right) \doteq \SI{74.542}{\kilo\joule}. \]

Na zmenu skupenstva z kvapalného na plynné potrebujeme teplo \(L_v=100 \cdot \frac{272600}{58.4} = \SI{466.78}{\kilo\joule}\). Pre celkové teplo dostávame \[ Q = \SI{107.5}{\kilo\joule} + \SI{48.2}{\kilo\joule} + \SI{74.542}{\kilo\joule} + \SI{466.78}{\kilo\joule} = \SI{697.022}{\kilo\joule} = \SI{4.356}{\electronvolt}. \]

Molárna hmotnosť \(\mathrm{Na}\mathrm{Cl}\) je \(\SI{58.44}{\gram\per\mole}\). V \(\SI{100}{\gram}\) \(\mathrm{Na}\mathrm{Cl}\) je približne \(\SI{1.71}{\mole}\), a to je približne \(\num{10.3e23}\) častíc. Teda pre energiu na jednu molekulu dostávame \[ \frac{\num{4.356}}{\num{1.03e24}}\si{\electronvolt}, \] čo je približne \(\SI{4.23}{\electronvolt}\) na jednu molekulu.

Na záver teda máme, že väzbová energia \(\mathrm{H}_2\mathrm{O}\) na jednu molekulu je \(\SI{0.674}{\electronvolt}\). Väzbová energia \(\mathrm{Na}\mathrm{Cl}\) na jednu molekulu je približne \(\SI{4.356}{\electronvolt}\).