2. Otočné dvere? vzorové riešenie

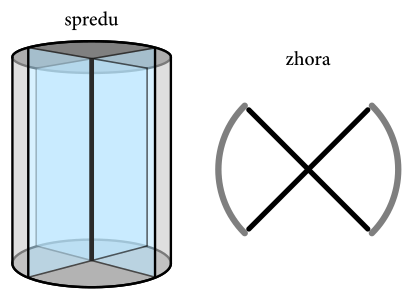
Na začiatok si uvedomíme čo znamená, že dvere sú mechanické. To sú také dvere, ktoré sa neotáčajú pomocou elektriny, ale otočia sa iba ak do nich zatlačíme. Mechanizmov na takéto otočné dvere je vskutku veľa, ale menej z nich bude takých, že sa vrátia do niektorej polohy.

Zamyslime sa teda, aký fyzikálny jav by mal ovplyvniť to, že sa niečo vráti do nejakej polohy. Keďže každý systém sa snaží o to aby mal čo najmenej energie tak by sme sa na to mohli pozrieť cez energie. Vhodným kandidátom je potenciálna energia. Totiž, každé teleso ak mu v tom neni bránené tak sa pokúsi dostať do stavu s menšou potenciálnou energiou. Teda naše dvere by mali mať najmenšiu potenciálnu energiu v jednom zo štyroch stavov a väčšiu inde. Ako niečo takéto docielime? Stačí aby dvere v hociakej polohe okolo vyžadovaných polôh mali možnosť sa voľne presunúť do polohy, ktorá je nižšie a teda aj s menšou potenciálnou energiou.

Konštrukcia: Zavesíme dvere na hnedú obruč tak aby sa vedeli otáčať, napríklad pomocou štyroch koliesok, nad každým krídlom jedno, na koľajnici. Ale obruč nebude len tak hociaká, ale bude mať nasledujúci tvar: \[\begin{align*} x&=r \cdot cos(\phi)\text{,}\\ y&=r \cdot sin(\phi)\text{,}\\ z&=d \cdot cos(4\phi)\text{.}\\ \end{align*}\]

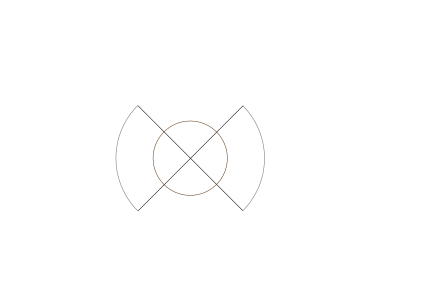
Prvé dve rovnice nám zaručia kružnicu s polomerom \(r\). Tretia nám zaručí, že deformujeme kružnicu tak aby mala naše žiadané vlastnosti. \(d\) zvolíme také aby mala vhodne mierny sklon aby sa dvere dali aj napriek tomu otáčať. Na obrázku 2 je však znázornené \(r=1\), \(d=1\).

Všimnime si, že miesta s najmenšou potenciálnou energiou sú v \(\phi=\frac{\pi}{4} +\frac{k}{2}\pi, k\in \mathbb{N}\) a teda sa dvere vrátia do tejto polohy skoro vždy.

Na záver si treba všimnúť, že existujú miesta \(\frac{k}{2}\pi, k \in \mathbb{N}\) také, že dvere tam zostanú a nevrátia sa do požadovanej polohy, ale keďže sa jedná o labilné stacionárne body, tak za bežných okolností ich do tohto stavu nedostaneme, tj. museli by sme sa naozaj snažiť aby tak zostali stáť. Preto tento špeciálny prípad môžeme mať na vedomí, ale prakticky to výsledok neovplyvní.

Mnohým z vás som dal do komentáru poznámku na zamyslenie, že ako by vyzerali dvere, ktoré majú takú vlastnosť, že sa nevrátia iba do jednej zo štyroch polôh, ale sa vrátia vždy do nasledujúcej. Také dvere vieme skonštruovať napríklad tak, že extrémy, tj. mista s najmenšou a najväčšou potenciálnou energiou, umiestnime blízko seba. To spôsobí, že ak dvere vychýlime v protismere tak sa vrátia ako zvyčajne, ale keď ich vychýlime v smere tak prekonajú extrém a začnú sa pohybovať do nasledujúceho minima. Samozrejme musíme uvažovať veľmi malé zmeny vo výškach, aby sme nespôsobili pasažierovi veľa námahy pri postrčení dverí.