7. Miesič pod tlakom vzorové riešenie

Zadanie

Simon si povedal, že treba zveľaďovať nie len svoje fyzikálne, ale aj fyzické zručnosti. Keď bol naposledy v posilke, stala sa mu ale nemilá nehoda. Precvičoval tam bench press. Na nehmotnú tyč dĺžky \(L\) si naložil závažia s hmotnosťami \(m\). Ľahol si na lavičku, zdvihol tyč a spustil si ju na hrudník. Nasledovať mala fáza, v ktorej tyč so závažiami vytlačí späť nahor… no nenasledovala. Nech sa snažil, ako sa snažil, tyč zostala podopretá v strede o vrchol jeho hrudníka, ktorý sa dá aproximovať polvalcom s polomerom \(R\). Kým pribehli spolucvičiaci a tyč zodvihli, tyč na jeho hrudníku vykonávala kmitavý pohyb. Nájdite periódu malých kmitov tyče.

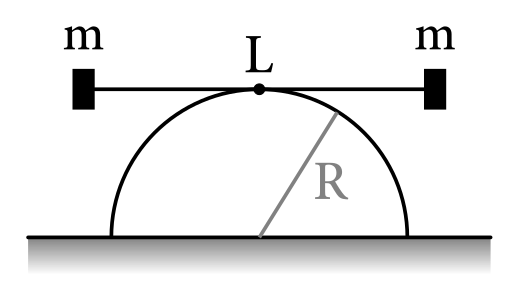
Pre analýzu pohybu činky na mojom hrudníku možno zvoliť niekoľko rôznych prístupov. Jedným z nich je využitie zákona zachovania energie. Energetický prístup sa v tomto príklade ukáže ako drasticky najjednoduchší, preto tu bude prezentovaný práve ten.

Energetický prístup

Ak sa nám podarí vyjadriť celkovú energiu nášho objektu v tvare \[ E = \frac{1}{2}\alpha x^2+ \frac{1}{2}\beta \dot x^2, \]

kde \(x\) je nejaká súradnica a \(\dot x\) je rýchlosť vzhľadom na túto súradnicu, vieme, že objekt vykonáva kmitavý pohyb s periódou \[ T = 2\pi\sqrt{\frac{\beta}{\alpha}}\text{.} \]

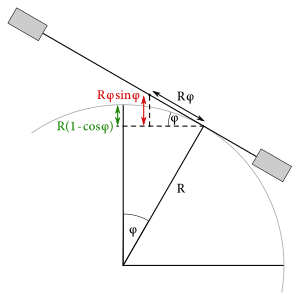
Jednoduché, však? Stačí vyjadriť tú energiu. S tým nám pomôže obrázok. Uhol medzi vertikálou a bodom dotyku činky s hrudníkom sme nazvali \(\phi\). Ťažisko činky je v jej strede a z obrázka ihneď vidno, že potenciálna energia je \[ U=2mg(R\phi\sin\phi-R(1-\cos\phi))\text{.} \]

A teraz kinetická. Tu využijeme vedomosť starých materí, že kinetická energia sa dá vyjadriť viacerými možnými spôsobmi, ktoré sú ekvivalentné a všetky vedú k správnemu výsledku. Napríklad sa vieme pozerať na dve závažia na činke ako dva hmotné body a brať len posuvnú energiu. Alebo ju môžme vyjadriť ako rotačnú energiu okolo ťažiska + posuvná energia ťažiska.

Tretím spôsobom je vyjadriť energiu ako čistú rotáciu okolo okamžitej osi otáčania. Tieto tri spôsoby vždy povedú k správnemu výsledku a líšia sa len jednoduchosťou použitia pre tú-ktorú konkrétnu situáciu.¹ V tomto prípade je najľahší spôsob číslo tri. Okamžitá os otáčania je taká os, ktorá má v danom momente nulovú rýchlosť. V našom prípade je to bod dotyku činky s hrudníkom. A keďže uhol \(\phi\) medzi týmto bodom a vertikálou je rovnaký, ako uhol činky s horizontálou, sú rovnaké aj ich uhlové rýchlosti \(\dot\phi\). Preto je kinetická energia \[ T = \frac{1}{2}I\dot{\phi}^2 = \frac{1}{2}m\left(\left(\frac{L}{2} + R\phi\right)^2 + \left(\frac{L}{2} - R\phi\right)^2\right)\dot{\phi}^2 = m\left(\frac{L^2}{4}+R^2\phi^2\right)\dot{\phi}^2. \]

No a čo teraz? Energia je v tvare aký by sme chceli neni. Sú tam nadbytočné sínusy a kosínusy a tiež je tam člen \(R^2\phi^2\dot{\phi}^2\). Sínusov a kosínusov sa zbavíme ľahko, keďže ich pre malé kmity môžeme aproximovať ako \(\sin\phi\approx\phi\) a \(\cos\phi\approx 1-\frac{\phi^2}{2}\). Ale čo tamten škaredý člen, ako sa ho zbaviť? Môžeme jednoducho povedať, že je neni? Odpoveď je áno. Prečo?

Vieme, že pri kmitavom pohybe sa periodicky energia telesa premieňa z potenciálnej na kinetickú. V maximálnej výchylke má teleso len potenciálnu a pri prechode cez rovnovážnu polohu rovnaké množstvo kinetickej. Pokiaľ sa obmedzíme len na malé výchylky, znamená to, že aj potenciálna energia v maximálnej výchylke je malá a preto je malá aj maximálna možná hodnota kinetickej energie a teda aj rýchlosti! Takže člen rádu \(\phi^2\dot{\phi}^2\) je skutočne zanedbateľný oproti členom rádu \(\phi^2\) alebo \(\dot{\phi}^2\). Ak teda využijeme spomenuté aproximácie, pre celkovú energiu dostávame \[ E \approx mgR\phi^2+m\frac{L^2}{4}\dot\phi^2 \]

a perióda je \[ T = \pi\frac{L}{\sqrt{gR}}\text{.} \]

Poznámka k energetickému prístupu

Prečo to tak funguje? Pre toto: ak napíšeme energiu do tvaru \[ E=\frac{1}{2}\alpha x^2+\frac{1}{2}\beta \dot x^2 \]

a zderivujeme podľa času obe strany rovnice, na ľavej strane zostane nula, keďže energia je v čase konštantná. A na pravej strane \[ \frac{d}{dt}\frac{1}{2}\alpha x^2=\alpha x \dot x, \frac{d}{dt}\frac{1}{2}\beta\dot x^2=\beta\dot x \ddot x\text{.} \]

Teraz \(\dot{x}\) vypadne a dostávame rovnicu harmonických kmitov \[ \alpha x+\beta\ddot x = 0, \] ktorých perióda je samozrejme \(2\pi\sqrt{\frac{\beta}{\alpha}}\).