6. Na druhej koľaji vzorové riešenie

Na prvý pohľad sa mohla zdať táto úloha náročná, keďže v nej vystupujú fotometrické veličiny. V skutočnosti to tak vôbec nie je, uvidíme to, keď sa pozrieme na tieto veličiny trochu bližšie. V jednoduchosti sa dá povedať, že fotometrické veličiny ako svetelný tok alebo osvetlenie vyjadrujú rádiometrické veličiny (tie štandardné, nezávislé na ľudskom vnímaní) preškálovené normovanou citlivosťou oka na jednotlivé vlnové dĺžky. To však znamená, že rovnaké vzťahy, ako platia pri rádiometrických veličinách, budú platiť aj pre fotometrické. Vieme, že vzťah medzi žiarivým výkonom/tokom \(\Phi_e\) a intenzitou ožiarenia/ožiarením \(I_e\) je \[ I_e = \frac{\Phi_e}{S} \cos{\alpha} \text{,} \]

kde \(S\) je plocha, na ktorú dopadá žiarenie, a \(\alpha\) je uhol, ktorý zviera dopadajúce žiarenie s normálou ožiarenej plochy \(S\). Ako bolo povedané, analogický vzťah platí pre svetelný tok \(\Phi\) a osvetlenie \(E\) \[ E = \frac{\Phi}{S} \cos{\alpha} \text{.} \]

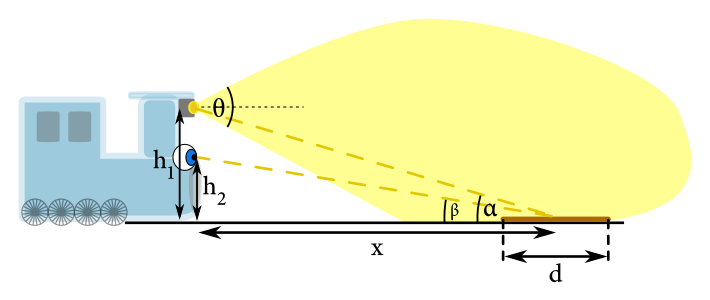
A teraz prejdime k samotnej úlohe. Svetlo z reflektora bude vo vzdialenosti \(r\) dopadať na plochu guľového vrchlíka s obsahom \(2 \pi r^2 \left(1-\cos{\frac{\theta}{2}}\right)\), kde \(\theta\) je vrcholový uhol kužeľa, v našom prípade \(\ang{15}\). Keďže počítame s tým, že plocha prekážky je naozaj malá a prekážka je ďaleko od reflektora, dopadne na ňu iba zlomok svetelného toku, pričom bude závislosť od vzdialenosti zanedbáme. To znamená, že na prekážku dopadne svetelný tok \[ \Phi_2 = \Phi_1 \frac{\pi \left(\frac{d}{2}\right)^2 \sin{\alpha}}{2 \pi r^2 (1-\cos{\frac{\theta}{2}})} \approx \Phi_1 \frac{\pi \left(\frac{d}{2}\right)^2 \frac{h_1}{x}}{2 \pi (h^2_1 + x^2) (1-\cos{\frac{\theta}{2}})} \text{,} \]

kde sme si označili celkový svetelný tok z reflektora \(\Phi_1 = \SI{50000}{\lumen}\), priemer prekážky \(d = \SI{1}{\metre}\), výšku reflektora nad zemou \(h_1 = \SI{3}{\metre}\), horizontálnu vzdialenosť prekážky od Tomáša \(x\), ktorú hľadáme, a uhol, ktorý zviera dopadajúce svetlo s horizontálou \(\alpha \approx \sin{\alpha} \approx \tan{\alpha} = \frac{h_1}{x}\).

Časť tohoto dopadajúceho svetla (konkrétne 10%) prekážka odráža. Zo zadania vieme, že ju odráža rovnomerne do všetkých prípustných smerov (Táto informácia mohla byť pochopená dvoma spôsobmi, a za nepresné zadanie sa teda ospravedlňujeme. Prvá možnosť je, že svietivosť prekážky po odraze je konštantná, a teda nezávislá od uhla, pod ktorým prekážku pozorujeme. Inak povedané prekážka sa správa ako bodový zdroj. S takýmto predpokladom pokračujeme aj vo vzoráku, keďže väčšina riešiteľov to takto pochopila. Druhá možnosť bola pokladať prekážku naozaj za fyzakálne správne matné teleso. Vtedy je konštantná luminancia/jas a predpokladáme lambertovský rozptyl.), čiže do priestorového uhla \(\SI{2 \pi}{\steradian}\) zodpovedajúceho polpriestoru. Teraz už triviálne určíme osvetlenie vo vzdialenosti očí od prekážky ako \[ E = \frac{\num{0.1} \Phi_2 \cos{\beta}}{2 \pi (h^2_2 + x^2)} \approx \num{0.1} \Phi_1 \frac{\left(\frac{d}{2}\right)^2 \frac{h_1}{x}}{4 \pi (h^2_1 + x^2)(h^2_2 + x^2)(1-\cos{\frac{\theta}{2}})}, \]

kde sme označili výšku Tomášových očí od zeme \(h_2 = \SI{2}{\metre}\), a uhol medzi dopadajúcim svetlom do očí a normálou k očiam \(\beta\). Uhol \(\beta\) je veľmi malý, preto sme spravili aproximáciu \(\cos{\beta} = 1\).

Teraz máme rovnicu piateho rádu pre \(x\). Máme dve možnosti. Buď priamo dosadíme do rovnice a dáme ju vyriešiť nejakému múdremu programu, napríklad Wolframu, a dostaneme \(x \doteq \SI{128.37}{\metre}\), alebo si povieme, že \(x \gg h_1, h_2\) a tieto príspevky v súčtoch s \(x\) zandbáme. Potom možno výsledok vyjadriť ako \[ x = \left(\frac{\num{0.1} \Phi_1}{E}\frac{\left(\frac{d}{2}\right)^2 h_1}{4 \pi\left(1-\cos{\frac{\theta}{2}}\right)}\right)^{1/5} \doteq \SI{128.39}{\metre}. \]

Ako môžeme vidieť, táto aproximácia výsledok prakticky nezmenila a bola teda oprávnená. Zostáva nám ešte overiť, či takáto situácia môže nastať, a či naozaj reflektor v takejto vzdialenosti osvetlí prekážku. Keďže však platí, že \(\arctan{\frac{h_1}{x}} < \frac{\theta}{2}\), žiadna patológia nenastane a výsledok je správny.

Väčšina z vás počítala, že prekážka je kolmá smerom k zemi. To spôsobí iba jedinú vec, faktor \(\sin{\alpha}\approx\frac{h_1}{x}\) sa zmení na \(\cos{\alpha} \approx 1\), takže bude treba riešiť rovnicu \[ E = \frac{\num{0.1} \Phi_2 \cos{\beta}}{2 \pi (h^2_2 + x^2)} \approx \num{0.1} \Phi_1 \frac{\left(\frac{d}{2}\right)^2 } {4 \pi (h^2_1 + x^2)(h^2_2 + x^2)(1-\cos{\frac{\theta}{2}})}. \]